Генераторы случайных чисел

Содержание

1. Генераторы случайных чисел
2. Вероятность. Случайные величины с дискретным и непрерывным распределениемПолучение и тестирование случайных чиселПреобразование случайных величин
3. Несколько определенийСобытия называются несовместными, если появление одного
4. Непрерывная и дискретные случайные величины Случайная величина
5. Генератор случайных чисел должен удовлетворять набору жёстких
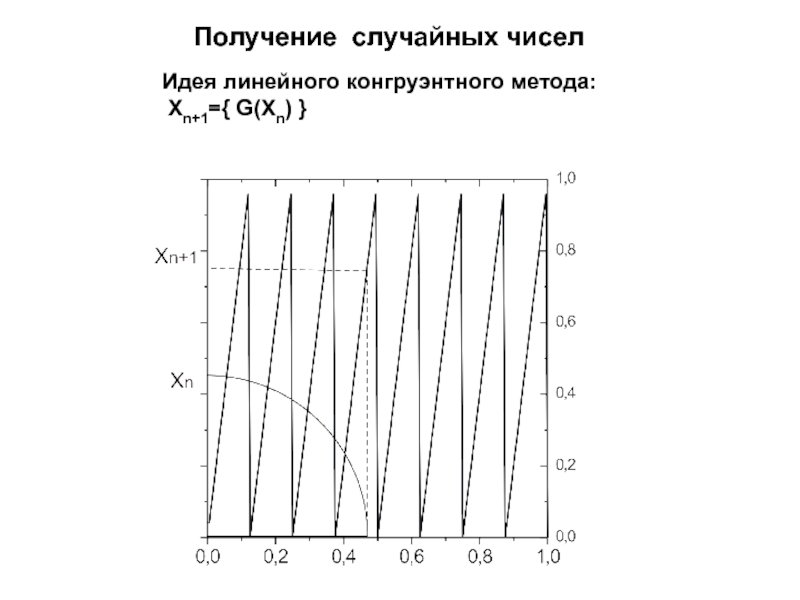
6. Идея линейного конгруэнтного метода: Xn+1={ G(Xn) } Получение случайных чисел
7. Получение случайных чиселЛинейный конгруэнтный методГде а –
8. Линейный конгруэнтный методПреимущества:быстрота, за счет малого количества
9. Генератор Лемера (Lehmer)MINSTD (Park–Miller)a = 75 =
10. Минимальный генератор Парка‑Миллера (Miller “Minimal Standard” generator
11. Алгоритм Шраге (Schrage)При программной реализации MINSTD
12. Получение случайных чисел метод ФибоначчиРекуррентное соотношение:где xk
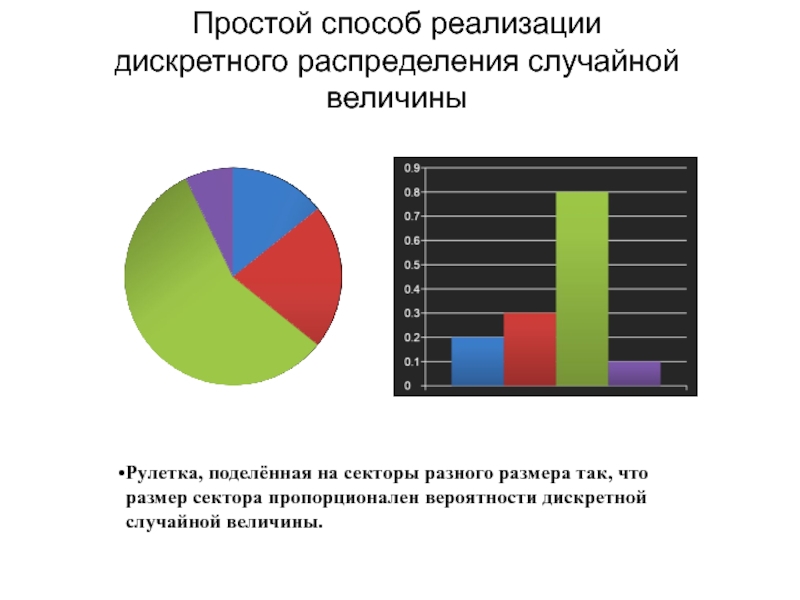
13. Рулетка, поделённая на секторы разного размера так,
14. Разыгрывание непрерывной случайной величины с произвольной плотностью
15. Чтобы разыграть возможное значение нормальной случайной величины
16. Скачать презентанцию

Вероятность. Случайные величины с дискретным и непрерывным распределениемПолучение и тестирование случайных чиселПреобразование случайных величин

Слайды и текст этой презентации

Слайд 1Генераторы случайных чисел

Слайд 2Вероятность. Случайные величины с дискретным и непрерывным распределением

Получение и тестирование

случайных чисел

Преобразование случайных величин

Вероятность. Случайные величины с дискретным и непрерывным распределениемПолучение и тестирование случайных чиселПреобразование случайных величин

Слайд 3Несколько определений
События называются несовместными, если появление одного из них исключает

появление других событий в одном и том же испытании.

Несколько событий

образуют полную группу событий, если в результате каждого испытания происходит хотя бы одно из них.

События образуют полную группу, попарно несовместных событий, если в результате испытания появится одно и только одно из эти событий.

Несколько определенийСобытия называются несовместными, если появление одного из них исключает появление других событий в одном и том

Слайд 4Непрерывная и дискретные случайные величины
Случайная величина называется дискретной, если

принимаемые ею значения можно пронумеровать

Непрерывная случайная величина задаётся

интервалом, содержащим
возможные значения этой величины, и плотностью распределения
вероятности, которая определяется следующим соотношением:

Здесь – (a’,b’) интервал, содержащийся внутри; P (a’<ξ что значение окажется внутри интервала .

Непрерывная и дискретные случайные величины Случайная величина называется дискретной, если принимаемые ею значения можно пронумеровать Непрерывная случайная

Слайд 5Генератор случайных чисел должен удовлетворять набору жёстких требований:

Удовлетворять статистическим тестам

Иметь

как можно более длинный период

Работать как можно быстрее

Воспроизводить одну последовательность

чисел необходимое число раз

Получать одну и ту же последовательность на разных компьютерах.

Генератор случайных чисел должен удовлетворять набору жёстких требований:Удовлетворять статистическим тестамИметь как можно более длинный периодРаботать как можно

Слайд 6
Идея линейного конгруэнтного метода: Xn+1={ G(Xn) }

Получение случайных чисел

Слайд 7Получение случайных чисел
Линейный конгруэнтный метод
Где а – множитель

с – сдвиг
m

– модуль
mod – операция взятия остатка от деления

– начальное значение, «затравка» (seed)

Свойства:
последовательность периодична с периодом, не превышающим m
все элементы этой последовательности однозначно определяются четырьмя параметрами: x0, a, c, m
числа последовательности xn удовлетворяют неравенству xn < m
последовательность чисел yn, равномерно распределенных в интервале (0; 1), получается по формуле

Получение случайных чиселЛинейный конгруэнтный методГде а – множитель с – сдвиг

Слайд 8Линейный конгруэнтный метод
Преимущества:
быстрота, за счет малого количества операций на байт

простота реализации
Недостатки:
предсказуемы
короткий период
некоторые биты «менее случайны», чем другие (обычно это

младшие двоичные разряды)

Линейный конгруэнтный методПреимущества:быстрота, за счет малого количества операций на байт простота реализацииНедостатки:предсказуемыкороткий периоднекоторые биты «менее случайны», чем

Слайд 9Генератор Лемера (Lehmer)
MINSTD (Park–Miller)
a = 75 = 16 807
m =

231 -1 = 2 147 483 647
RANF
a = 75
m =

216 -1 = 65 537

Наиболее популярные:

RANDU
a = 65539
m = 231 = 2 147 483 648

Генератор Лемера (Lehmer)MINSTD (Park–Miller)a = 75 = 16 807m = 231 -1 = 2 147 483 647RANFa

Слайд 10Минимальный генератор Парка‑Миллера (Miller “Minimal Standard” generator - MINSTD)
Не имеет сдвига
Не

требует отсечения «плохих» битов
Простота
Хорошее быстродействие
Хорошее равномерное распределение

Минимальный генератор Парка‑Миллера (Miller “Minimal Standard” generator - MINSTD)Не имеет сдвигаНе требует отсечения «плохих» битовПростотаХорошее быстродействиеХорошее равномерное

Слайд 11Алгоритм Шраге (Schrage)
При программной реализации MINSTD для корректного умножения двух

32-битных чисел по модулю 32-битного числа без переполнения 32-битной переменной

использовался алгоритм Шраге.
Модуль разлагается в выражение:
m=a*q+r
Если rДля вычисления (a*z)(mod m) используется алгоритм:

Для констант Парка-Миллера q=127773 и r=2836.

Алгоритм Шраге (Schrage)При программной реализации MINSTD для корректного умножения двух 32-битных чисел по модулю 32-битного числа

Слайд 12Получение случайных чисел
метод Фибоначчи
Рекуррентное соотношение:
где xk — вещественные числа

из диапазона [0, 1),
a, b — целые положительные числа,

называемые «лагами»

Получение случайных чисел метод ФибоначчиРекуррентное соотношение:где xk — вещественные числа из диапазона [0, 1), a, b —

Слайд 13Рулетка, поделённая на секторы разного размера так, что размер сектора

пропорционален вероятности дискретной случайной величины.
Простой способ реализации дискретного распределения

случайной величины

Слайд 14Разыгрывание непрерывной случайной величины с произвольной плотностью распределения
Чтобы получить

распределение с заданной плотностью p(x) на интервале ( a;b) необходимо

решить уравнение

где y - число из равномерного распределения на интервале (0;1).

Пример: экспоненциальное распределения на интервале (0;x)

что распределено также, как и

Разыгрывание непрерывной случайной величины с произвольной плотностью распределения Чтобы получить распределение с заданной плотностью p(x) на интервале

Слайд 15Чтобы разыграть возможное значение нормальной случайной величины с параметрами σ=1

и а=0, надо сложить 12 случайных чисел из равномерного распределения

на интервале (0,1) и из полученной суммы вычесть 6.

Получение приближённого нормального распределения

Чтобы разыграть возможное значение нормальной случайной величины с параметрами σ=1 и а=0, надо сложить 12 случайных чисел

Скачать презентацию

Разделы презентаций