Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика вокруг нас. Математика в строительстве
Содержание
- 1. Математика вокруг нас. Математика в строительстве
- 2. В истории мы черпаем мудрость, в поэзии остроумие, а в математике – проницательность.Ф. Бэкон
- 3. ЭтимологияСлово «математика» произошло от др.-греч. μάθημα, что
- 4. Математика вокруг насМатематика окружает нас везде. Благодаря
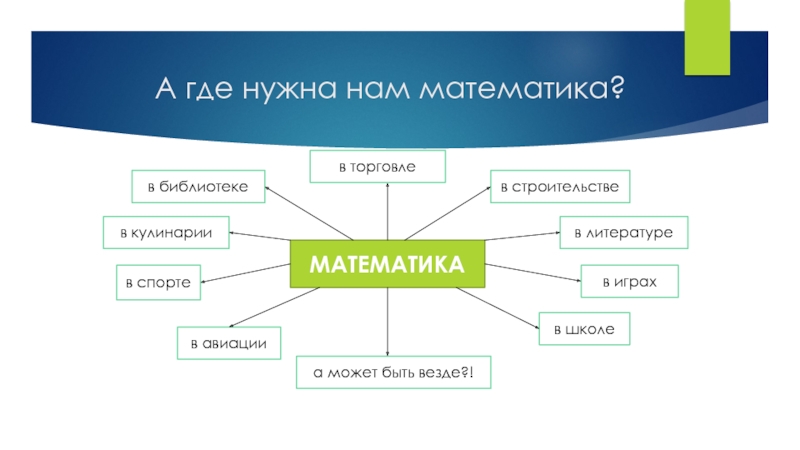
- 5. А где нужна нам математика?МАТЕМАТИКАв торговлев строительствев
- 6. Математика нужна не только в определенных профессиях, но и в повседневной жизни
- 7. В нашей повседневной жизни мы настолько привыкли
- 8. Математика в жизни человекаМногие известные математики говорят,
- 9. Опрос
- 10. Математика вокруг насНапример, наш распорядок дня -
- 11. МАТЕМАТИКА В СТРОИТЕЛЬСТВЕ
- 12. Без знания математики не обойтись при строительстве
- 13. Слайд 13
- 14. Слайд 14
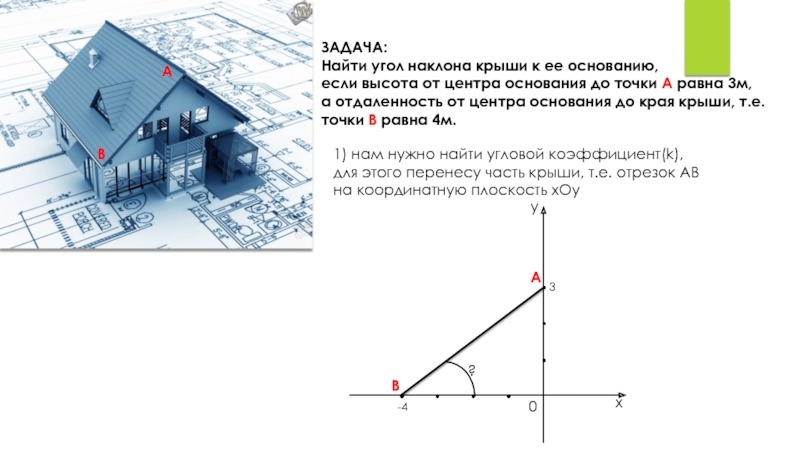
- 15. ЗАДАЧА:Найти угол наклона крыши к ее основанию,если
- 16. 2) теперь мы знаем координаты двух точек:
- 17. В строительстве очень часто возникает потребность в
- 18. Строителю заказали покрасить помещение. Для этого ему
- 19. Необходимо поменять пол для последующей укладки паркета.
- 20. С определением площади нестандартной фигуры сталкиваются в
- 21. Следует отметить, что потребности зарождающегося строительства и,
- 22. Несомненно, и то, что математика, в своем
- 23. Рассмотрев некоторые аспекты применения математики в строительстве,
- 24. ЗАКЛЮЧЕНИЕ Современная жизнь в отсутствии
- 25. СПАСИБО ЗА ВНИМАНИЕ!!!
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Этимология
Слово «математика» произошло от др.-греч. μάθημα, что означает изучение, знание,
наука, и др.-греч. μαθηματικός, первоначально означающего восприимчивый, успевающий, позднее относящийся
к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη, на латыни ars mathematica, означает искусство математики. Термин др.-греч. μᾰθημᾰτικά в современном значении этого слова «математика» встречается уже в трудах Аристотеля (IV век до н. э.). По мнению Фасмера в русский язык слово пришло либо через польск. matematyka, либо через лат. mathematica.Слайд 4Математика вокруг нас
Математика окружает нас везде. Благодаря ней мы решаем
множество вопросов в повседневной жизни. Мало кто задумывался , что
математика окружает нас с первых дней жизни. Любой ребенок, даже не изучавший еще математику, сталкивался с цифрами. В поликлинике узнают наш вес, рост с первых дней жизни. И дальше, всю жизнь мы сталкиваемся с математикой, абсолютно везде.Слайд 5А где нужна нам математика?
МАТЕМАТИКА
в торговле
в строительстве
в играх
в школе
в авиации
в
кулинарии
в спорте
в библиотеке
в литературе
а может быть везде?!
Слайд 7В нашей повседневной жизни мы настолько привыкли к математике, что
даже не замечаем, что пользуемся ею постоянно. А ведь до
сих пор ученики задают вопрос «А зачем нам нужна математика? Только в магазин сходить?». Так для чего же мы изучаем дроби, площадь, периметр, объем? Для чего нужны геометрические сведения? Где каждому человеку математика необходима в повседневной жизни? А что будет, если математику совсем не знать? Необходимо рассмотреть все виды своей деятельности и доказать, что без математики не обойтись в быту.Слайд 8Математика в жизни человека
Многие известные математики говорят, что главное в
математике — научить человека мыслить, ставя порою перед ним очень
сложные задания. «Математика развивает логическое мышление, умение самостоятельно решать проблемы, способность быстро уловить суть и найти к жизненной задаче наиболее подходящий и простой подход»- говорят нам взрослые. Математика тесно связана с нашей повседневной жизнью. Математика встречается в нашей жизни практически на каждом шагу и не такая уж она серая и скучная, а разноцветная и веселая...Слайд 10Математика вокруг нас
Например, наш распорядок дня - режим, не что
иное как определение времени и его планирование в течение дня
при помощи несложных математических вычислений.Мы весь день следим за временем по часам и учимся правильно его распределять, чтобы не опаздывать и не прибегать раньше, чем нужно.
Математика используется и в медицине.
Без математики не обойдутся химические опыты.
Математика используется и для приготовления пищи.
Математика используется в строительстве.
Математика используется практически во всех направлениях.
Слайд 12Без знания математики не обойтись при строительстве или планировании дома,
подсчете затрат на материалы.
Ещё в древности, людям, во время строительства
часто приходилось прибегать к помощи математики.Слайд 14 ЗАДАЧА: Один каменщик выкладывает за 6 рабочих дней 13 м3 кирпича, а
двое учеников(с одинаковой производительностью) на 1 м3 меньше. Найти производительность одного
ученика, если их производительность одинакова. За какое время 5 учеников выложат 75 кубов?РЕШЕНИЕ:
1) (13-1):2= 6(м3) –выкладывает 1 ученик за 6 дней.
2) 6 : 6=1(м3) –производительность 1 ученика.
3) 1 · 5= 5(м3) – 5 учеников за 1 день.
4) 75 : 5 = 15 (дней)
Ответ: за 15 дней 5 учеников выложат 75 кубов кирпича.
Слайд 15ЗАДАЧА:
Найти угол наклона крыши к ее основанию,
если высота от центра
основания до точки А равна 3м,
а отдаленность от центра
основания до края крыши, т.е. точки В равна 4м.1) нам нужно найти угловой коэффициент(k),
для этого перенесу часть крыши, т.е. отрезок АВ на координатную плоскость хОу
А
В
у
х
?
А
В
Слайд 162) теперь мы знаем координаты двух точек: А и В,
от сюда следует, что мы можем составить систему двух линейных
уравнений с двумя переменными, учитывая линейную функцию: y=kx+m.Т.к. А(0;3) и В(-4;0), то получу следующую систему уравнений:
3 = 0 k+m,
0 = -4k+m;
А
В
0
х
у
3
-4
решу систему методом подстановки:
m = 3 (1) - подставлю в (2),
0 = -4k+m (2);
получу: 0=-4k+3,
4k=3,
k= =0,75.
3
4
?