Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мир правильных многогранников
Содержание
- 1. Мир правильных многогранников
- 2. Правильных многогранников вызывающе мало, но этот весьма
- 3. Платон (настоящее имя Аристокл)Днем рождения Платона, которого
- 4. Платоновы тела
- 5. Теория многогранников, в частности выпуклых многогранников, —
- 6. Платоновы тела - трехмерный аналог
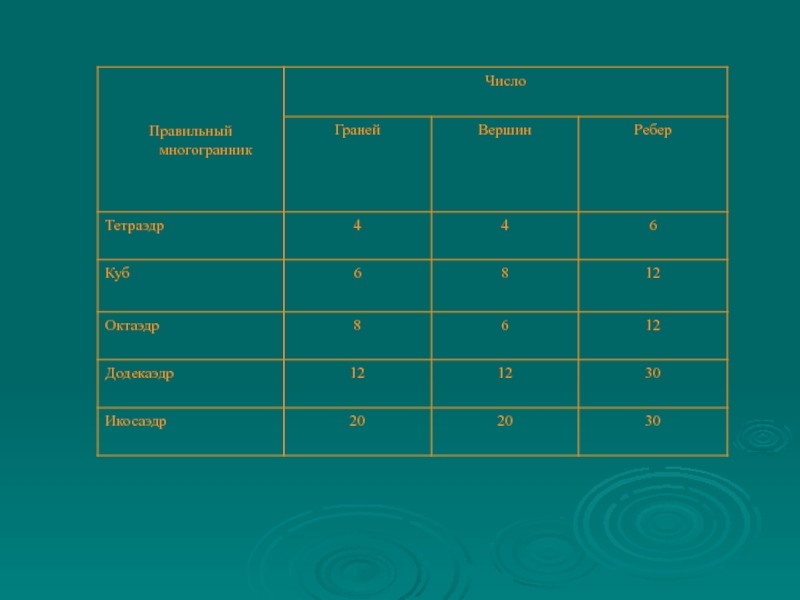
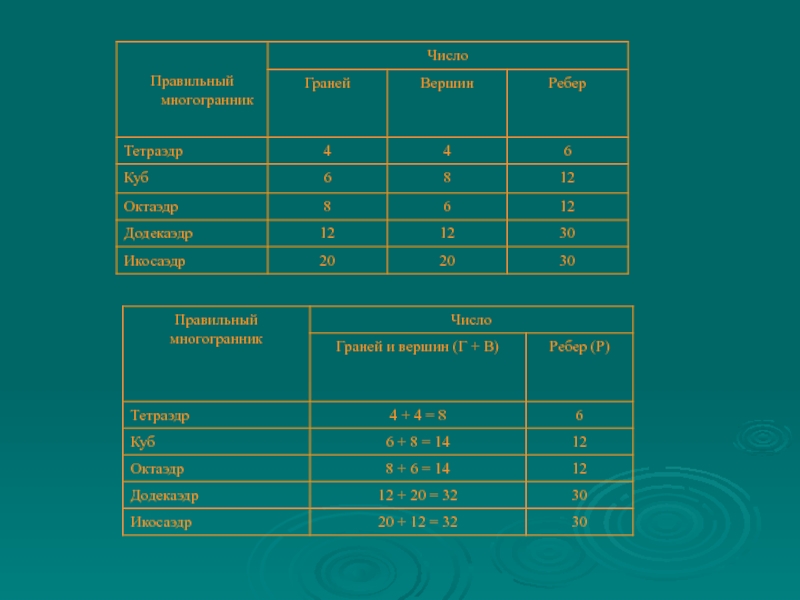
- 7. Правильные многогранникиКуб( гексаэдр)ИкосаэдрОктаэдрДодекаэдрТетраэдр
- 8. Слайд 8
- 9. В мире нет места для некрасивой математики.
- 10. Октаэдр - (от греческого okto – восемь
- 11. Икосаэдр - (от греческого ico — шесть
- 12. Тетраэдр - (от греческого tetra – четыре
- 13. Додекаэдр (от греческого dodeka – двенадцать и
- 14. Слайд 14
- 15. Леонард Эйлер 1707 - 1783
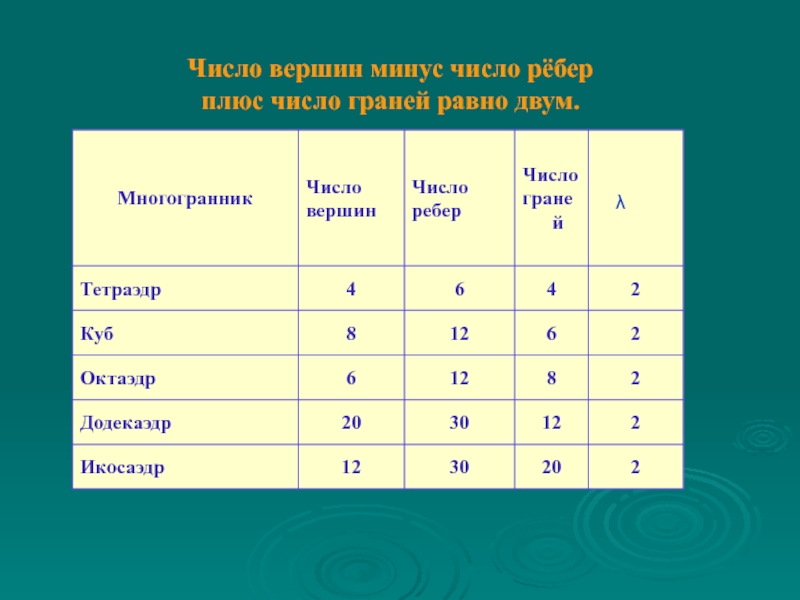
- 16. Пусть В --- число вершин выпуклого многогранника,
- 17. Слайд 17
- 18. Число вершин минус число рёбер плюс число граней равно двум. λ
- 19. Архимедовы тела
- 20. Архимед (ок. 287-212 г. до н. э.)
- 21. Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
- 22. Усеченный тетраэдрКубооктаэдрУсеченный октаэдрУсеченный кубРомбокубооктаэдрУсеченный кубооктаэдрПлосконосый куб Усеченный икосаэдрПлосконосый додекаэдрИкосододекаэдрУсеченный додекаэдрРомбоикосододекаэдрУсеченный икосододекаэдр14. псевдоромбокубоктаэдр
- 23. Иоганн Кеплер (1571-1630) - немецкий астроном и
- 24. Космологическая теория
- 25. Звёздчатые многогранникиМалый звездчатый додекаэдрБольшой звездчатый додекаэдр«стелла октангула»Звездчатый
- 26. Геология
- 27. Слайд 27
- 28. Химия
- 29. 1)Поваренная соль - NaCl2) Li, Na,
- 30. Предмет математики настолько серьезен, что полезно не
- 31. Кристаллы алмаза Кристаллы алмаза обычно имеют форму
- 32. Алмаз «Шах»
- 33. Слайд 33
- 34. Биология Природа говорит языком математики; буквы этого
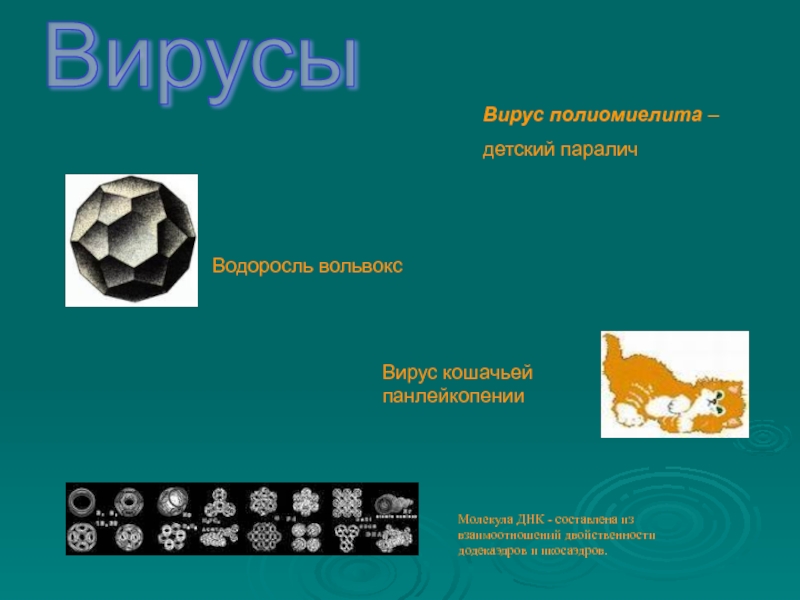
- 35. Вирусы Вирус полиомиелита – детский параличВодоросль вольвоксМолекула
- 36. Искусство
- 37. Во всём мне хочется дойти До самой сути
- 38. Альбрехт Дюрер (1471- 1528) гравюра ''Меланхолия ''.
- 39. Петер Пауль Рубенс (1577-1640)Тайная Вечеря. ЭскизЛеонардо да Винчи. Тайная вечеря.
- 40. Сальвадор Дали
- 41. Слайд 41
- 42. М.К.Эшер Голландский художник Мориц Корнилис Эшер,
- 43. Четыре правильных многогранникаПорядок и хаосЗвезда
- 44. М. Эшер. Ячейки кубического пространстваЛеонардо да Винчи. Упаковка кубовМ. Эшер. гравюры «Водопад»
- 45. Архитектура
- 46. Слайд 46
- 47. Музейно-развлекательный комплекс
- 48. Великая пирамида Хеопс
- 49. Александрийский маяк
- 50. Когда мы стремимся искать неведомое нам, то
- 51. ЛитератураНаучно-популярное издание Энциклопедия для детей. Математика. Издательство «Аванта+»Энциклопедия для детей. Искусство. Издательство «Аванта+»
- 52. Скачать презентанцию
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробиться в самые глубины различных наук.
Слайды и текст этой презентации
Слайд 2Правильных многогранников вызывающе мало, но этот весьма скромный по численности
отряд сумел пробиться в самые глубины различных наук.
Л. Кэролл
Слайд 3Платон
(настоящее имя Аристокл)
Днем рождения Платона, которого еще при жизни
за мудрость называли “божественным”, по преданию считается 7 таргелион (21
мая), праздничный день, в который, согласно древнегреческой мифологии, родился бог Аполлон. Год рождения в различных источниках указывается 429 - 427 до Р.Х.
Слайд 5Теория многогранников, в частности выпуклых многогранников, — одна из самых
увлекательных глав геометрии.
Л. А. ЛюстерникОгонь – тетраэдр
Вода – икосаэдр
Воздух – октаэдр
Земля – куб
Вселенная - додекаэдр
Слайд 6 Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Однако между двумерным и трехмерным случаями есть важное отличие: существует
бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство факта известно уже более двух тысяч лет.
Слайд 9В мире нет места для некрасивой математики.
Готфрид Харди
Куб -самый популярный многогранник из семейства Платоновых тел.
Куб или гексаэдр (от греческого hex — шесть и hedra — грань) составлен из 6 квадратов.
Слайд 10Октаэдр -
(от греческого okto – восемь и hedra –
грань) - правильный многогранник, составленный из 8 равносторонних треугольников.
Октаэдр
имеет 6 вершин и 12 ребер.. 
Слайд 11Икосаэдр -
(от греческого ico — шесть и hedra —
грань)
правильный выпуклый многогранник, составленный из 20 правильных треугольников.
Каждая из 12
вершин икосаэдра является вершиной 5 равносторонних треугольников. У икосаэдра 30 ребер. 
Слайд 12Тетраэдр -
(от греческого tetra – четыре и hedra –
грань) - правильный многогранник, составленный из 4 равносторонних треугольников
Слайд 13Додекаэдр (от греческого dodeka – двенадцать и hedra – грань)
это правильный многогранник, составленный из двенадцати равносторонних пятиугольников.
Додекаэдр имеет
20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников.
Додекаэдр
Слайд 16Пусть В --- число вершин выпуклого многогранника, Р --- число
его рёбер и Г --- число граней. Тогда верно равенство
В-Р+Г=2.Число λ = В – Р + Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2.
Теорема Эйлера
Слайд 20Архимед (ок. 287-212 г. до н. э.) - древнегреческий механик
и математик, родом из Сиракуз (Сицилия).
Вклад Архимеда в теорию
многогранников - описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел). До нашего времени эта работа Архимеда не сохранилась, но ссылки на нее имеются у Паппа.(Папп Александрийский (2-я половина III в. н. э.) - математик, жил и работал в Александрии.) Архимед
Слайд 21
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые
многогранники, все многогранные углы которых равны, а грани - правильные
многоугольники нескольких типов (этим они отличаются от платоновых тел, грани которых - правильные многоугольники одного типа).
Слайд 22Усеченный тетраэдр
Кубооктаэдр
Усеченный октаэдр
Усеченный куб
Ромбокубооктаэдр
Усеченный кубооктаэдр
Плосконосый куб
Усеченный икосаэдр
Плосконосый додекаэдр
Икосододекаэдр
Усеченный додекаэдр
Ромбоикосододекаэдр
Усеченный
икосододекаэдр
14. псевдоромбокубоктаэдр
Слайд 23Иоганн Кеплер (1571-1630) - немецкий астроном и математик. Один из
создателей современной астрономии - открыл законы движения планет (законы Кеплера),
заложил основы теории затмений, изобрел телескоп, в котором объектив и окуляр - двояковыпуклые линзы.Иоганн Кеплер
Слайд 25Звёздчатые многогранники
Малый звездчатый додекаэдр
Большой звездчатый додекаэдр
«стелла октангула»
Звездчатый икосаэдр
Большой икосаэдр
О мир,
пойми! Певцом - во сне - открыты
Закон звезды и формула
цветка!М. Цветаева
Слайд 291)Поваренная соль - NaCl
2) Li, Na, Cr, Pb, Al,
Au
3) Кристалл алмаза
4) Кристаллическая решётка хлорида цезия (CsCl).
Кристаллы
Монокристалл алюмокалиевых квасцов, формула которого K(AL(SO4)2 )*12Н2О. Они применяются для протравливания тканей, выделки кожи.
Куприт (медь рубиновая или красная медная руда), минерал, оксид меди, Cu2O.
Название происходит от лат. cuprum – медь.
Сотри случайные черты и ты увидишь - мир прекрасен!
Слайд 30Предмет математики настолько серьезен, что полезно не упускать случая сделать
его немного занимательным.
Блез ПаскальФуллерена
Метан
Слайд 31Кристаллы алмаза
Кристаллы алмаза обычно имеют форму октаэдра.
Алмаз (от
греческого adamas – несокрушимый) – бесцветный или окрашенный кристалл с
сильным блеском в виде октаэдра. Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, ромбододекаэдров, реже — кубов или тетраэдров.
Слайд 34Биология
Природа говорит языком математики; буквы этого языка - круги
треугольники и другие математические фигуры.
Галилео ГалилейФеодория
Слайд 35Вирусы
Вирус полиомиелита –
детский паралич
Водоросль вольвокс
Молекула ДНК - составлена
из взаимоотношений двойственности додекаэдров и икосаэдров.
Вирус кошачьей панлейкопении
Слайд 37Во всём мне хочется дойти
До самой сути
В работе, в
поисках пути,
В сердечной смуте.
До сущности протекших дней,
До
их причин, До оснований, до корней
До сердцевины...
Б.Л.Пастернак
Слайд 42 М.К.Эшер
Голландский художник Мориц Корнилис Эшер, родившийся в 1898
году в Леувардене, создал уникальные и очаровательные работы, в которых
использованы или показаны широкий круг математических идей1898- 1972
Слайд 44М. Эшер. Ячейки кубического пространства
Леонардо да Винчи. Упаковка кубов
М. Эшер.
гравюры «Водопад»
Слайд 50Когда мы стремимся искать неведомое нам, то становимся лучше, мужественнее
и деятельнее тех, кто полагает, будто неизвестное нельзя найти и
незачем искать. Платон.
Слайд 51Литература
Научно-популярное издание Энциклопедия для детей. Математика. Издательство «Аванта+»
Энциклопедия для детей.
Искусство. Издательство «Аванта+»
