Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники. Призма
Содержание
- 1. Многогранники. Призма
- 2. Многогранники - Теория - Правильные многогранники - Призма
- 3. Многогранники Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое геометрическое тело.
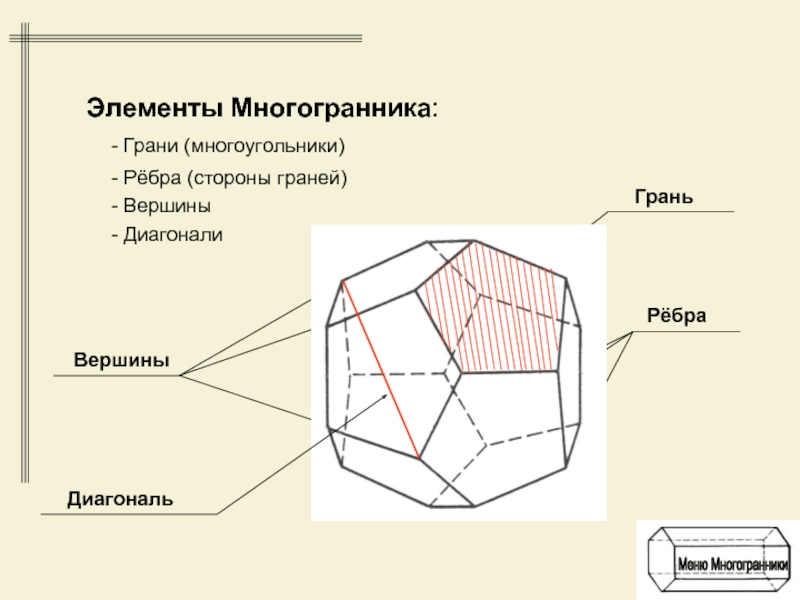
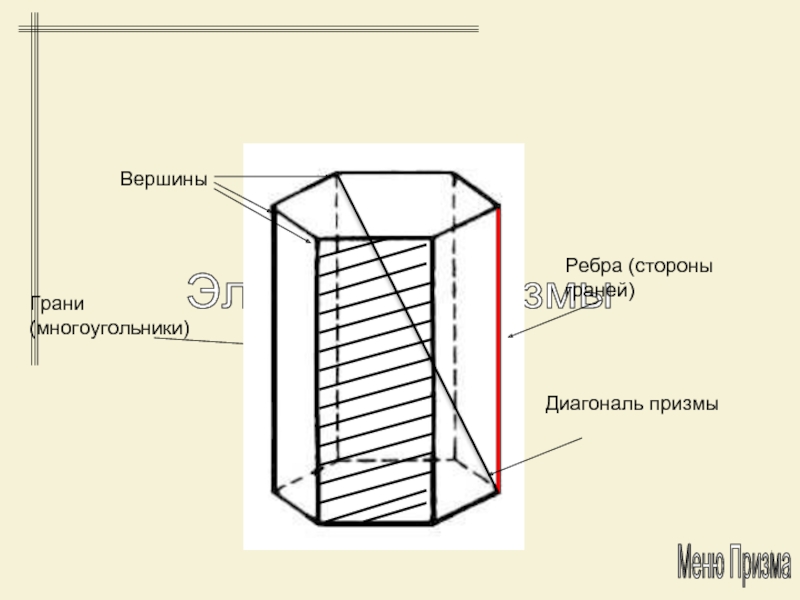
- 4. Элементы Многогранника:- Грани (многоугольники)- Рёбра (стороны граней)- Вершины- Диагонали
- 5. Свойство выпуклого многогранника:Сумма всех плоских углов в
- 6. Многогранник называется правильным, если он:1. Выпуклый2. Все
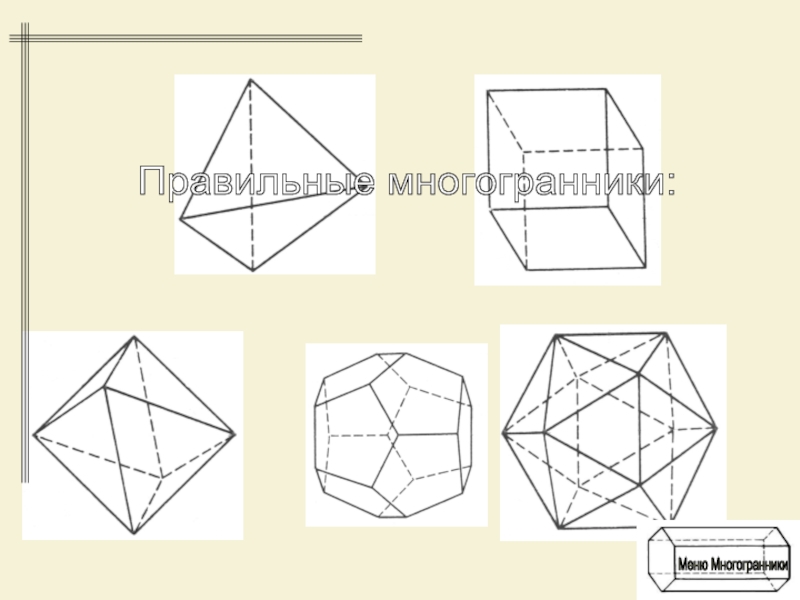
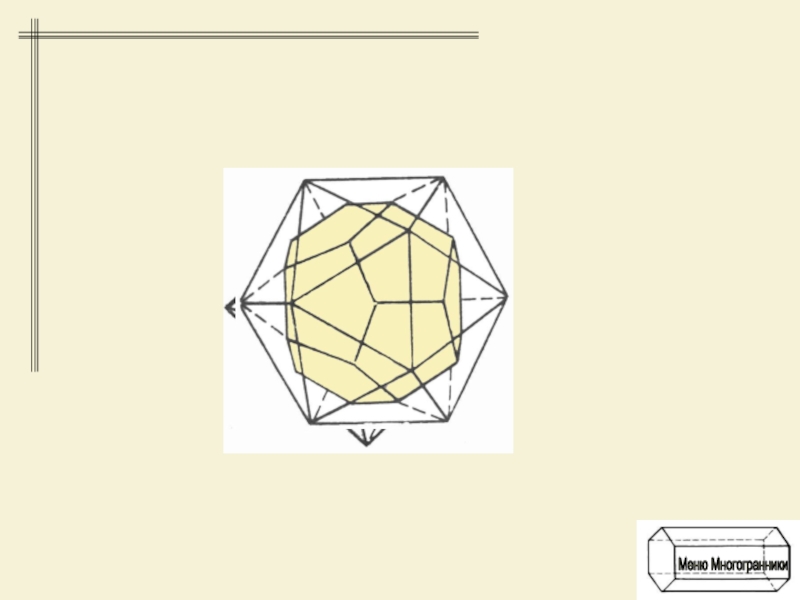
- 7. Правильные многогранники:
- 8. Слайд 8
- 9. Призма - Теория - Элементы - Нахождение площадей - Задачи
- 10. Призма (греч. prísma), многогранник, у которого две
- 11. Элементы призмы Меню Призма
- 12. Высотой (h) призмы называется перпендикуляр ,
- 13. Правильная призма Правильной призмой называется прямая призма, основание которой – правильный многоугольник.Меню Призма
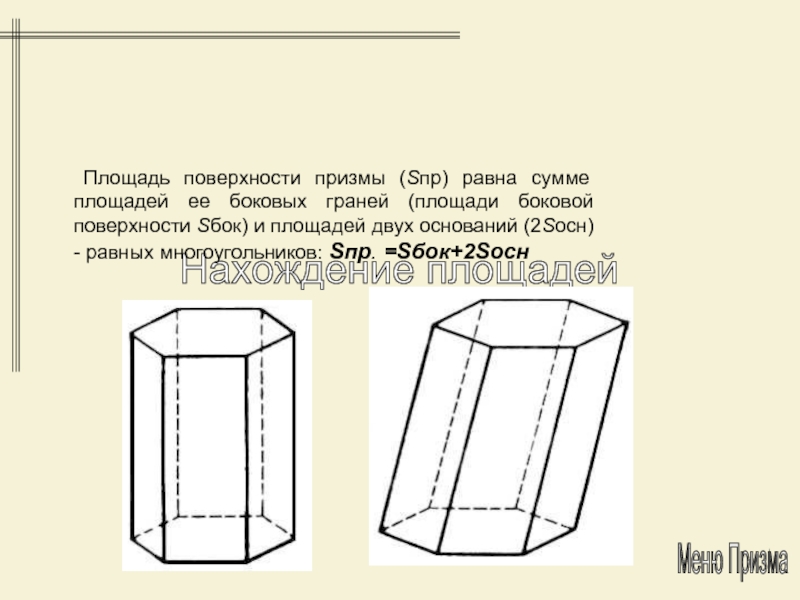
- 14. Нахождение площадей Площадь поверхности призмы (Sпр) равна
- 15. Площадь боковой поверхности – сумма площадей боковых
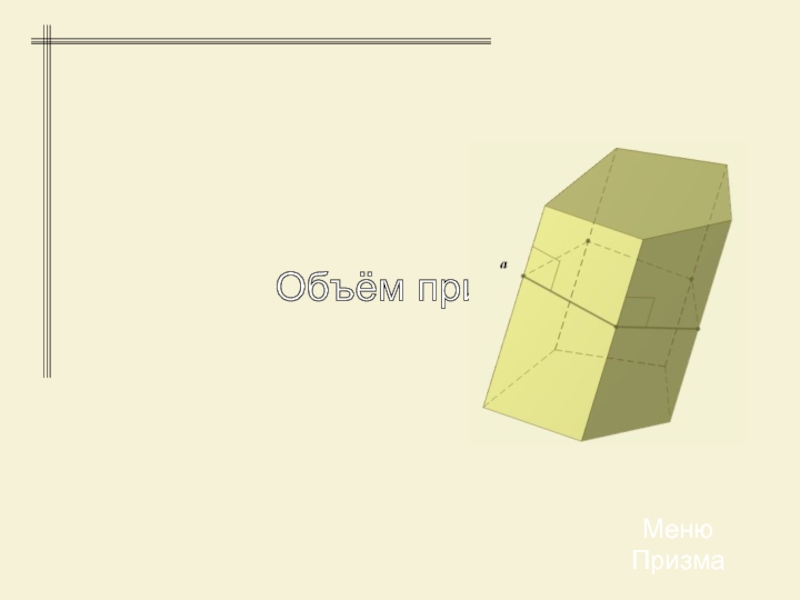
- 16. Объём призмы МенюПризма
- 17. Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.МенюПризма
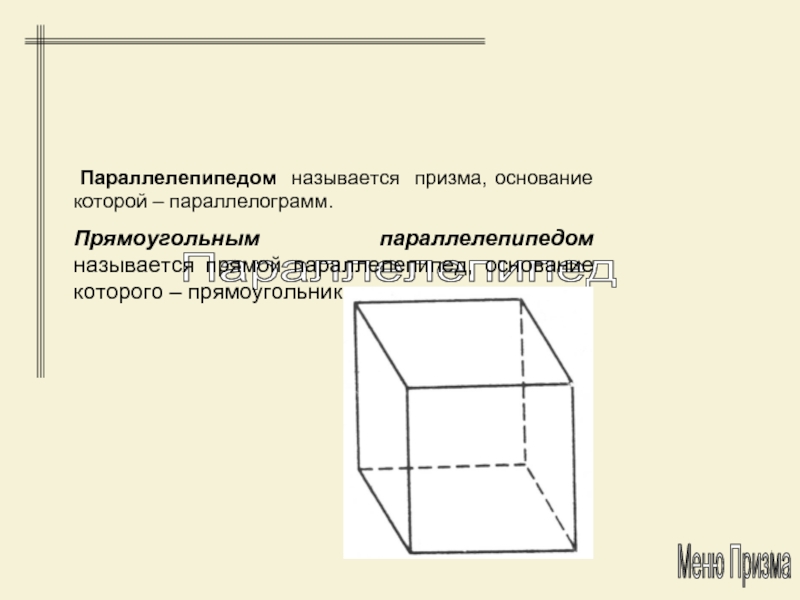
- 18. Параллелепипед Параллелепипедом называется призма, основание которой –
- 19. Свойства параллелепипеда Меню Призма Противоположные грани
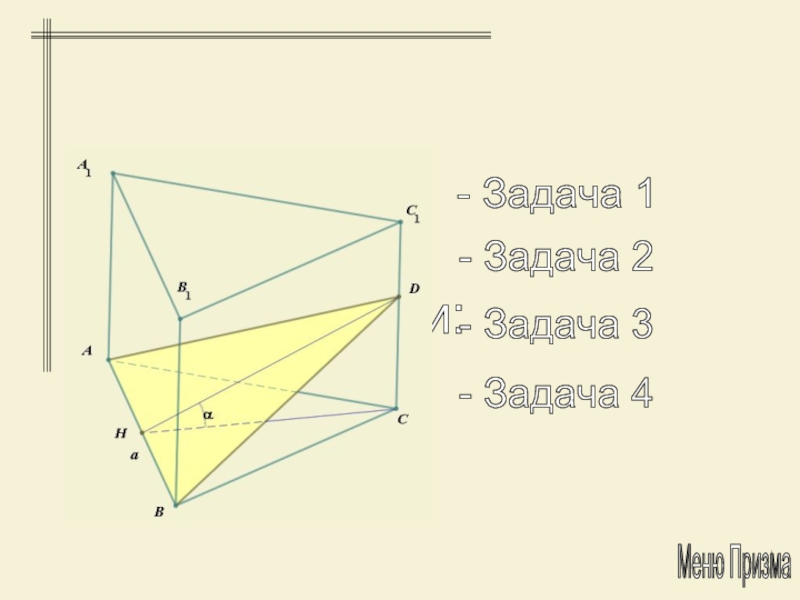
- 20. Задачи: - Задача 1 - Задача 2 - Задача 3 - Задача 4 Меню Призма
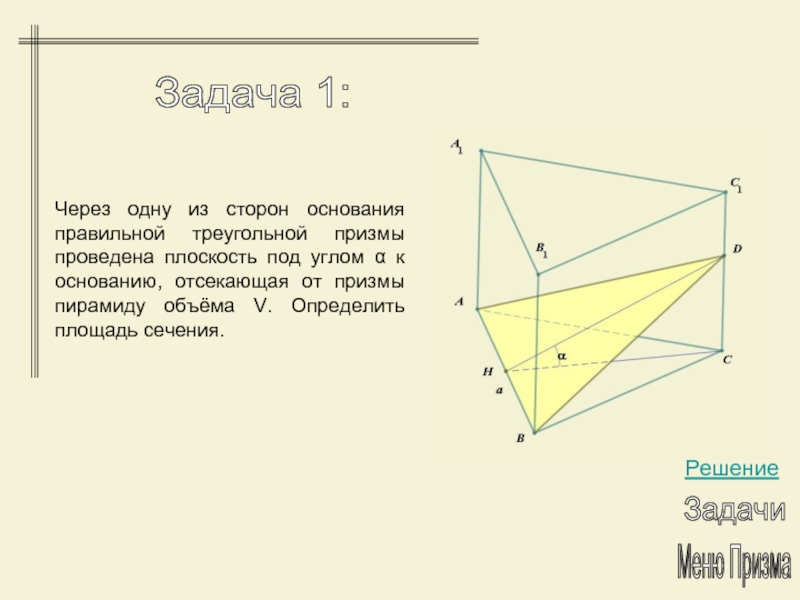
- 21. Через одну из сторон основания правильной треугольной
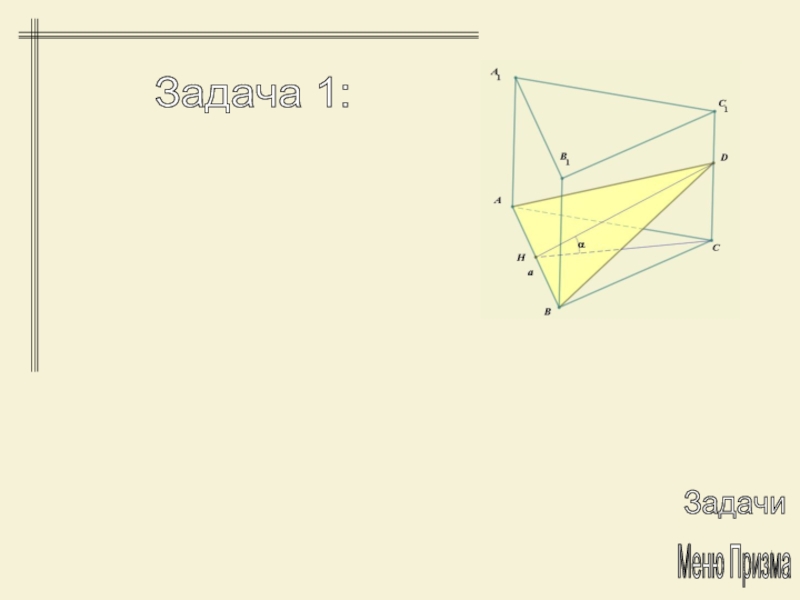
- 22. Задача 1: Меню Призма Задачи
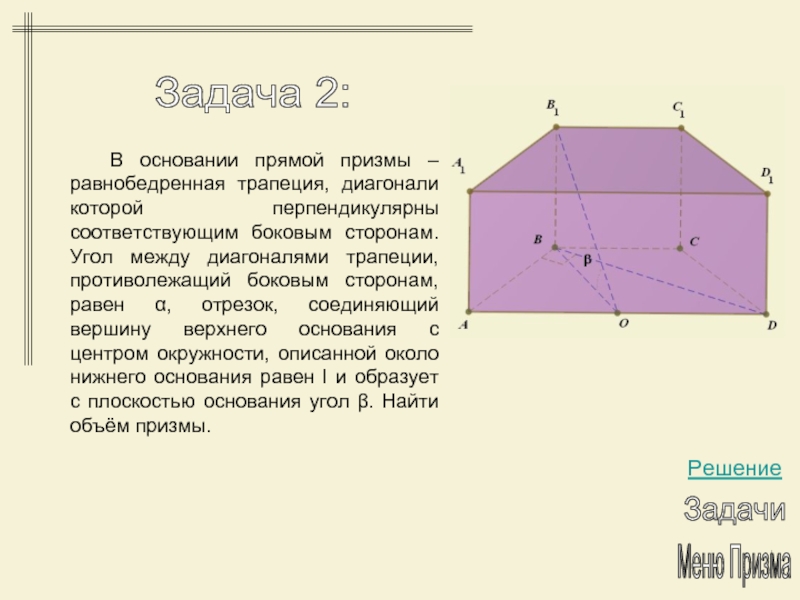
- 23. Задача 2: Меню Призма РешениеЗадачи В основании
- 24. Задачи Меню Призма Задача 2:
- 25. Меню Призма Задача 3: РешениеЗадачи Через середину
- 26. Задачи Меню Призма Задача 3:
- 27. Меню Призма Задача 4: РешениеЗадачи Дана прямая
- 28. Задачи Задача 4: Меню Призма
- 29. Скачать презентанцию
Многогранники - Теория - Правильные многогранники - Призма
Слайды и текст этой презентации
Слайд 3Многогранники
Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое геометрическое
тело.
Слайд 5
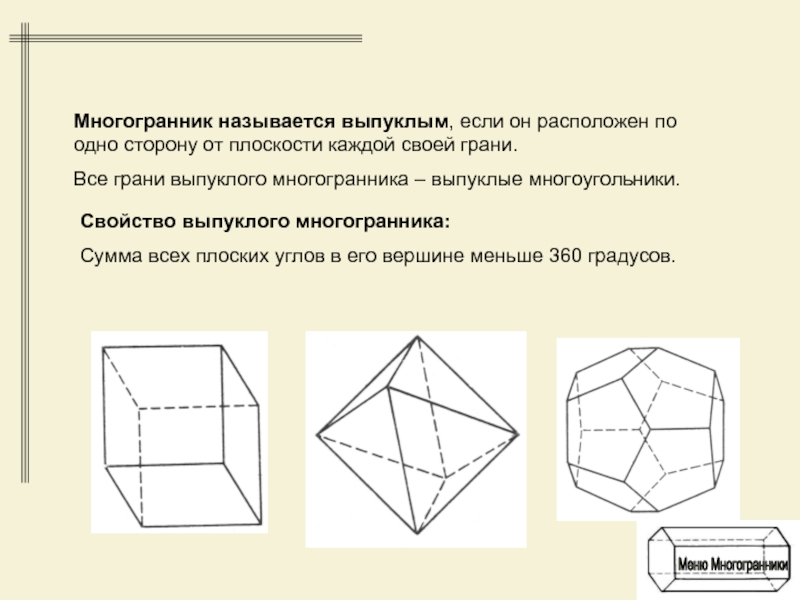
Свойство выпуклого многогранника:
Сумма всех плоских углов в его вершине меньше
360 градусов.
Многогранник называется выпуклым, если он расположен по одно сторону
от плоскости каждой своей грани.Все грани выпуклого многогранника – выпуклые многоугольники.
Слайд 6
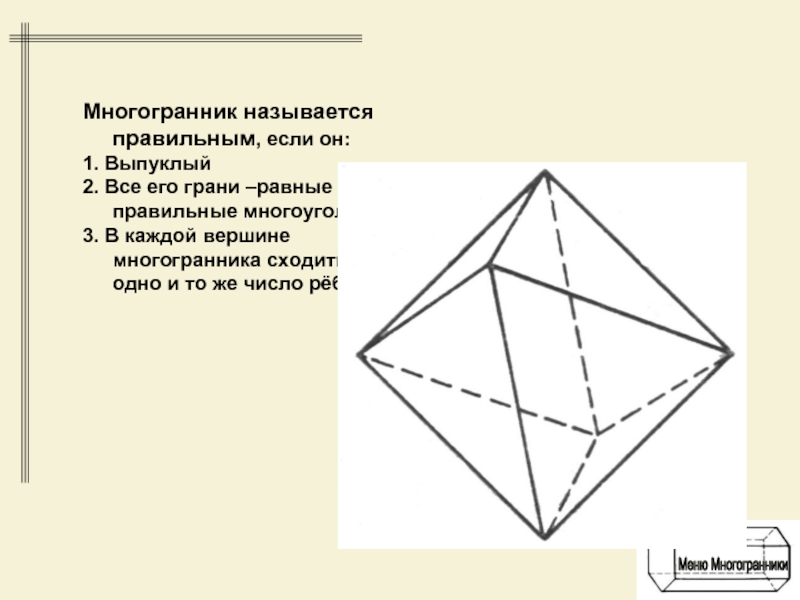
Многогранник называется правильным, если он:
1. Выпуклый
2. Все его грани –равные
правильные многоугольники
3. В каждой вершине многогранника сходиться одно и
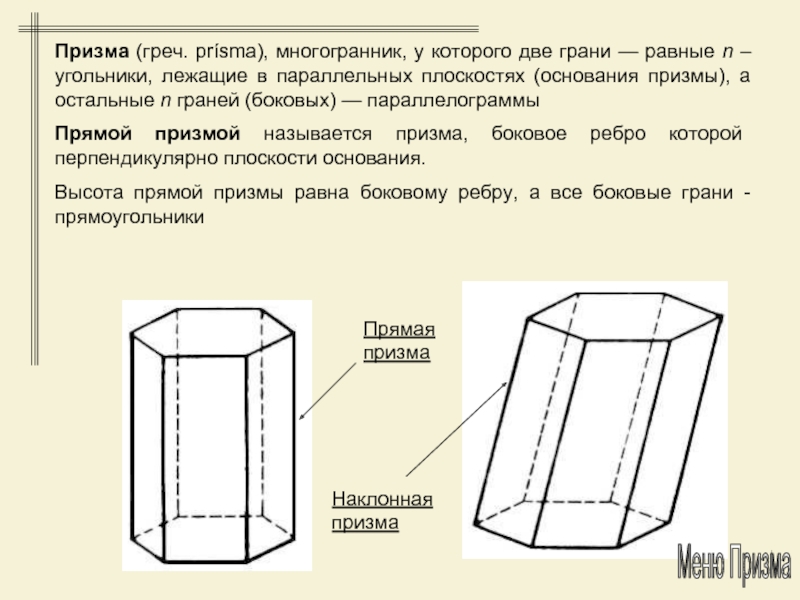
то же число рёберСлайд 10Призма (греч. prísma), многогранник, у которого две грани — равные
n –угольники, лежащие в параллельных плоскостях (основания призмы), а остальные
n граней (боковых) — параллелограммыПрямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания.
Высота прямой призмы равна боковому ребру, а все боковые грани - прямоугольники
Прямая призма
Меню Призма
Наклонная призма
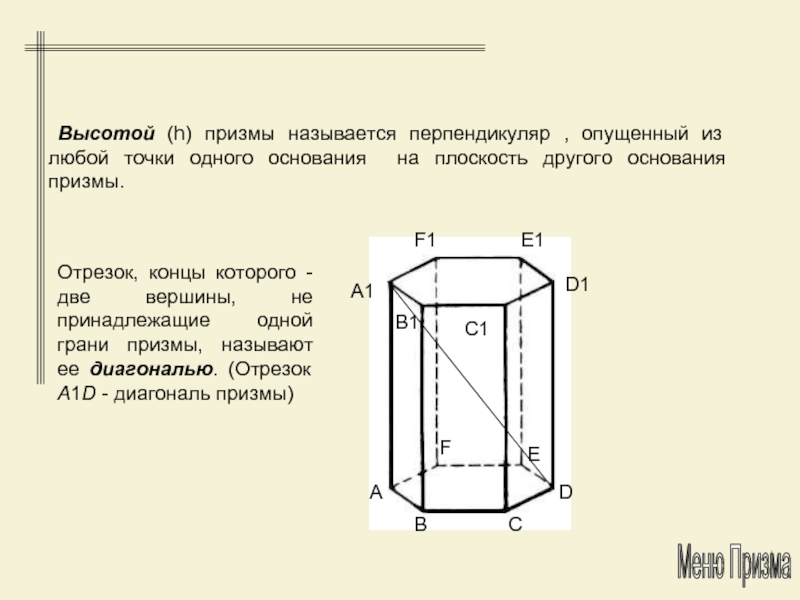
Слайд 12 Высотой (h) призмы называется перпендикуляр , опущенный из любой
точки одного основания на плоскость другого основания призмы.
Отрезок, концы которого
- две вершины, не принадлежащие одной грани призмы, называют ее диагональю. (Отрезок A1D - диагональ призмы)Меню Призма
Слайд 13Правильная призма
Правильной призмой называется прямая призма, основание которой
– правильный многоугольник.
Меню Призма
Слайд 14Нахождение площадей
Площадь поверхности призмы (Sпр) равна сумме площадей
ее боковых граней (площади боковой поверхности Sбок) и площадей двух
оснований (2Sосн) - равных многоугольников: Sпр. =Sбок+2SоснМеню Призма
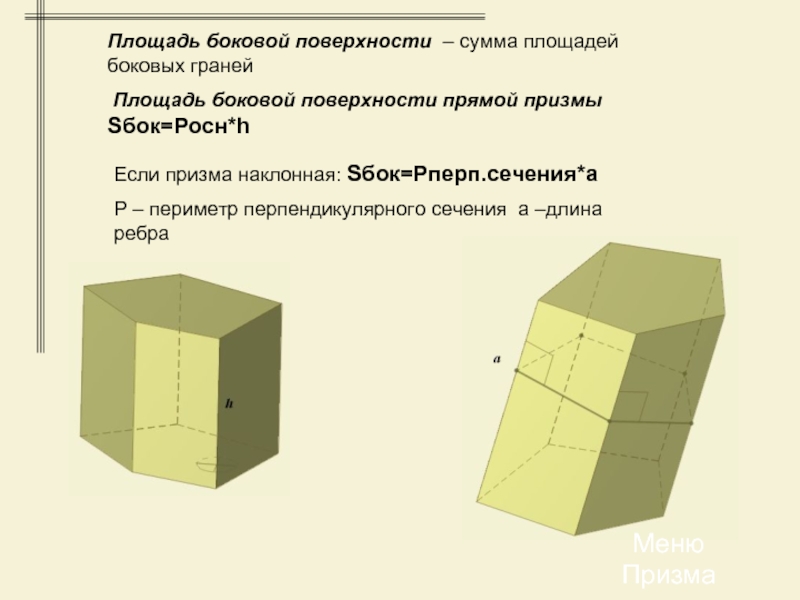
Слайд 15Площадь боковой поверхности – сумма площадей боковых граней
Площадь боковой
поверхности прямой призмы Sбок=Pосн*h
Если призма наклонная: Sбок=Pперп.сечения*a
P – периметр
перпендикулярного сечения a –длина ребра Меню
Призма
Слайд 17 Объём прямой призмы, основанием которой является прямоугольный треугольник, равен
произведению площади основания на высоту.
Меню
Призма
Слайд 18Параллелепипед
Параллелепипедом называется призма, основание которой – параллелограмм.
Прямоугольным параллелепипедом
называется прямой параллелепипед, основание которого – прямоугольник.
Меню Призма
Слайд 19Свойства параллелепипеда
Меню Призма
Противоположные грани параллелепипеда равны параллельны
Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся
этой точкой пополам.Сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его ребер.
Боковые грани прямого параллелепипеда – прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Слайд 21Через одну из сторон основания правильной треугольной призмы проведена плоскость
под углом α к основанию, отсекающая от призмы пирамиду объёма
V. Определить площадь сечения.Задача 1:
Меню Призма
Задачи
Решение
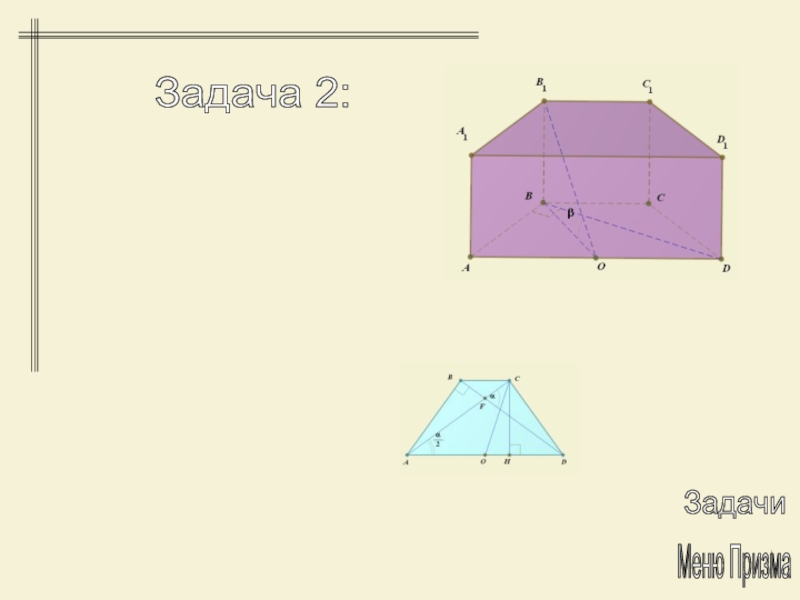
Слайд 23Задача 2:
Меню Призма
Решение
Задачи
В основании прямой призмы –
равнобедренная трапеция, диагонали которой перпендикулярны соответствующим боковым сторонам. Угол между
диагоналями трапеции, противолежащий боковым сторонам, равен α, отрезок, соединяющий вершину верхнего основания с центром окружности, описанной около нижнего основания равен l и образует с плоскостью основания угол β. Найти объём призмы.Слайд 25Меню Призма
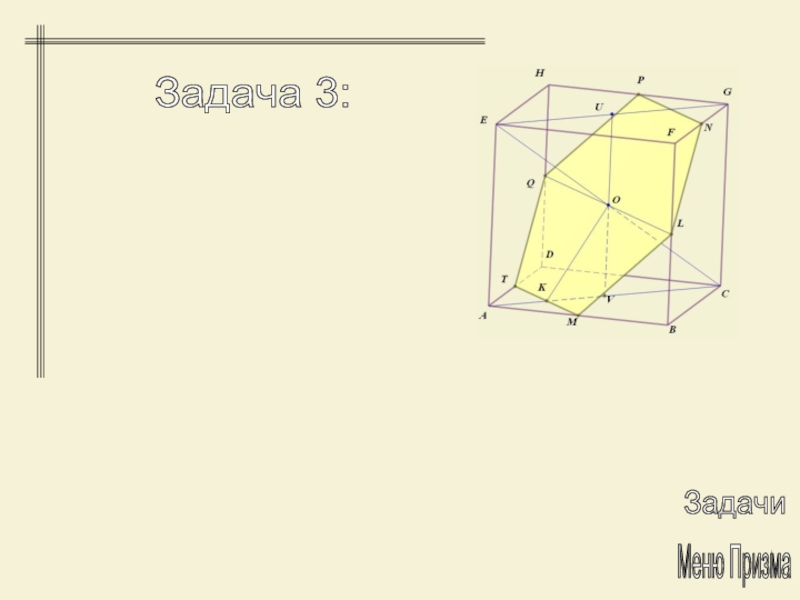
Задача 3:
Решение
Задачи
Через середину диагонали куба, перпендикулярно
к ней проведена плоскость. Определить площадь фигуры, получившейся в сечении
куба этой плоскостью, если ребро куба равно a. EC=CO.Слайд 27Меню Призма
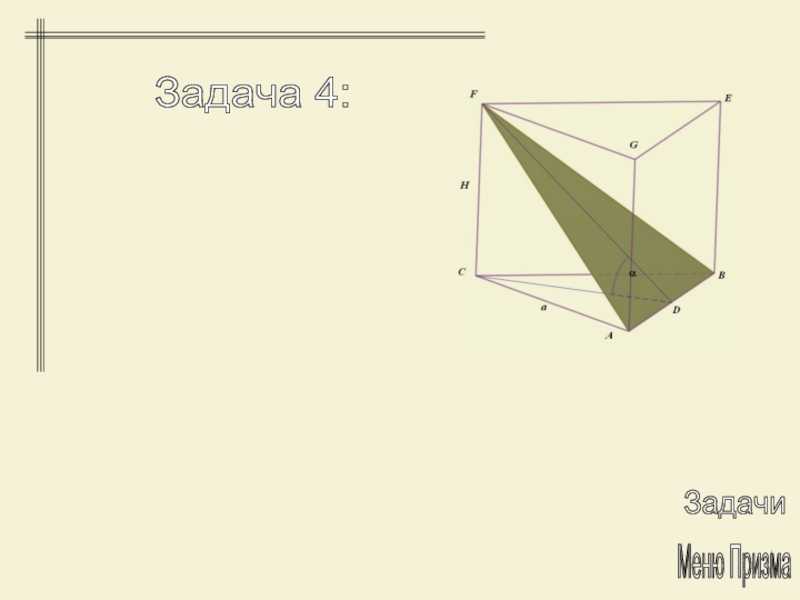
Задача 4:
Решение
Задачи
Дана прямая призма, у которой
основанием служит правильный треугольник. Через одну из сторон нижнего основания
и противоположную вершину верхнего основания проведена плоскость. Угол между этой плоскостью и основанием равен α, а площадь сечения S. Определить V призмы.
Теги