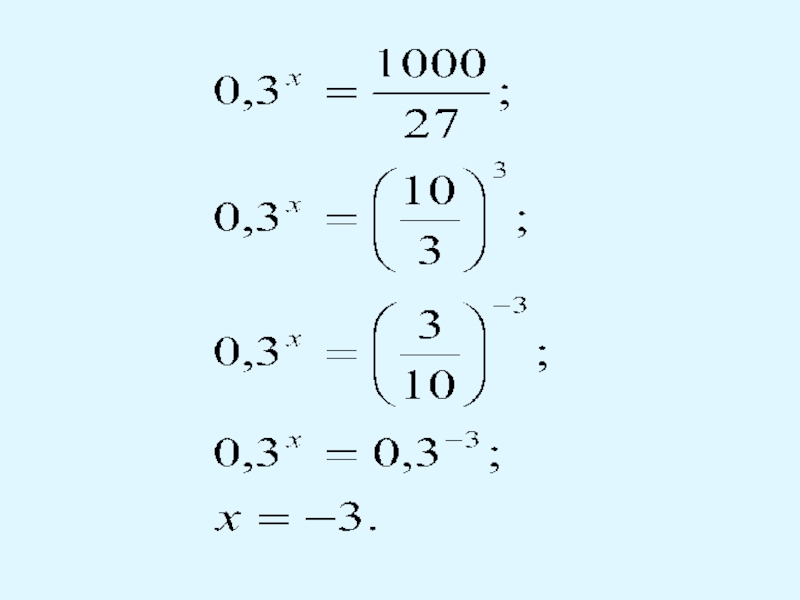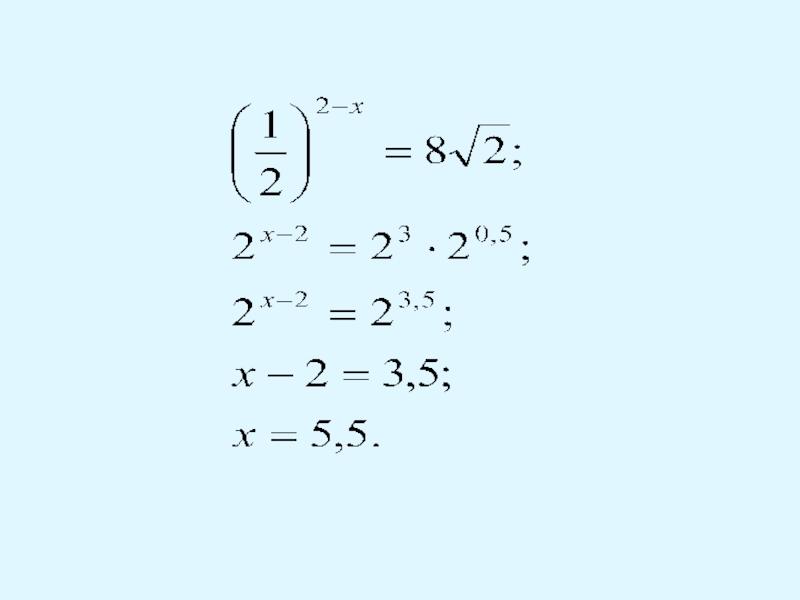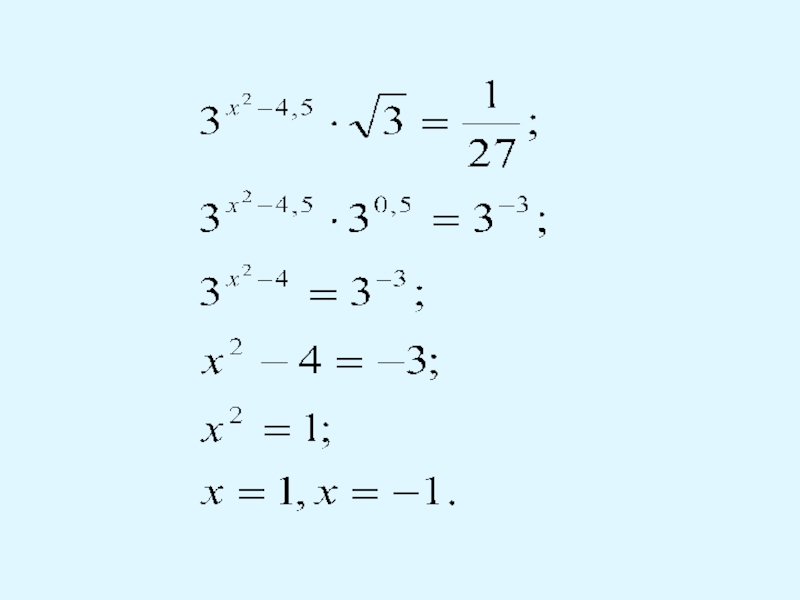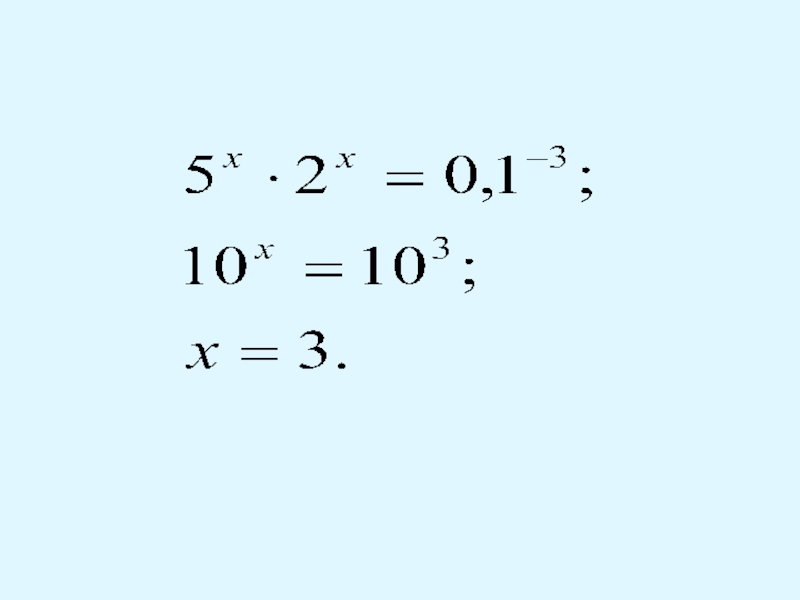Презентация по теме "Методика проведения этапа усвоения при работе с понятиями и умениями с использованием информационных технологий"

с использованием информационных технологий
Выполнила: учитель математики I категории МОУ СОШ

№1 г.Сураж, Белозор Е.В.

изучения новых дидактических единиц (понятий и умений), а именно –

этапа усвоения на примере темы «Показательные уравнения».

Задачи:

1) освоение базовой методики формирования понятий;

2) освоение базовой методики формирования умений;

3) логико-дидактический анализ темы;

4) разработка упражнений, направленных на формирование понятия «показательное уравнение»;

5) разработка упражнений, направленных на формирование умения решать показательные уравнения методом уравнивания показателей степени.

Ю.М.Колягиным, И.Е.Маловой, Н.Л.Стефановой и другими методистами
восприятие и ощущение;
переход от восприятия

к представлению;

переход от представления к понятию;

Психологические ступени формирования понятия, выделенные Ю.М.Колягиным:

образование понятия;

усвоение понятия.

Ю.М.Колягиным, И.Е.Маловой, Н.Л.Стефановой и другими методистами
1) профессиональный (выполнение логико-математического анализа);
2)

подготовительный (актуализация знаний, связь с опытом, мотивация);

3) основной (обучающий);

Н.Л.Стефанова выделила 4 этапа работы с понятием:

4) закрепление (применение при решении типовых задач);

Ю.М.Колягиным, И.Е.Маловой, Н.Л.Стефановой и другими методистами
1) введение определения (конкретно-индуктивным или

абстрактно-дедуктивным методами);

2) усвоение определения (цель: запомнить определение и научиться проверять, подходит объект под рассматриваемое определение или нет);

3) закрепление понятия (итоги: что нового узнали о понятии, что научились делать в связи с рассматривае-мым понятием, какие виды задач научились решать).

И.Е.Малова выделяет 3 этапа методики формирования математических понятий

Ю.М.Колягиным, И.Е.Маловой, Н.Л.Стефановой и другими методистами
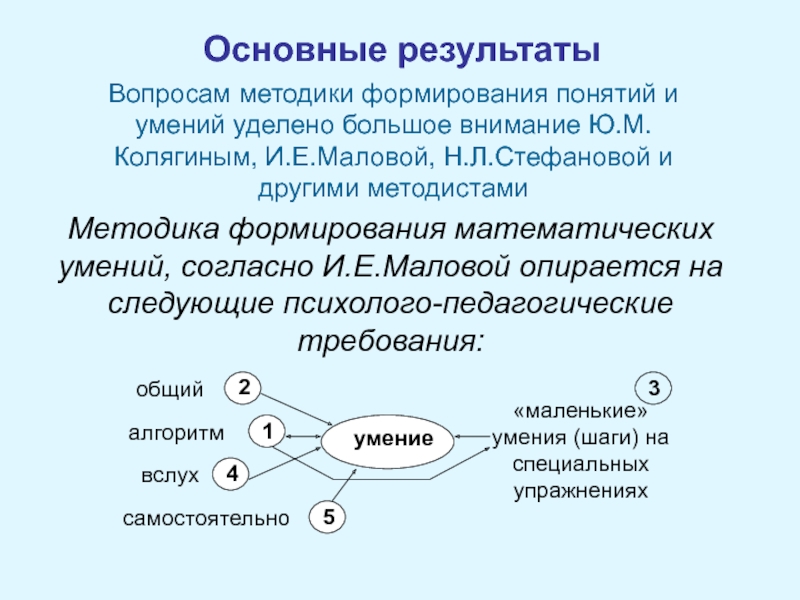
Методика формирования математических умений, согласно

И.Е.Маловой опирается на следующие психолого-педагогические требования:

деятельности обучающихся.
2. Организация индивидуальной поддержки учебной деятельности каждого обучающегося преподавателями.
3.

Организация групповой учебной работы обучающихся.

Наиболее важные проблемы разработки и использования информационно-образовательной среды на основе информационных компьютерных технологий:

на уроках математики показало:
повышение интереса к урокам математики
улучшение дисциплины на

уроках

Информационные технологии обучения - это совокупность методов, форм и средств воздействия на человека в процессе его развития

улучшение успеваемости по другим предметам

повышение внимания и улучшение памяти

сделать вывод: тема «Показательные уравнения» организована дедуктивно-индуктивно, так как дано

определение понятия «показательное уравнение»; опираясь на свойства показательной функции, сформулировано в виде теоремы утверждение, позволяющее при решении показательного уравнения перейти к более простому равносильному уравнению; алгоритмы решения показательных уравнений методом уравнивания показателей, методом введения новой переменной и их систем введены индуктивно на конкретных примерах, анализ решения которых позволяет, сделав обобщение, сформулировать алгоритмы.

Анализ теоретического материала темы.

методом уравнивания показателей;
2) уравнения, решаемые методом замены переменной;
можно выделить следующие

группы упражнений:

Анализ задачного материала темы.

3) уравнения, решаемые функционально-графическим методом;

4) уравнения, решаемые с помощью методов замены переменной и разложения на множители;

5) уравнения с параметром;

6) системы показательных уравнений;

них новые?
_________
________________________
Как их можно назвать?


показательное
показательное
Почему?



Методика формирования понятия «показательное уравнение».

af(x) =

ag(x), (1)
где a – положительное число, отличное от 1,
и уравнения, сводящиеся к этому виду.

Попробуйте иначе сформулировать определение «показательного уравнения».

Какие условия должны обязательно выполняться для показательных уравнений?

______________________________________

Уравнение вида a f(x) = a g(x), где а > 0, a ≠ 1, называется показательным.

Методика формирования понятия «показательное уравнение».

формирования понятия «показательное уравнение».

и

решить его.

1. С помощью равносильных преобразований привести уравнение к виду , где .

.

теорема: Показательное уравнение
где , равносильно уравнению .

Введение алгоритма

Решение:

Алгоритм:

Ответ: 5.

3. Корни уравнения являются корнями исходного показательного уравнения. Записать ответ.

Почему?








+
-
-
-
+
-
+
+

вида? Почему?








НЕТ

вида? Почему?








НЕТ

«СОШ №1 г.Сураж» Брянской области.
Образование: высшее, физико-математический факультет БГПУ им.

И.Г. Петровского.
Стаж работы 10 лет.

внимание!