Многогранные углы

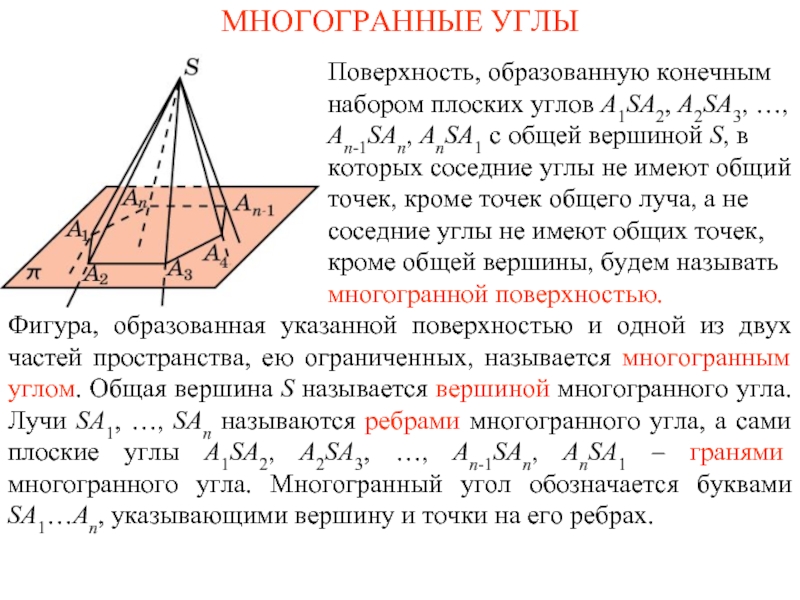
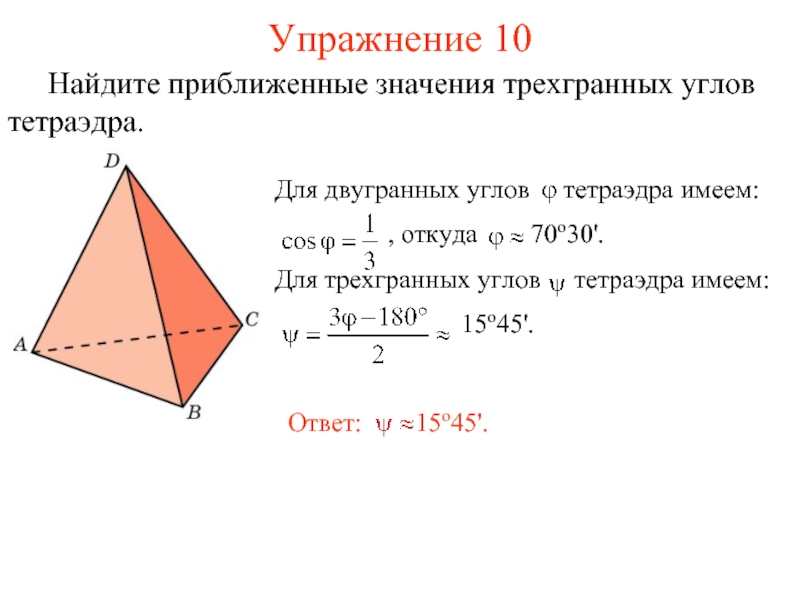
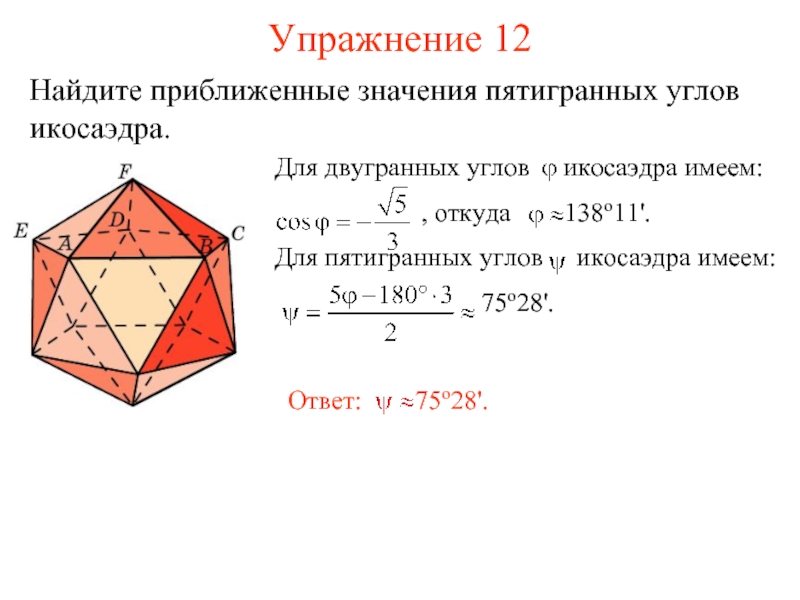
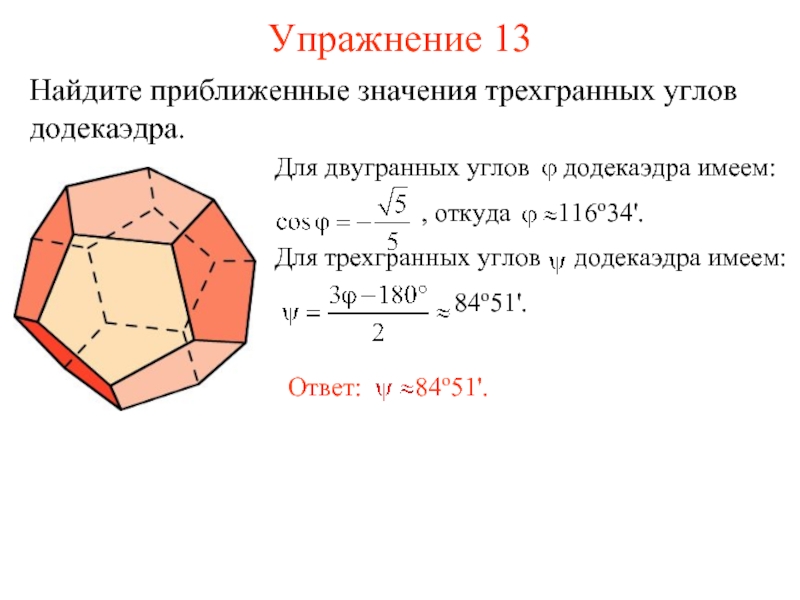
пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется

вершиной многогранного угла. Лучи SA1, …, SAn называются ребрами многогранного угла, а сами плоские углы A1SA2, A2SA3, …, An-1SAn, AnSA1 – гранями многогранного угла. Многогранный угол обозначается буквами SA1…An, указывающими вершину и точки на его ребрах.

Поверхность, образованную конечным набором плоских углов A1SA2, A2SA3, …, An-1SAn, AnSA1 с общей вершиной S, в которых соседние углы не имеют общий точек, кроме точек общего луча, а не соседние углы не имеют общих точек, кроме общей вершины, будем называть многогранной поверхностью.

четырехгранными, пятигранными и т. д.

других его плоских углов.
Доказательство. Рассмотрим трехгранный угол SABC. Пусть наибольший

из его плоских углов есть угол ASC. Тогда выполняются неравенства ∠ASB ≤  ∠ASC <  ∠ASC +  ∠BSC; ∠BSC ≤ ∠ASC <  ∠ASC +  ∠ASB.
Таким образом, остается доказать неравенство ∠ASС <  ∠ASB +  ∠BSC.

Воспользуемся неравенством треугольника AC < AB + BC. Вычитая из обеих его частей AD = AB, получим неравенство DC < BC. В треугольниках DSC и BSC одна сторона общая (SC), SD = SB и DC < BC. В этом случае против большей стороны лежит больший угол и, следовательно,  ∠DSC <  ∠BSC. Прибавляя к обеим частям этого неравенства угол ASD, равный углу ASB, получим требуемое неравенство  ∠ASС <  ∠ASB +  ∠BSC.

Отложим на грани ASC угол ASD, равный ASB, и точку B выберем так, чтобы SB = SD. Тогда треугольники ASB и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB = AD.

трехгранных углов с вершинами B и С имеют место неравенства: 

∠ ABС <  ∠ ABS +  ∠ CBS,  ∠ ACB <  ∠ ACS +  ∠BCS. Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем 180°<  ∠ BAS + ∠ CAS +  ∠ ABS +  ∠ CBS + ∠ BCS +  ∠ ACS = 180° -  ∠ ASB + 180° -  ∠ BSC + 180° -  ∠ ASC. Следовательно,  ∠ ASB +  ∠ BSC +  ∠ ASC < 360° .

Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу доказанного свойства, имеет место неравенство  ∠ BAС <  ∠BAS +  ∠ CAS.

фигурой, т. е. вместе с любыми двумя своими точками целиком

содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов.

Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°.

Доказательство аналогично доказательству соответствующего свойства для трехгранного угла.

вертикальных углов
Теорема. Вертикальные углы равны.

величиной соответствующего линейного угла и равна 180о, то будем считать,

что градусная величина всего пространства, которое состоит из двух развернутых двугранных углов, равна 360о. Величина многогранного угла, выраженная в градусах, показывает какую часть пространства занимает данный многогранный угол. Например, трехгранный угол куба занимает одну восьмую часть пространства и, значит, его градусная величина равна 360о:8 = 45о. Трехгранный угол в правильной n-угольной призме равен половине двугранного угла при боковом ребре. Учитывая, что этот двугранный угол равен , получаем, что трехгранный угол призмы равен  .

двугранные углы. Опишем около вершины S трехгранного угла единичную сферу

и обозначим точки пересечения ребер трехгранного угла с этой сферой A, B, C.
Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360о плюс учетверенная величина трехгранного угла, или
∠ SA + ∠ SB +  ∠ SC = 180о + 2 ∠ SABC.

на трехгранные углы, проведением диагоналей A1A3, …, A1An-1 и применяя

к ним полученную формулу, будем иметь:
∠ SA1 + … + ∠ SAn = 180о(n – 2) + 2 ∠ SA1…An.

Многогранные углы можно измерять и числами. Действительно, тремстам шестидесяти градусам всего пространства соответствует число 2π. Переходя от градусов к числам в полученной формуле, будем иметь:
∠SA1+ …+∠SAn = π (n – 2) + 2∠SA1…An.

30°, 60°, 20°; б) 45°, 45°, 90°; в) 30°, 45°,

60°?

Ответ: а) Нет;

б) нет;

в) да.

образуют только: а) трехгранные углы; б) четырехгранные углы; в) пятигранные

углы.

Ответ: а) Тетраэдр, куб, додекаэдр;

б) октаэдр;

в) икосаэдр.

В каких границах находится третий плоский угол?
Ответ: 10о < ϕ

< 150о.

Найдите величину угла между плоскостями плоских углов в 45°.
Ответ:

90о.

двугранный угол между ними прямой. Найдите третий плоский угол.
Ответ: 60о.

На его ребрах от вершины отложены равные отрезки OA, OB,

OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC.

Ответ: 90о.

из его ребер отложен от вершины отрезок, равный 3 см,

и из его конца опущен перпендикуляр на противоположную грань. Найдите длину этого перпендикуляра.

его граней.
Ответ: Луч, вершиной которого является вершина трехгранного угла, лежащий

на линии пересечения плоскостей, делящих двугранные углы пополам.

его ребер.
Ответ: Луч, вершиной которого является вершина трехгранного угла, лежащий

на линии пересечения плоскостей, проходящих через биссектрисы плоских углов и перпендикулярных плоскостям этих углов.

см, высота 1 см. Найдите четырехгранный угол при вершине этой

пирамиды.

при вершине 90о. Найдите трехгранный угол при вершине этой пирамиды.

высота Найдите трехгранный угол при вершине этой пирамиды.