Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неравенства
Содержание
- 1. Неравенства
- 2. СодержаниеНеравенства с одной переменнойЛинейные неравенстваКвадратные неравенстваРациональные неравенстваНеравенства, содержащие знак модуляКомбинированные неравенства
- 3. Неравенства вида Где
- 4. Линейным неравенством называется неравенство вида
- 5. A1. Укажите наименьшее целое решение неравенстваРешение.Ответ: -
- 6. Квадратными неравенствами называются неравенства вида
- 7. А1. Решите неравенство Решение.D = 49; Построим эскиз графика функции Из графика следует, что y
- 8. А2. Решите неравенствоРешение.D < 0 =>
- 9. Рациональным неравенством называется неравенство вида
- 10. При решении рациональных неравенств методом интервалов нужно:все
- 11. A1. Найдите наименьшее целое решение неравенства-437x-+-+//////////////////////////////////////////////1) -52) -43) -34) -1Решение.Ответ: -4
- 12. А2. Укажите число целых решений неравенства
- 13. В1. Найдите сумму целых решений неравенстваРешение.-33-+-+/////////////////////////////////1+-3 +
- 14. В2. Укажите сумму целых чисел, не являющихся
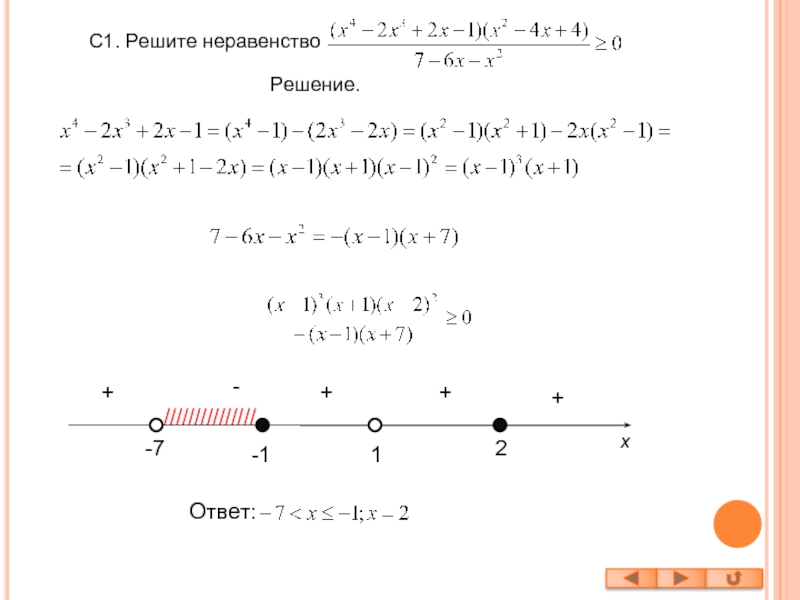
- 15. С1. Решите неравенствоРешение.-72++-+///////////////1+x-1Ответ:
- 16. С2. Решите неравенствоРешение.Преобразуем левую часть неравенства, приведя дроби к общему знаменателю:-25++-+/////////////-1-x-1,251-///////////////////////////Ответ:
- 17. С3. Решите неравенствоРешение.Пусть , тогда -15+-+////////////////////////////////////////////////////////////////tили1)-2-1+-+x//////////2)-41+-+x//////////илиОтвет://////////
- 18. С4. Решите неравенствоРешение.Пусть, тогда+-+////////////////////////////////////////////t--3,25-12t < -3,5 или -1 < t < 2
- 19. 1) 2)решений нет;Ответ: ( - 2; 1)
- 20. Неравенства, содержащие знак модуляеслиеслигде
- 21. А1. Найдите число целых решений неравенстваРешение.0; 1;
- 22. А2. Решите неравенствоРешение.Так как
- 23. А3. Решите неравенство1)Решений нет3)(-1;1)Решение.Так как
- 24. С1. Решите неравенствоРешение.-52+-+x//////////////////////-14+-+x//////////////////////Ответ:или
- 25. C2. Решите неравенство Решение.Так какдля всех x, то13+-+x//////////1
- 26. С3. Решите неравенствоРешение.+---++-22X + 2X - 2Решим
- 27. 3)Ответ:
- 28. С4. Решите неравенствоРешение.Построим графики функцийиy = f
- 29. B1.Найдите количество целочисленных решений неравенстваРешение.Так как
- 30. В2.Найти количество целочисленных решений неравенстваРешение.15x-++////////////////////1; 2; 3;
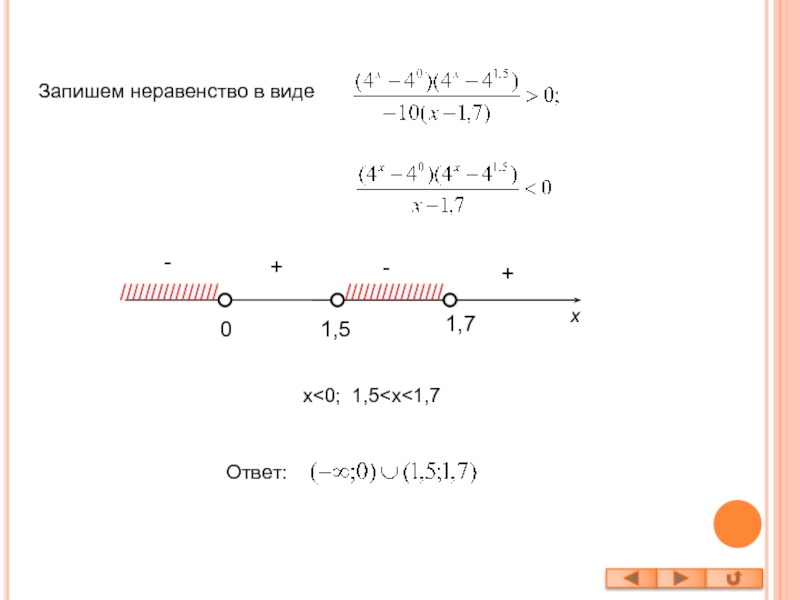
- 31. С1.Найдите все значения x, для которых точки
- 32. 1,7--+////////////////+x////////////////1,50Ответ:Запишем неравенство в видеx
- 33. С2. Решите неравенствоРешение.ОДЗ: x > 0;пустьтогда
- 34. ЛитератураЕГЭ 2009. Математика: сборник заданий/ В.В. Кочагин,
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Содержание
Неравенства с одной переменной
Линейные неравенства
Квадратные неравенства
Рациональные неравенства
Неравенства, содержащие знак модуля
Комбинированные
неравенства
Слайд 3Неравенства вида
Где и
- линейные функции, называются неравенствами с одной неизвестной.
Решением
неравенства с одной переменной называется такое значение переменной, при подстановке которого неравенство обращается в верное числовое неравенство.Решить неравенство – значит найти все его решения или доказать, что решений нет.
Слайд 4Линейным неравенством называется неравенство вида
(или
)Решая линейное неравенство вида , получим:
1 случай: тогда
2 случай: тогда
3 случай: , тогда
Если при этом то решений нет
Если , то
Слайд 5
A1. Укажите наименьшее целое решение неравенства
Решение.
Ответ: - 3
1) – 5;
2) – 4; 3) – 3; 4) – 2;
Слайд 6Квадратными неравенствами называются неравенства вида
где x – переменная; a,b,c – действительные числа, причем a 0.
Способы решения
графический
аналитический
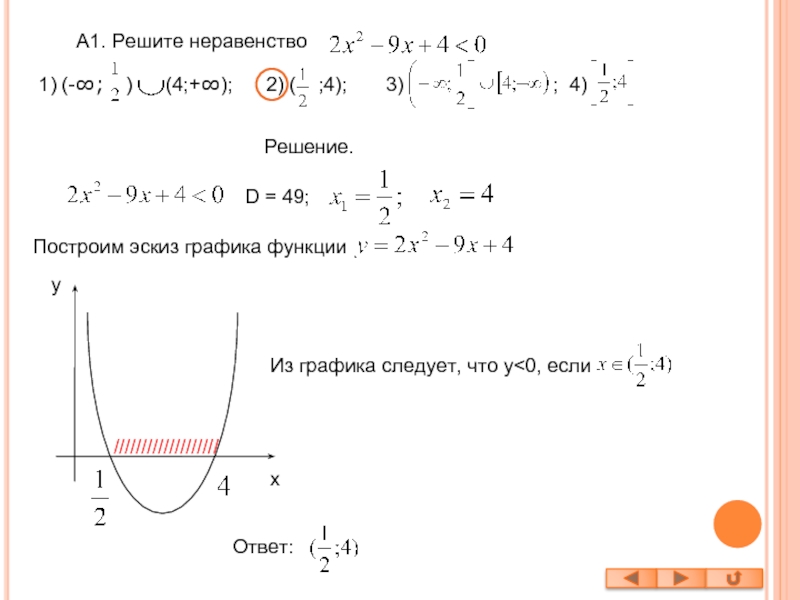
Слайд 7А1. Решите неравенство
Решение.
D = 49;
Построим эскиз графика функции
Из графика следует, что y
) (4;+∞); 2) ( ;4); 3) ; 4) x
y
Слайд 8А2. Решите неравенство
Решение.
D < 0 => график функции
с
осью абсцисс не
пересекается
Из графика следует, что y
1) (-∞;+∞); 2) – 0,5; 3) решений нет; 4) 5;
x
y
Слайд 9Рациональным неравенством называется неравенство вида
,
,
, ,где , - многочлены
Основной метод решения – метод интервалов
Слайд 10При решении рациональных неравенств методом интервалов нужно:
все члены неравенства перенести
в левую часть; если неравенство дробно – рациональное, то привести
левую часть к общему знаменателю;найти все значения переменной, при которых числитель и знаменатель обращаются в 0;
нанести найденные точки на числовую прямую, разбивая ее при этом на интервалы, в каждом из которых рациональная функция сохраняет знак;
определить знак функции на любом из интервалов (лучше крайнем);
определить знаки на остальных интервалах: при переходе через точу знак меняется на противоположный, если точка является корнем нечетной степени кратности; при переходе через точку четной кратности знак сохраняется;
множеством решений неравенства является объединение интервалов с соответствующим знаком функции. В случае нестрогого неравенства к этому множеству добавляются корни числителя.
Слайд 11A1. Найдите наименьшее целое решение неравенства
-4
3
7
x
-
+
-
+
/////////////////////////
/////////////////////
1) -5
2) -4
3) -3
4) -1
Решение.
Ответ:
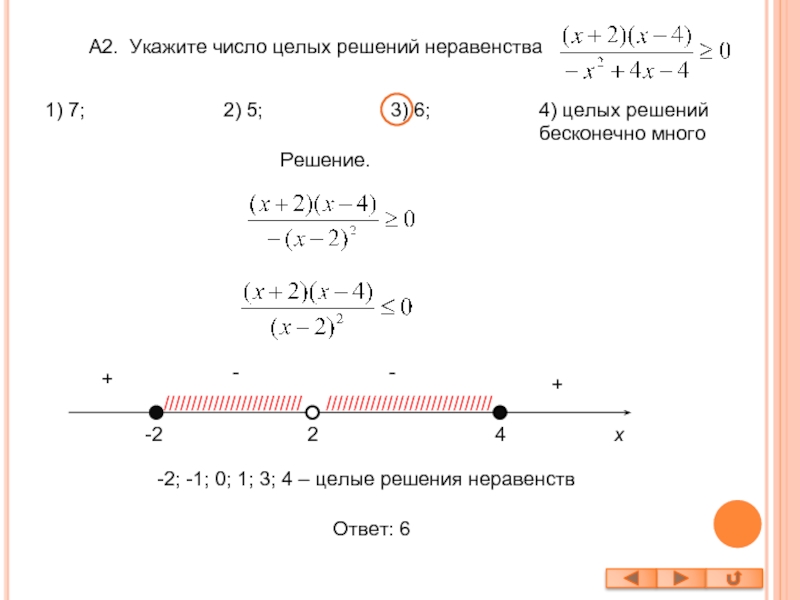
Слайд 12А2. Укажите число целых решений неравенства
Решение.
-2
2
4
-
+
-
+
/////////////////////////
//////////////////////////////
-2; -1;
0; 1; 3; 4 – целые решения неравенств
Ответ: 6
x
1) 7;
2) 5; 3) 6; 4) целых решений бесконечно много
Слайд 13В1. Найдите сумму целых решений неравенства
Решение.
-3
3
-
+
-
+
/////////////////
////////////////
1
+
-3 + (-2) + (-1)
+ 2 + 3 = -1
Ответ: -1
x
3; -2; -1;
2; 3 – целые решения неравенства.Слайд 14В2. Укажите сумму целых чисел, не являющихся решением неравенства
Решение.
-1
1
-
+
-
+
////////////
////////////////
+
x
//////////////////
-1; 0;
1 – целые числа, не являющиеся решениями неравенства
-1+ 0 +
1 = 0Ответ: 0
Слайд 16С2. Решите неравенство
Решение.
Преобразуем левую часть неравенства, приведя дроби к общему
знаменателю:
-2
5
+
+
-
+
/////////////
-1
-
x
-1,25
1
-
////////////
///////////////
Ответ:
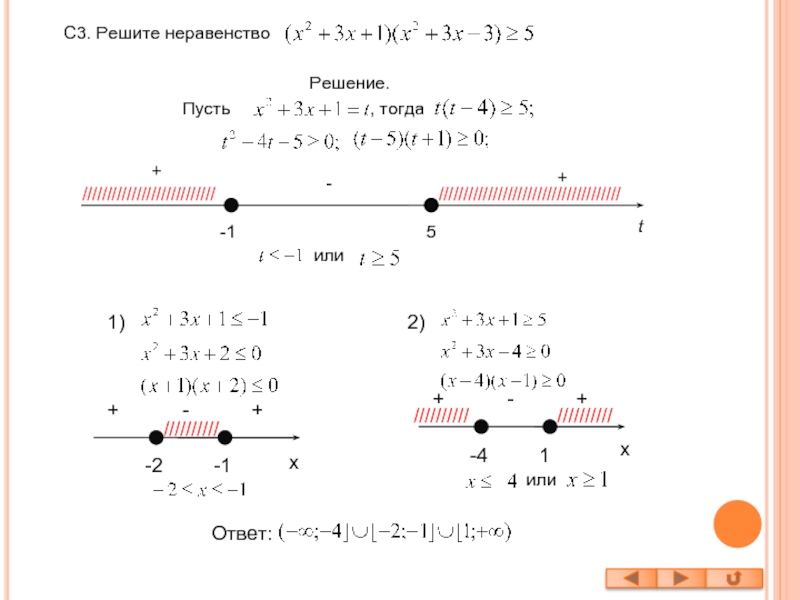
Слайд 17С3. Решите неравенство
Решение.
Пусть
, тогда
-1
5
+
-
+
///////////////////////////
/////////////////////////////////////
t
или
1)
-2
-1
+
-
+
x
//////////
2)
-4
1
+
-
+
x
//////////
или
Ответ:
//////////
Слайд 18С4. Решите неравенство
Решение.
Пусть
, тогда
+
-
+
/////////////////////
///////////////////////
t
-
-3,25
-1
2
t < -3,5 или
-1 < t < 2
Слайд 21А1. Найдите число целых решений неравенства
Решение.
0; 1; 2; 3 –
целые решения неравенства
Ответ: 4
1) 3;
2) 4; 3) 5; 4) целых решений бесконечно много.
Слайд 22А2. Решите неравенство
Решение.
Так как
, то исходное неравенство решений
не имеетОтвет: решений нет
4) решений нет
Слайд 23А3. Решите неравенство
1)Решений нет
3)(-1;1)
Решение.
Так как
,
то исходное неравенство справедливодля любого действительного x
Ответ: (-∞;+∞)
Слайд 24С1. Решите неравенство
Решение.
-5
2
+
-
+
x
/////////
/////////////
-1
4
+
-
+
x
/////////////////
/////
Ответ:
или
Слайд 26С3. Решите неравенство
Решение.
+
-
-
-
+
+
-2
2
X + 2
X - 2
Решим неравенство в каждом
из трех промежутков
1)
2)
Используем метод интервалов для модулей
Слайд 28С4. Решите неравенство
Решение.
Построим графики функций
и
y = f (x)
y = f
(x)
y
x
2
1
6
График функции f(x) расположен ниже графика функции g(x) при
Ответ:
( 0; 6)0
9
Найдем абсциссы точек пересечения графиков
Слайд 29B1.
Найдите количество целочисленных решений неравенства
Решение.
Так как
при
, то-2
5
+
-
+
x
//////////
- 2; -1; 0; 1; 2 - целые решения неравенства
Ответ: 5
Слайд 30В2.Найти количество целочисленных решений неравенства
Решение.
1
5
x
-
+
+
////////////////////
1; 2; 3; 4; 5 –
целые решения неравенства
Условию
удовлетворяют числа 2 и 4
Ответ: 2
Слайд 31С1.Найдите все значения x, для которых точки графика функции
лежат
выше соответствующих точек графика функции
Составим неравенство, которому удовлетворяют значения
x: Найдем те точки, в которых обращаются в ноль числитель и знаменатель дроби:
б)
а)
Решим данное неравенство методом интервалов
Решение.
Слайд 34Литература
ЕГЭ 2009. Математика: сборник заданий/ В.В. Кочагин, М.Н. Кочагина. –
М.: Эксмо, 2008
ЕГЭ 1009. Математика: сборник экзаменационных заданий / Авт.-
сост. Л.О. Денищева и др. – М.: Эксмо, 2009Математика. Подготовка К ЕГЭ / Г.Г. Мамонтова. – М.: Новое знание, 2008
ЕГЭ 2009, Математика. Справочник / Авт. – сост. А.М. Титаренко и др. – М.: Эксмо, 2008
Математика: практикум для старшеклассников и абитуриентов / Авт. – сост. А.В. Борзенков. – Волгоград: Учитель, 2009
ЕГЭ. Математика: Раздаточный материал тренировочных тестов / С.Л. Никушкина, О.И. Судавная. – СПб.: Тригон, 2009
Система подготовки к ЕГЭ по математике. А.Семенов, Е.Юрченко. – Газета «Математика» №21, 2008