TheSlide.ru

Обратные тригонометрические функции

Содержание

1. Обратные тригонометрические функции
2. sint = 0,5sint = 0,3При каких значениях t верно равенство?, t=?
3. Область определения функции — множество R всех
4. Область определения функции — множество R всех
5. Определениеarcsin t = aarcsin(-x) = - arcsinx
6. Обратные тригонометрические функцииОпределение Арксинусом числа
7. у = arcsinxх1)Область определения: отрезок [-1; 1];
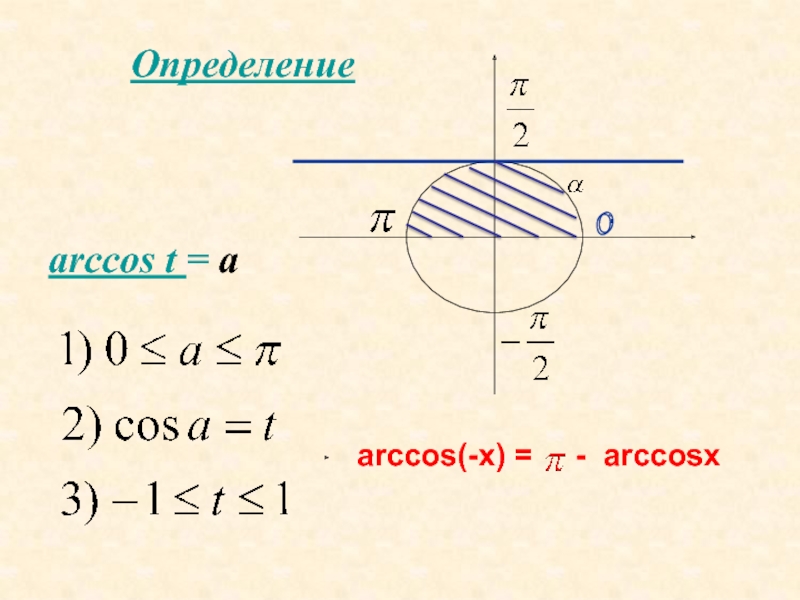
8. Определениеarccos t = aarccos(-x) = - arccosx
9. Определение Аркосинусом числа
10. у=arccos x1)Область определения: отрезок [-1; 1]; 2)Область
11. Слайд 11
12. Определениеarctg t = a
13. Обратные тригонометрические функцииОпределение Арктангенсом числа
14. Функция у = arctg xD
15. Определениеarcctg t = a
16. Обратные тригонометрические функцииОпределениеАрккосинусом числа
17. Функция у = arсctg xD (f) =
18. Функция y = arctgxФункция y = arcctgx
19. Работаем устноarcsin(-x) = - arcsinxarccos(-x) = - arccosx
20. Работаем устноИмеет ли смысл выражение?
21. Упражнение 3Имеет ли смысл выражение:arcsin(-1/2)
22. Работаем устноНайдите значения выражений:
23. Работаем устноarctg(-x) = - arctgxarcctg(-x) = - arcctgx
24. Упражнение а) б)
25. Свойства аркфункций
26. Тригонометрические операции над обратными тригонометрическими функциями
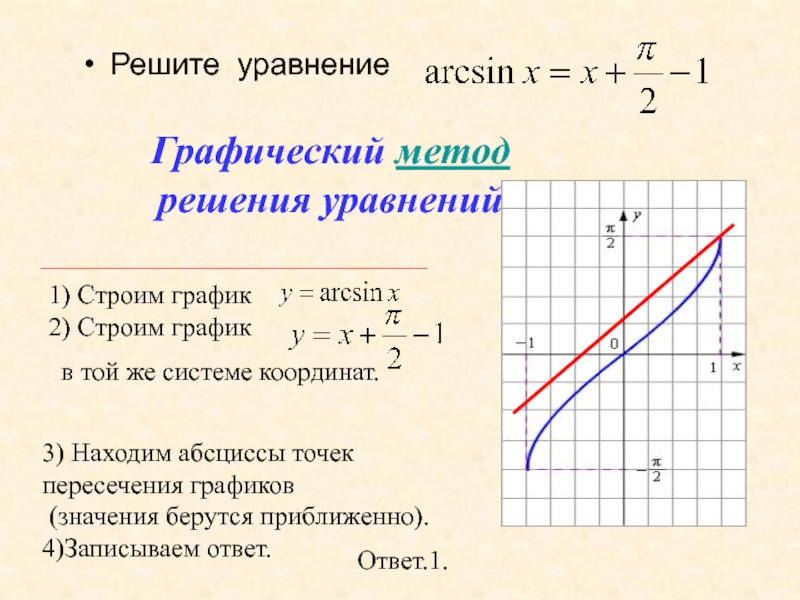
27. Решите уравнение Ответ.1.3) Находим абсциссы точек пересечения графиков (значения берутся приближенно).4)Записываем ответ.Графический метод решения уравнений
28. Функционально-графическийметод решения уравненийПример: решите равнение3) Уравнение f(x)=g(x)
29. Обратные тригонометрические функции
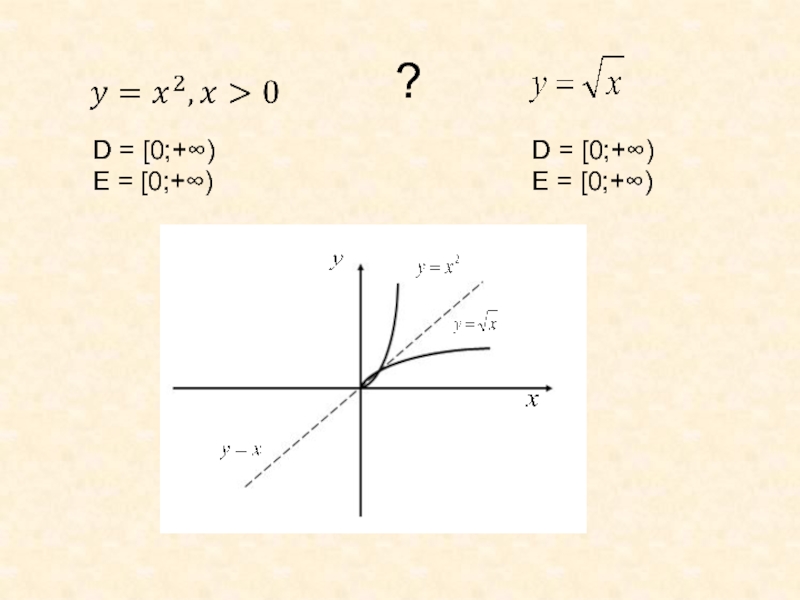
30. D = [0;+∞)E = [0;+∞) D = [0;+∞)E = [0;+∞) ?
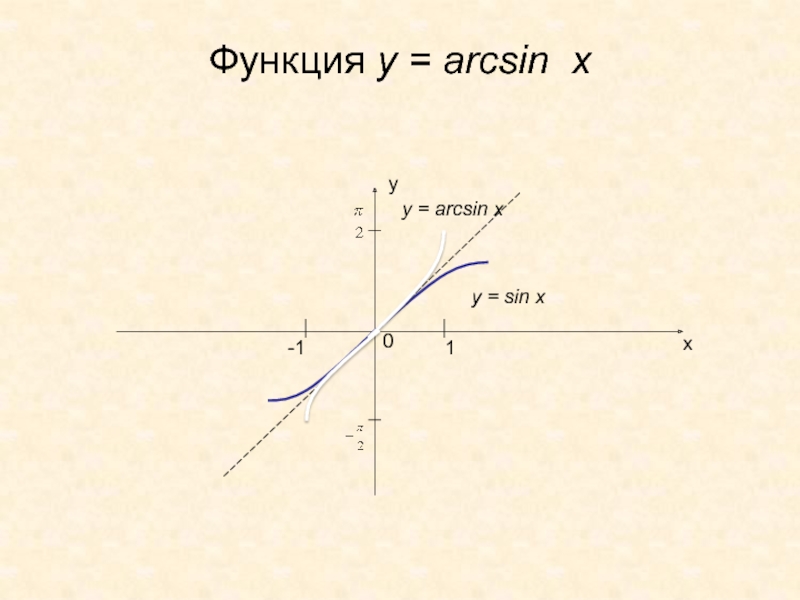
31. Функция y = arcsin xух0-11y = sin xy = arcsin x
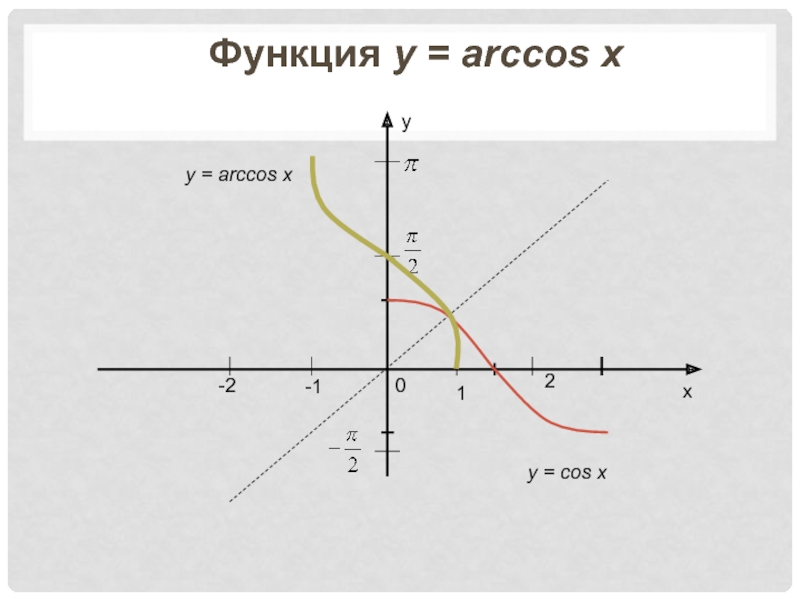
32. ху12-1-20Функция у = arccos xy = arccos xy = cos x
33. Скачать презентанцию

sint = 0,5sint = 0,3При каких значениях t верно равенство?, t=?

Главная
Математика
Обратные тригонометрические функции

Слайды и текст этой презентации

Слайд 1

Обратные
тригонометрические
функции

Обратныетригонометрические функции

Слайд 2
sint = 0,5
sint = 0,3
При каких

значениях t верно равенство?
,
t=?

sint = 0,5sint = 0,3При каких значениях t верно равенство?, t=?

Слайд 3Область определения функции — множество R всех действительных чисел.

Множество значений

функции — отрезок [-1; 1], т.е. синус функция — ограниченная.

Функция

нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.

Функция периодическая с наименьшим положительным периодом 2π:

Функция у = sinx

Область определения функции — множество R всех действительных чисел.Множество значений функции — отрезок [-1; 1], т.е. синус

Слайд 4Область определения функции — множество R всех действительных чисел.

Множество значений

функции — отрезок [-1; 1], т.е. косинус функция — ограниченная.

Функция

четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.

Функция периодическая с наименьшим положительным периодом 2π:

Функция у = cosx

Область определения функции — множество R всех действительных чисел.Множество значений функции — отрезок [-1; 1], т.е. косинус

Слайд 5Определение
arcsin t = a
arcsin(-x) = - arcsinx

Определениеarcsin t = aarcsin(-x) = - arcsinx

Слайд 6Обратные тригонометрические функции
Определение
Арксинусом числа

называется угол (число) из промежутка

синус которого равен

Примеры:

Функция y = arcsinx - нечетная, т.к. arcsin(-x) = - arcsinx

Обратные тригонометрические функцииОпределение Арксинусом числа называется угол (число) из промежутка

Слайд 7у = arcsinx
х
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок

;
3)Функция у = arcsin x нечетная:
arcsin (-x) =

- arcsin x;

4)Функция у = arcsin x монотонно возрастающая;

у = arcsinxх1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция у = arcsin x нечетная:

Слайд 8Определение
arccos t = a
arccos(-x) = - arccosx

Определениеarccos t = aarccos(-x) = - arccosx

Слайд 9Определение
Аркосинусом числа называется

угол (число) из промежутка
косинус которого равен
Обратные тригонометрические функции
Примеры
Функция

y = arccosx - общего вида, т.к. arccos(-x) = π - arccosx

Определение Аркосинусом числа называется угол (число) из промежуткакосинус которого равен

Слайд 10у=arccos x
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция

у = arcсos x четная:
arcscos (-x) =
4)Функция у

= arcсosx монотонно убывающая;

у=arccos x1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у = arcсos x четная: arcscos (-x)

Слайд 11

Слайд 12Определение
arctg t = a

Определениеarctg t = a

Слайд 13Обратные тригонометрические функции
Определение
Арктангенсом числа

называется угол (число) из промежутка

тангенс которого равен

Примеры:

Функция y = arctgx - нечетная, т.к. arctg(-x) = - arctgx

Обратные тригонометрические функцииОпределение Арктангенсом числа называется угол (число) из

Слайд 14
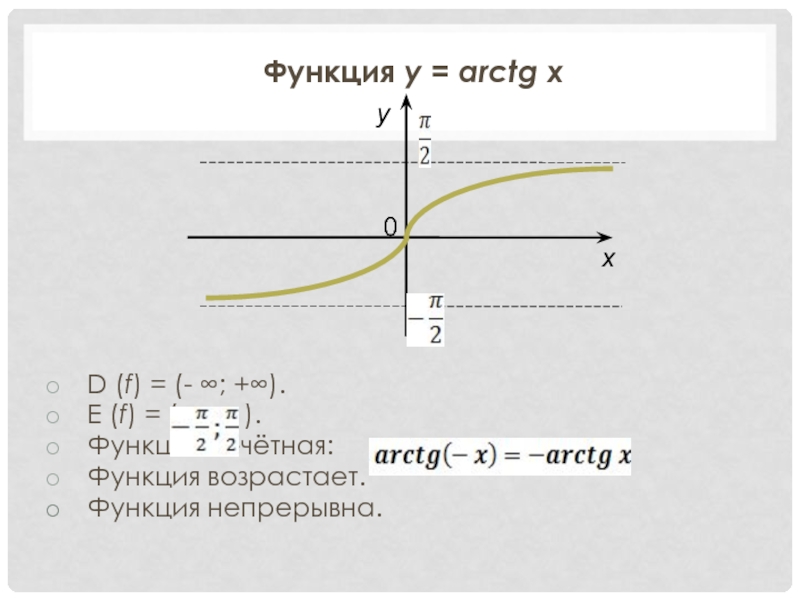
Функция у = arctg x

D (f) = (-

∞; +∞).
E (f) = (

).
Функция нечётная:
Функция возрастает.
Функция непрерывна.

x

0

y

Функция у = arctg xD (f) = (- ∞; +∞). E (f) = (

Слайд 15Определение
arcctg t = a

Определениеarcctg t = a

Слайд 16Обратные тригонометрические функции
Определение
Арккосинусом числа

называется угол (число) из промежутка
котангенс которого равен

Примеры:

Функция y = arctgx - нечетная, т.к. arctg(-x) = - arctgx

Обратные тригонометрические функцииОпределениеАрккосинусом числа называется угол (число) из промежутка

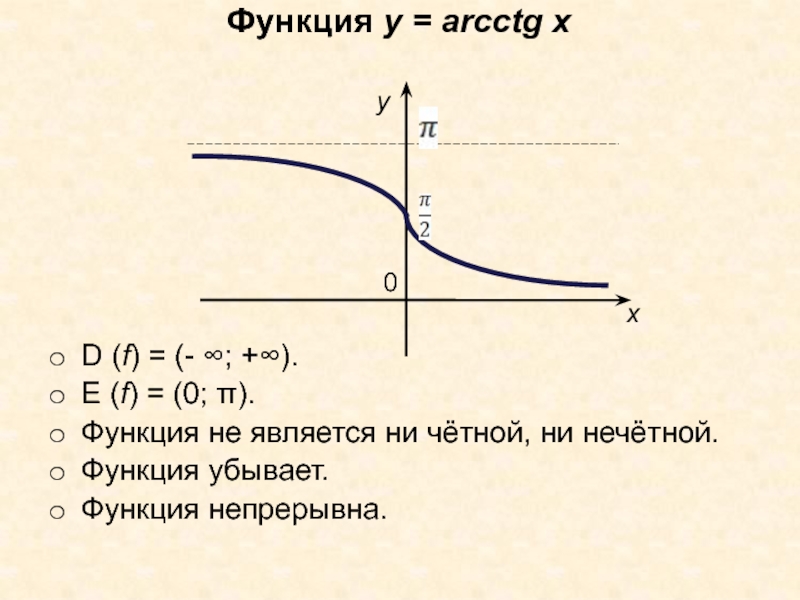
Слайд 17Функция у = arсctg x

D (f) = (- ∞; +∞).
E

(f) = (0; π).
Функция не является ни чётной, ни нечётной.
Функция

убывает.
Функция непрерывна.

y

x

0

Функция у = arсctg xD (f) = (- ∞; +∞).E (f) = (0; π).Функция не является ни

Слайд 18Функция y = arctgx
Функция y = arcctgx

Функция y = arctgxФункция y = arcctgx

Слайд 19Работаем устно
arcsin(-x) = - arcsinx
arccos(-x) = - arccosx

Работаем устноarcsin(-x) = - arcsinxarccos(-x) = - arccosx

Слайд 20Работаем устно
Имеет ли смысл выражение?

Работаем устноИмеет ли смысл выражение?

Слайд 21Упражнение 3
Имеет ли смысл выражение:

arcsin(-1/2)

arccos arcsin(3 -

)
да нет нет

arcsin1,5 arccos(- +1 ) arccos
нет да да

Упражнение 3Имеет ли смысл выражение:arcsin(-1/2) arccos

Слайд 22Работаем устно
Найдите значения выражений:

Работаем устноНайдите значения выражений:

Слайд 23Работаем устно
arctg(-x) = - arctgx
arcctg(-x) = - arcctgx

Работаем устноarctg(-x) = - arctgxarcctg(-x) = - arcctgx

Слайд 24Упражнение
а) б)

в) г)

а)

б) в) г)

а) б) в) г)

а) б) в) г)

а) б) в) г)

а) б) в) г)

Упражнение а) б) в) г)

Слайд 25Свойства аркфункций

Свойства аркфункций

Слайд 26Тригонометрические операции над обратными тригонометрическими функциями

Тригонометрические операции над обратными тригонометрическими функциями

Слайд 27Решите уравнение
Ответ.1.
3) Находим абсциссы точек
пересечения графиков
(значения берутся

приближенно).
4)Записываем ответ.
Графический метод решения уравнений

Решите уравнение Ответ.1.3) Находим абсциссы точек пересечения графиков (значения берутся приближенно).4)Записываем ответ.Графический метод решения уравнений

Слайд 28Функционально-графический
метод решения уравнений
Пример: решите равнение
3) Уравнение f(x)=g(x) имеет не более

одного корня.
4) Подбором находим, что x=0.
Ответ. 0.
Решение.
1) у =arccosx убывает

на области определения

Функционально-графическийметод решения уравненийПример: решите равнение3) Уравнение f(x)=g(x) имеет не более одного корня.4) Подбором находим, что x=0.Ответ. 0.Решение.1)

Слайд 29Обратные тригонометрические функции

Обратные тригонометрические функции

Слайд 30D = [0;+∞)
E = [0;+∞)
D = [0;+∞)
E = [0;+∞)

?

D = [0;+∞)E = [0;+∞) D = [0;+∞)E = [0;+∞) ?

Слайд 31Функция y = arcsin x

у
х
0
-1
1
y = sin x
y = arcsin

Функция y = arcsin xух0-11y = sin xy = arcsin x

Слайд 32х
у
1
2
-1
-2
0
Функция у = arccos x
y = arccos x
y = cos

ху12-1-20Функция у = arccos xy = arccos xy = cos x

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей