Первообразная и интеграл

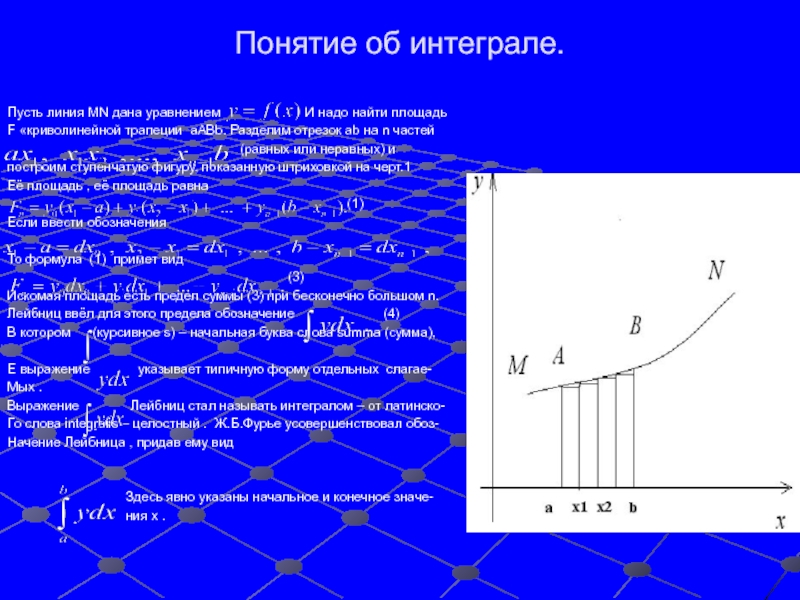
площадей , объемов и центров тяжести.
В зародышевой

форме такой метод применялся ещё Архимедом . Систе-
Матическое развитие он получил в 17-м веке в работах Кавальери ,Торриче-
лли, Фермам,Паскаля. В 1659 г. И.Барроу установил связь мемжду задачей
о разыскании площади и задачей о разыскании касательной. Ньютон и Лейб-
Ниц в 70-х годах 17-го века отвлекли эту связь от упомянутых частных геомет-
Рических задач. Тем мсамым была установлена связь между интегральным и
Дифференциальным исчислением.
Эта связь была использована Ньютоном , Лейбницем и их учениками для
Развития техники интегрирования. Своего нынешнего состояния методы интег-
Рирования в основном достигли в работах Л.Эйлера. Труды М.В.Остроградско-
Го и П.Л.Чебышева завершили развитие этих методов.

И надо

найти площадь
F «криволинейной трапеции aABb. Разделим отрезок ab на n частей
(равных или неравных) и
построим ступенчатую фигуру, показанную штриховкой на черт.1
Её площадь , её площадь равна
(1)
Если ввести обозначения

То формула (1) примет вид
(3)
Искомая площадь есть предел суммы (3) при бесконечно большом n.
Лейбниц ввёл для этого предела обозначение (4)
В котором (курсивное s) – начальная буква слова summa (сумма),

Е выражение указывает типичную форму отдельных слагае-
Мых .
Выражение Лейбниц стал называть интегралом – от латинско-
Го слова integralis – целостный . Ж.Б.Фурье усовершенствовал обоз-
Начение Лейбница , придав ему вид


Здесь явно указаны начальное и конечное значе-
ния x .

– переменной величиной.

Тогда интеграл

будет функцией от b .

Дифференциал этой функции равен

есть производная от функции

,

Т.С. Есть дифференциал функции :




Тогда функция называется первообразной для функции

есть первообразная от


Т.С.

Есть дифференциал функции





Функция является первообразной для функции

первообразной функции.
Неопределённый интеграл выражения

обозначается


Выражение

называется подинтегральным выражением,

Функция -подинтегральной функцией , переменная x –перемен-
Ной интегрирования. Разыскание неопределённого интеграла данной
Функции называется интегрированием.

есть . Эта функция является

Неопределённым интегралом выражения :




Где .

5)



2) 6)



3)

7)

4)

6)


2)

3)

4)

5)