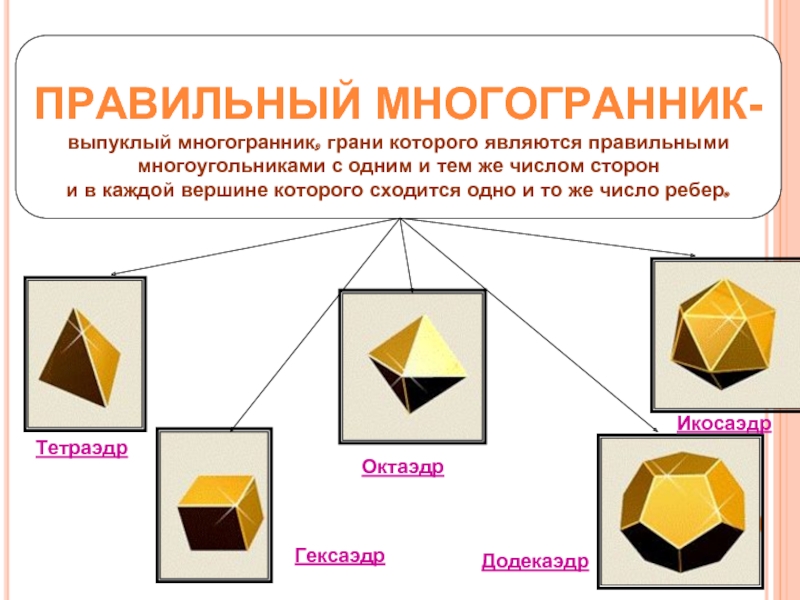
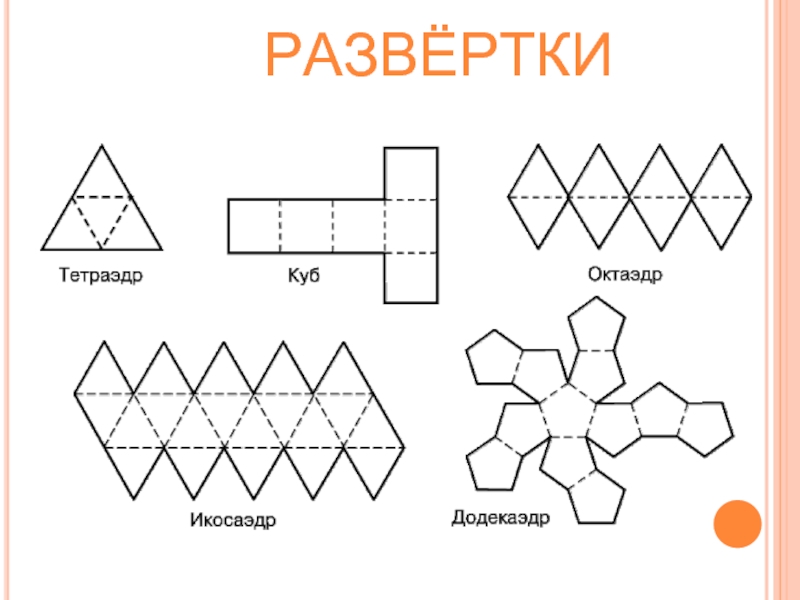
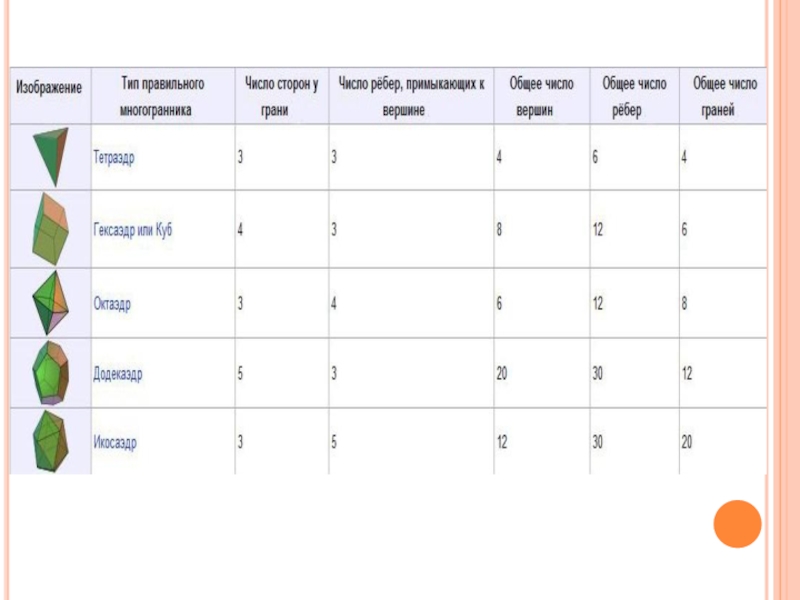
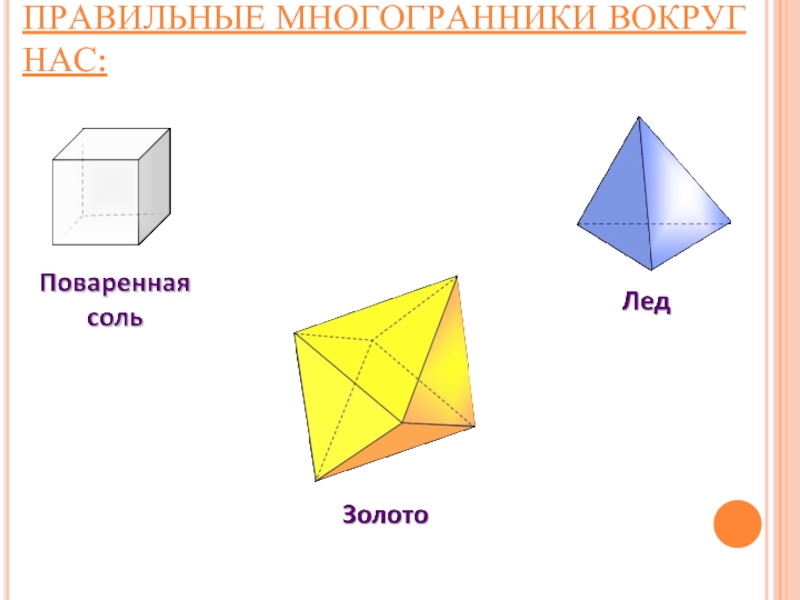
Правильные многогранники

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ НАЗЫВАЮТ ТАКЖЕ ТЕЛАМИ ПЛАТОНА.
Платон считал, что мир строится

из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

Платон
428 – 348 г. до н.э

и тем же числом сторон
и в каждой вершине которого

сходится одно и то же число ребер.

Гексаэдр

Тетраэдр

Октаэдр

Додекаэдр

Икосаэдр

- 8

«икоса» - 20

«додека» - 12

равносторонних треугольников, сходящихся в каждой вершине по три.
ТЕТРАЭДР

квадратных граней, сходящихся в каждой вершине по три.
КУБ (ГЕКСАЭДР)

граней, сходящихся в каждой вершине по четыре.

ОКТАЭДР

сходящихся в вершинах по три.

ДОДЕКАЭДР

двадцати равносторонних треугольников, сходящихся в каждой вершине по пять.

ИКОСАЭДР

проходящая через середины двух противоположных ребер, является его осью симметрии.

Плоскость α, проходящая через ребро АВ перпендикулярно к противоположному ребру CD правильного тетраэдра ABCD, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.

его диагоналей. Прямые a и b, проходящие соответственно через центры

противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии.

имеют центр симметрии и несколько осей и плоскостей симметрии.
1
2
3