Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку на тему: "Координаты вектора" 9 класс
Содержание
- 1. Презентация к уроку на тему: "Координаты вектора" 9 класс
- 2. Домашнее задание:П 87 – учить понятия, свойства№
- 3. 10.11.2016 Координаты вектора
- 4. Если векторы a и b коллинеарны и
- 5. В прямоугольной системе координат отложим от точки
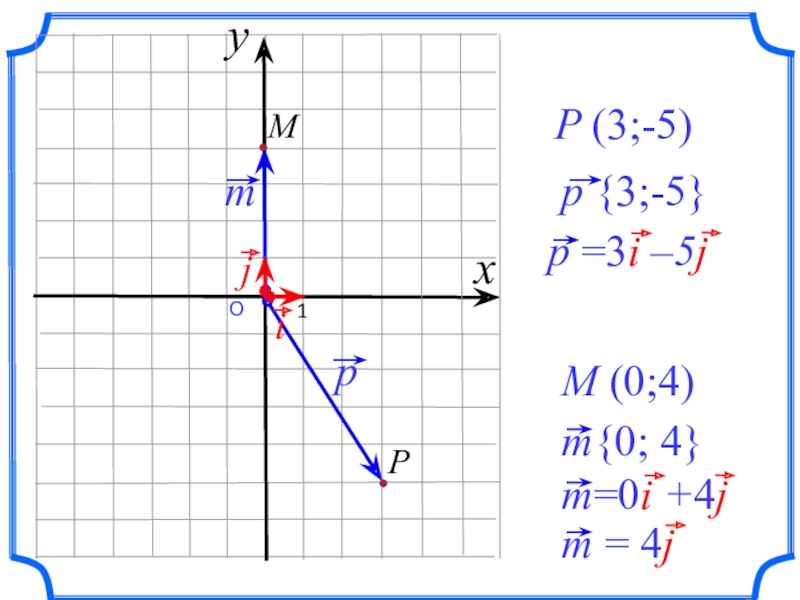
- 6. О 1P (3;-5)M (0;4)xy
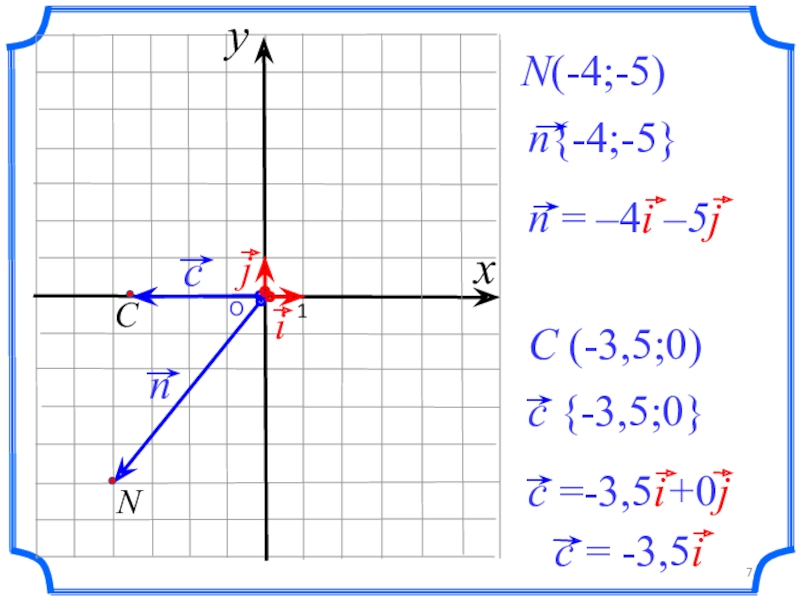
- 7. О 1N(-4;-5)C (-3,5;0)xy
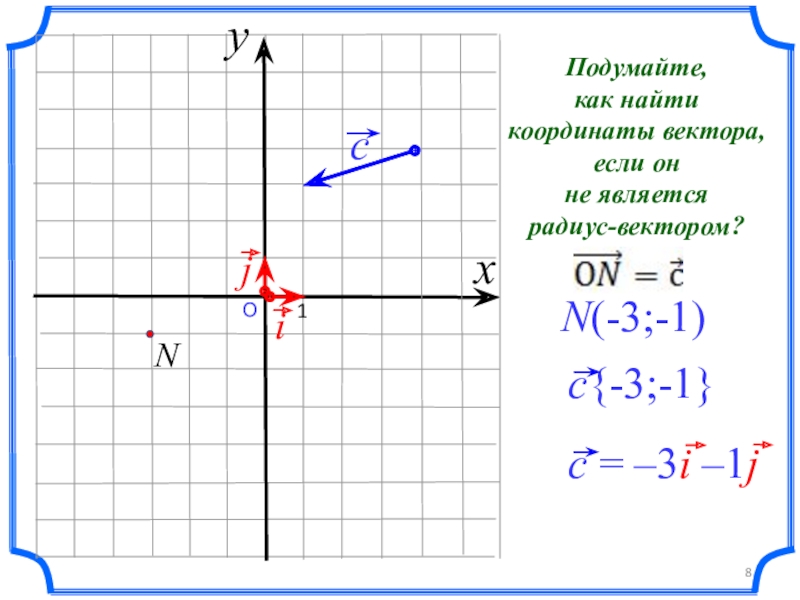
- 8. О 1N(-3;-1)xyПодумайте, как найти координаты вектора, если он не является радиус-вектором?
- 9. Свойства:Если векторы a = xi + yj
- 10. Каждая координата произведения вектора на число равна
- 11. ????????
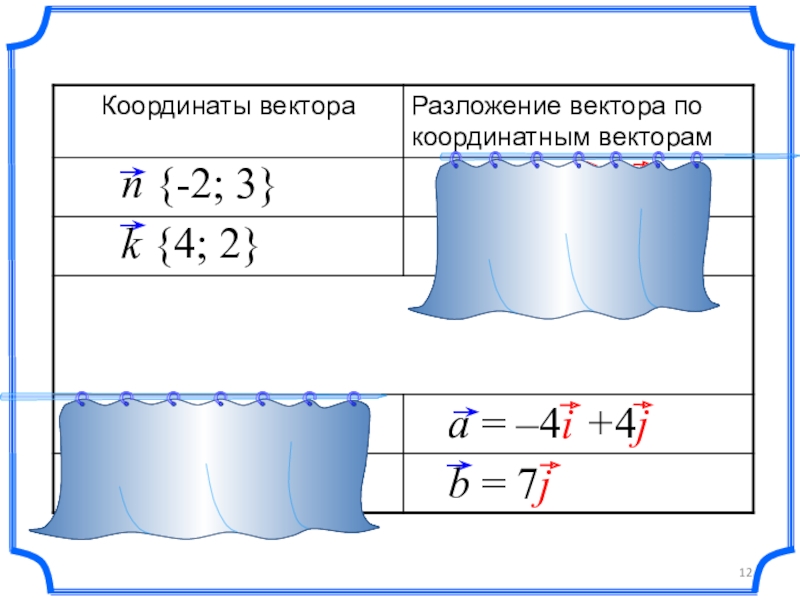
- 12. Слайд 12
- 13. О 1xy
- 14. yО6xАВС8Решение:Теорема Пифагора:a2 + b2 = c2
- 15. Скачать презентанцию
Домашнее задание:П 87 – учить понятия, свойства№ 6, № 8 – рабочая тетрадь№ 918, № 926 (б, г)
Слайды и текст этой презентации
Слайд 4Если векторы a и b коллинеарны и a ≠ 0,
то существует такое число k, что b = ka
Пусть a
и b – два данных вектора. Если вектор p представлен в виде p = xa + yb, где x и y – числа, то говорят вектор p разложен по векторам a и b.Числа x и y называются коэффициентами разложения.
Любой вектор можно разложить по двум неколиннеарным векторам, причем коэффициенты разложения единственны
Слайд 5В прямоугольной системе координат отложим от точки О единичные векторы
i и j
Векторы i и j называются координатными
векторами.i ↑↑Ox, │i│=1; j↑↑Oy, │j│=1
p = xi + yj
p {x; y} – где x, y координаты вектора p
Например:
ОА = 4i + 5j =>
ОВ = -6i + 2j =>
c = 5i – 3j =>
0 = o∙ i + o∙ j =>
ОА {4; 5}
OB {-6; 2}
c {5; -3}
0 {0; 0}
ОА – радиус-вектор
Слайд 9Свойства:
Если векторы a = xi + yj и b =
ki + lj равны, то x = k и y
= l. Координаты равных векторов соответственно равны.Каждая координата суммы двух или векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности двух или векторов равна разности соответствующих координат этих векторов.