Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку по теме "Квадратные уравнения"
Содержание
- 1. Презентация к уроку по теме "Квадратные уравнения"
- 2. КВАДРАТНЫЕ УРАВНЕНИЯ
- 3. Виды
- 4. Получение корней
- 5. Слайд 5
- 6. Геометрический смыслГрафиком квадратичной функции является парабола. Решениями
- 7. Одна точка пересеченияЕсли парабола пересекается с осью
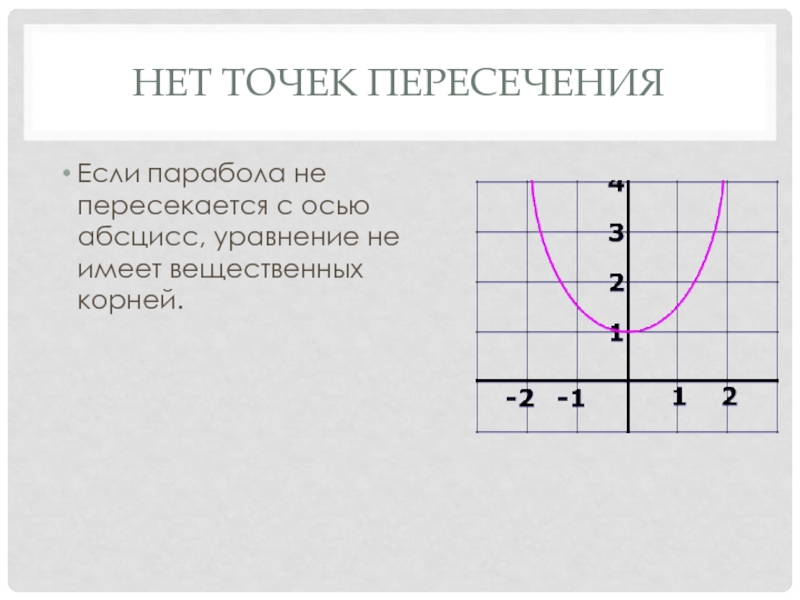
- 8. Нет точек пересеченияЕсли парабола не пересекается с осью абсцисс, уравнение не имеет вещественных корней.
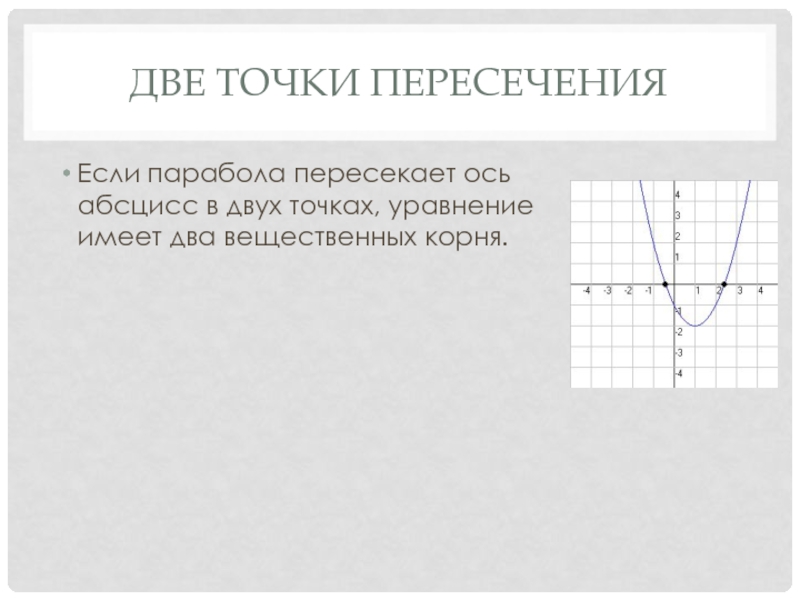
- 9. Две точки пересеченияЕсли парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.
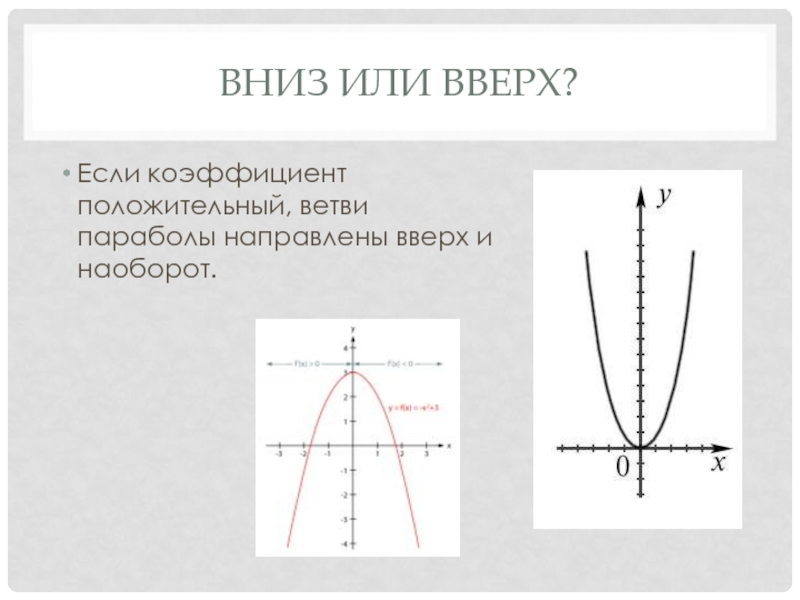
- 10. Вниз или вверх?Если коэффициент положительный, ветви параболы направлены вверх и наоборот.
- 11. Графический способ решения квадратных уравнений
- 12. Решение неполных квадратных уравнений
- 13. Решение неполных квадратных уравнений
- 14. Решение неполных квадратных уравнений
- 15. Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту
- 16. Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю
- 17. Теорема виетаРазность корней приведённого квадратного уравнения
- 18. РазложениеЕсли известны оба корня квадратного трёхчлена, его можно разложить по формуле
- 19. Спасибо за внимание!
- 20. Скачать презентанцию
КВАДРАТНЫЕ УРАВНЕНИЯ
Слайды и текст этой презентации
Слайд 1Презентация к уроку алгебры
Учителя математики гимназии 96 г.Казани
Бухараевой Ларисы юрьевны
Квадратные
уравнения.
Слайд 6Геометрический смысл
Графиком квадратичной функции является парабола. Решениями квадратного уравнения называют
абсциссы точек пересечения параболы с осью абсцисс.
Слайд 7Одна точка пересечения
Если парабола пересекается с осью абсцисс в одной
точке (в вершине параболы), уравнение имеет один вещественный корень.
Слайд 8Нет точек пересечения
Если парабола не пересекается с осью абсцисс, уравнение
не имеет вещественных корней.
Слайд 9Две точки пересечения
Если парабола пересекает ось абсцисс в двух точках,
уравнение имеет два вещественных корня.
Слайд 15Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного
члена равна второму коэффициенту
Слайд 17Теорема виета
Разность корней приведённого квадратного уравнения
равна коэффициенту p , а частное
корней равно свободному члену q.X1-x2=p
X1*x2=q
Пример:
Проверка