Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация- реферат на тему: "Золотое сечение" работа ученика 9 класса Демидова Василия.
Содержание
- 1. Презентация- реферат на тему: "Золотое сечение" работа ученика 9 класса Демидова Василия.
- 2. Учащийся 9-а класса Демидов ВасилийУчитель математики Еремеева Нина Никифоровна2009 годМОУ Новоаганская средняя школа №2
- 3. Цель работы:изучение истории развития «золотого сечения», его
- 4. Задачи 1. Более подробно рассмотреть понятие «золотое
- 5. Пропорция ( от лат. proportio)
- 6. Деление отрезка «золотым сечением» Золотое сечение (золотая
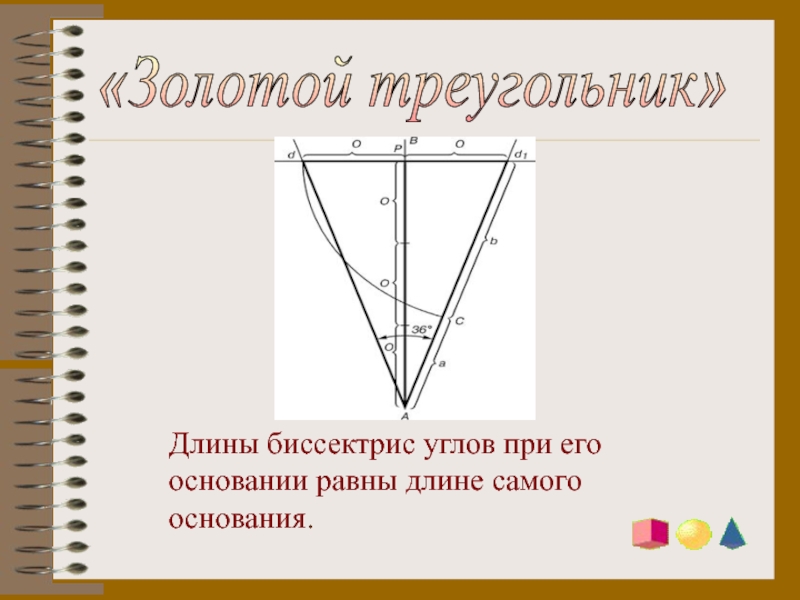
- 7. Длины биссектрис углов при его основании равны длине самого основания.«Золотой треугольник»
- 8. Слайд 8
- 9. Каждый конец пятиугольной звезды представляет собой “золотой”
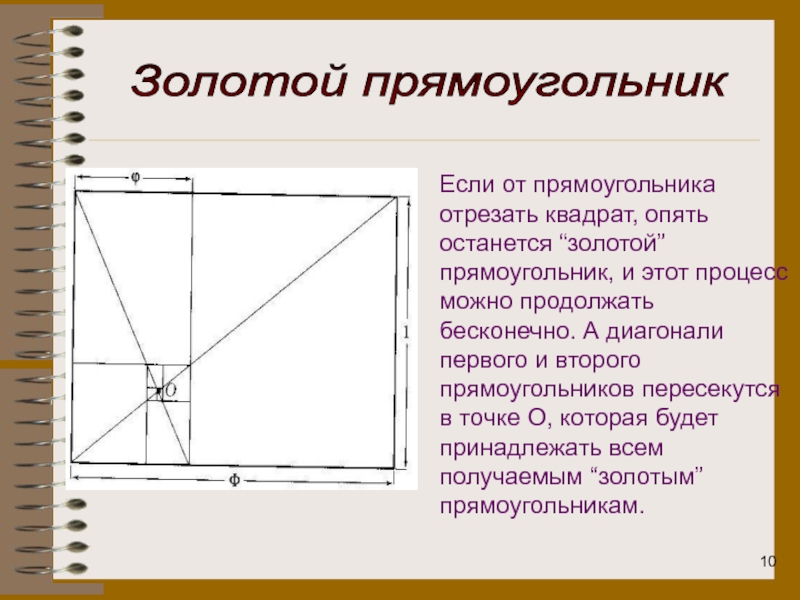
- 10. Если от прямоугольника отрезать квадрат, опять останется
- 11. «Природа говорит языком математики: буквы этого языка
- 12. Семечки в подсолнухе закручены слева направо и
- 13. Рассматривая расположение листьев на стебле растений, можно
- 14. Из всего сказанного можно сделать выводы:
- 15. «Золотое сечение» с давних пор привлекало и
- 16. Исследования А.Цейзинга Немецкий профессор Цейзинг в
- 17. Голова и «Золотое сечение» Золотое сечение
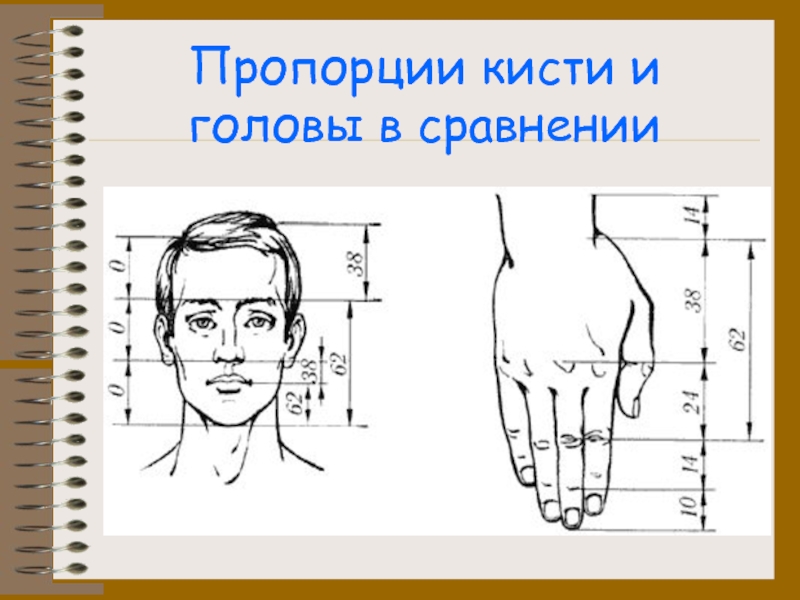
- 18. Пропорции кисти и головы в сравнении
- 19. Пропорции различных частей нашего тела составляет число
- 20. Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер
- 21. Творения великих умов прошлого, исследования
- 22. Слайд 22
- 23. Отношение периода спада к периоду роста почти
- 24. Молекулы
- 25. Античные храмы Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
- 26. На рисунках виден целый ряд закономерностей, связанных
- 27. «Золотое сечение» в пирамиде Хеопса
- 28. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта
- 29. «Пропорция обретается не только в числах
- 30. Слайд 30
- 31. ЛитератураВ.В. Зарудко. - «Золотое сечение. Традиция
- 32. Спасибо за внимание!
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Учащийся 9-а класса
Демидов Василий
Учитель математики
Еремеева
Нина Никифоровна
2009 год
МОУ
Новоаганская средняя школа №2
Слайд 3Цель работы:
изучение истории развития «золотого сечения», его места в современном
мире и современной науке.
дать наиболее полное
представление о данной теме;
Слайд 4Задачи
1. Более подробно рассмотреть понятие «золотое сечение», история происхождения,
алгебраическое нахождение «золотого сечения», геометрическое построение «золотого сечения».
2. Рассмотреть применение
«золотого сечения» в архитектуре Древней Греции.3. Рассмотреть «золотое сечение» как гармоническую пропорцию.
4. Изучить такие понятия как «золотой треугольник».
5. Постараться найти в окружающем меня мире применение этих понятий.
Задачи
Слайд 5
Пропорция ( от лат. proportio) соразмерность;
в математике
равенство между
двумя отношениями четырех величин.
Одним из видов пропорции является «Золотое сечение» или «Золотая пропорция».Что такое «пропорция»?
Слайд 6
Деление отрезка «золотым сечением»
Золотое сечение (золотая пропорция, деление в
крайнем и среднем отношении, гармоническое деление, φ) — деление отрезка
на части в таком соотношении, при котором большая часть относится к меньшей, как сумма к большей. Например, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ
Слайд 8
С золотой пропорцией
связан звездчатый пятиугольник.
Пятиконечной звезде около 3000 лет. Неудивительно, что
Пифагор сделал звездчатый пятиугольник, вписав его в выпуклый пятиугольник символом жизни и здоровья, а также тайным опознавательным знаком. В Средние века пентаграмма «предохраняла» от нечистой силы Звёздчатый пятиугольник
Слайд 9Каждый конец пятиугольной звезды представляет собой “золотой” треугольник. Его стороны
образуют угол 36° при вершине, а основание, отложенное на боковую
сторону, делит её в пропорции золотого сечения.Пятиконечная звезда
Слайд 10
Если от прямоугольника отрезать квадрат, опять останется “золотой” прямоугольник, и
этот процесс можно продолжать бесконечно. А диагонали первого и второго
прямоугольников пересекутся в точке О, которая будет принадлежать всем получаемым “золотым” прямоугольникам.Золотой прямоугольник
Слайд 11«Природа говорит языком математики: буквы этого языка – круги, треугольники
и иные математические фигуры» подтверждаются многими практическими работами в действительности.
Г.Галилео
Слайд 12
Семечки в подсолнухе закручены слева направо и наоборот. Отношение количества
спиралей в том и другом направлении равно 0,6.
У растений семейства
Сложноцветных цветы расположены в соцветии по спирали. «ЗОЛОТАЯ СПИРАЛЬ» В ПРИРОДЕ
Слайд 13
Рассматривая расположение листьев на стебле растений, можно заметить, что между
каждыми двумя парами листьев, третья расположена в месте золотого сечения.
Золотое
сечение в ботанике Слайд 14
Из всего сказанного можно сделать выводы:
во-первых, золотое сечение –
это один из основных основополагающих принципов природы;
во-вторых, человеческое представление
о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе. Слайд 15«Золотое сечение» с давних пор привлекало и внимание биологов. В
наши дни установлено «использование» золотой пропорции в организации структур биомолекул,
биоритмов мозга человека, членении конечностей человека, млекопитающих, птиц инасекомых, гармонической соразмерности частей тела человека и др.
Слайд 16Исследования А.Цейзинга
Немецкий профессор Цейзинг в середине 18 столетия
проделал огромную работу: он измерил более 2000 тел и высказал
предположение, что золотое сечение выражает среднестатистический закон: деление тела точкой пупа – один из основных показателей золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.Слайд 17Голова и «Золотое сечение»
Золотое сечение является основой построения
гармоничных форм, так как является абсолютным законом формообразования в природе,
частью которой мы являемся. Таким образом голова человека тоже проявляет пропорции золотого сечения.Слайд 19Пропорции различных частей нашего тела составляет число очень близкое к
золотому сечению. Если эти пропорции совпадают с формулой золотого сечения,
то внешность или тело человека считается идеально сложенным.Примерами золотого сечения в строении тела человека являются:Расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618
Расстояние от уровня плеча до макушки головы и размера головы равно 1:618
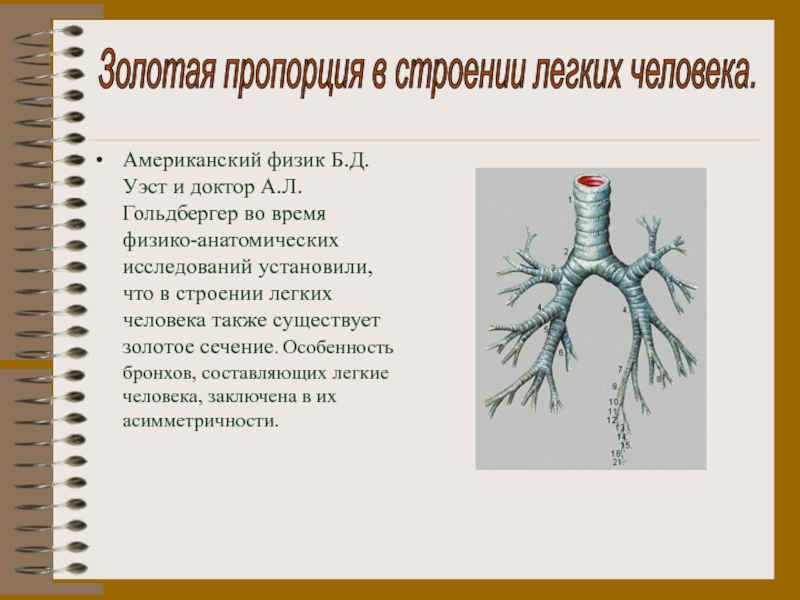
Слайд 20Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических
исследований установили, что в строении легких человека также существует золотое
сечение. Особенность бронхов, составляющих легкие человека, заключена в их асимметричности.Золотая пропорция в строении легких человека.
Слайд 21 Творения великих умов прошлого, исследования современности
убедительно доказывают,
что по принципу «золотого сечения» создана вся Вселенная. Вполне возможно, что в недалёком будущем кто-то отыщет новые закономерности,
основывающиеся на золотой пропорции…
Слайд 23Отношение периода спада к периоду роста почти не отличается от
золотой пропорции!
астрономические
данные свидетель- ствуют о том, что активность Солнца подчиняется закону золотого сечения... Многочисленные
7/4,2 = 1,667
Значит и огромная масса земных явлений, обусловленных солнечно-земными связями, также следует этому закону.
Слайд 24 Молекулы ДНК
В биологических исследованиях
70-90 гг. показано, что, начиная с вирусов и растений и
кончая организмом человека, наблюдается соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.Слайд 25Античные храмы
Одним из красивейших произведений древнегреческой архитектуры является Парфенон
(V в. до н. э.).
Слайд 26На рисунках виден целый ряд закономерностей, связанных с золотым сечением.
Пропорции здания можно выразить через различные степени числа Ф=0,618...
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по золотому сечению, то получим те или иные выступы фасада.Слайд 28Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из
гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления
при их создании .«Золотое сечение» в пирамиде Хеопса
Слайд 29 «Пропорция обретается не только в числах и мерах, но
также в звуках, тяжестях, временах и положениях и в любой
силе, какая бы она ни была».Леонардо да Винчи
Вместо заключения
Слайд 30
Пифагор
Принято считать, что понятие
о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Слайд 31
Литература
В.В. Зарудко. - «Золотое сечение. Традиция и современность». -2003.-
Москва. – Издательство «Наука». – 211стр. – Монография.
Ю.В. Келдыш.
– Музыкальная энциклопедия. – Издательство «Советская энциклопедия». – Москва. – 1974г. – стр.958.3. А.А. Соколов. - «Тайны Золотого сечения» - «Техника молодежи». - №5. – 1978г. – Типография «Молодая гвардия». – Москва. – 63стр.
4. Г.Н. Соловьева. –«Альбрехт Дюрер. Трактаты, дневники, письма.» – Санкт-Петербург. – Издательство «Азбука». – 2000г. – 662стр
5. В.С. Смирнов. –– «Золотое сечение – основа математики и физики будущего. Спираль развития Вселенной». Санкт – Петербург. – Типография ИПТ. – 113стр. – 1997г.
6. Ю.В.Прохоров. - Большой энциклопедический словарь.-Научное издательство «Большая Российская Энциклопедия»-стр.846.-Москва-2000г.
7. Энциклопедия для детей.- «Аванта+».-Математика.-685стр.-Москва.-1998г.
8. В.Д.Цветков. – «Сердце, золотое сечение и симметрия». – Пущино. – типография ОНТИ ПНЦ РАН - 1997г. – 169стр.
9. А.И. Щетников. – «Пифагорейское учение о числе и величине». – Новосибирск. – Артель «Напрасный труд». – 2002г. – стр.47.