Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
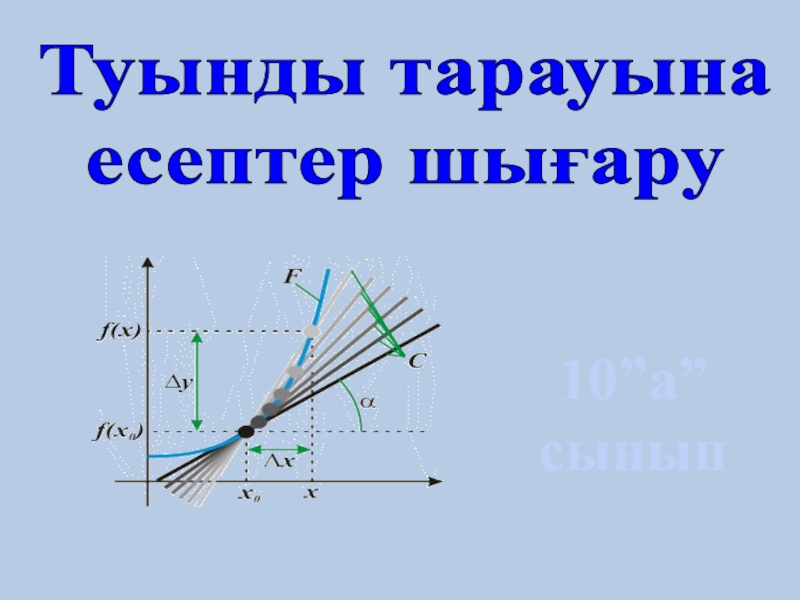
Применение производной к исследованию функций
Содержание
- 1. Применение производной к исследованию функций
- 2. СОДЕРЖАНИЕ.Задания на соответствие.Математическое лото.Устные задания.
- 3. Угловым коэффициентом прямой называетсяk = sin k
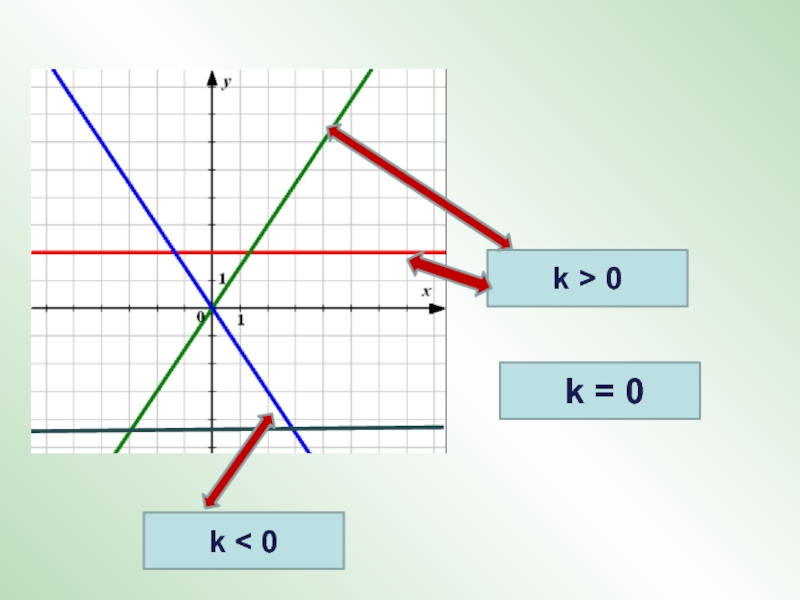
- 4. k = 0k > 0k < 0
- 5. Для каждой линейной функции найдитекоэффициент k.
- 6. Геометрический смысл производной состоит в том, что
- 7. f ' (х) < 0f ' (х)
- 8. Стационарными называют точки, в которых производная функциибольше 0равна 0больше 1меньше 0
- 9. Если при переходе через стационарную точку х0
- 10. Слайд 10
- 11. Непрерывная функция у = f(x)
- 12. Непрерывная функция у = f(x)
- 13. y = f /(x)1 2
- 14. На рисунке изображен график производной функции у
- 15. y = f /(x) Функция
- 16. На рисунке изображён график функции
- 17. 1 2 3 4
- 18. В какой из указанных точек производная функции, график которой изображен на рисунке, отрицательна?х3хух4 х2 х1
- 19. .На рисунке изображены прямые , являющиеся касательными
- 20. Непрерывная функция у = f(x)
- 21. На рисунке изображен график функции у =f(x)
- 22. Угол наклона касательной с осью Ох тупой,
- 23. -4 -3 -2
- 24. Диагностическая работа №1.Диагностическая работа №2.
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Применение производной к исследованию функций.
Чугуева Любовь
Николаевна. Учитель математики МБОУ СОШ №59 п. Белозёрный.
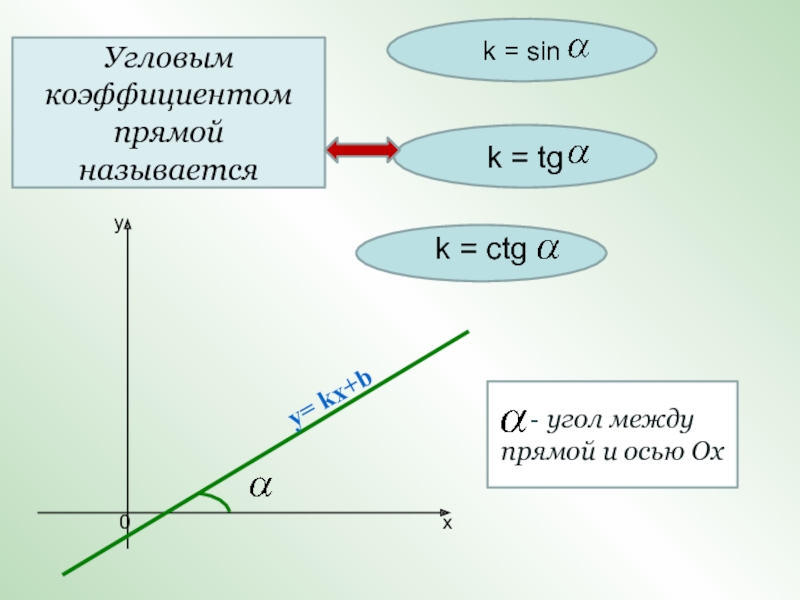
Слайд 3Угловым коэффициентом прямой называется
k = sin
k = tg
k
= ctg
- угол между прямой и осью Ох
y= kx+b
Слайд 6Геометрический смысл производной состоит в том, что значение производной функции
f(х) в точке х0 равно
угловому коэффициенту
касательной к графику
функцииу = f(х) в точке
(х0; f(х0)).
нулю.
f ' (х)= k= tg
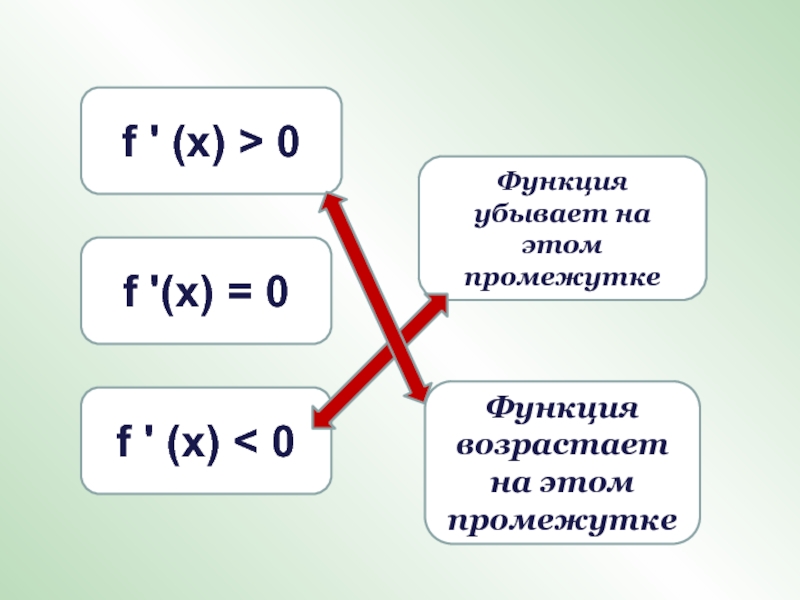
Слайд 7f ' (х) < 0
f ' (х) > 0
Функция убывает
на этом промежутке
f '(х) = 0
Функция возрастает на этом промежутке
Слайд 9Если при переходе через стационарную точку х0
изменяет знак
с «–»
на «+»;
изменяет знак с «+»
на «-»;
не изменяет
свой знак В точке хо экстремума нет
В точке хо - минимум
В точке хо - максимум
Слайд 11 Непрерывная функция у = f(x) задана на отрезке
[a; b].
В ответе укажите количество точек графика этой функции,
в которых касательная параллельна оси Ох. y = f(x)
y
x
a
b
Слайд 12 Непрерывная функция у = f(x) задана на отрезке
[a; b].
На рисунке изображен график ее производной у =
f/(x). В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f/(x)
y
x
a
b
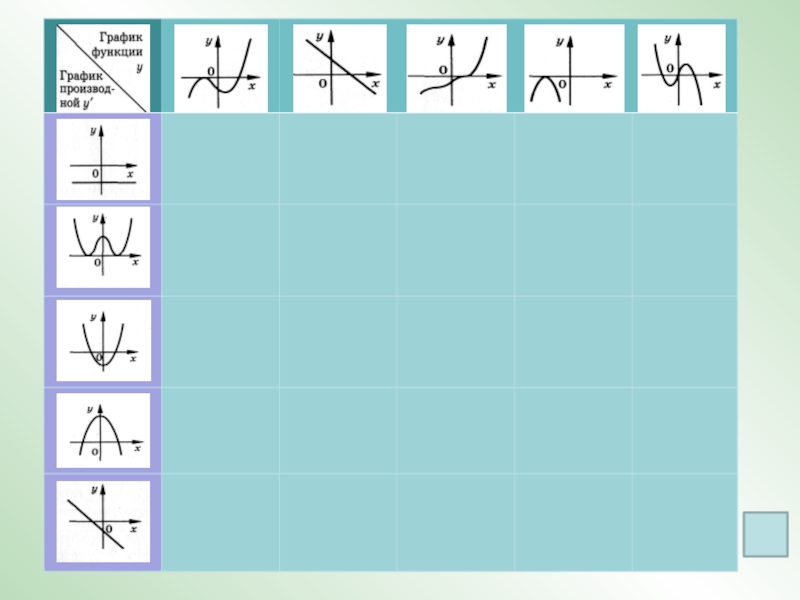
Слайд 13y = f /(x)
1 2 3 4
5 х
-4 -3 -2
-1
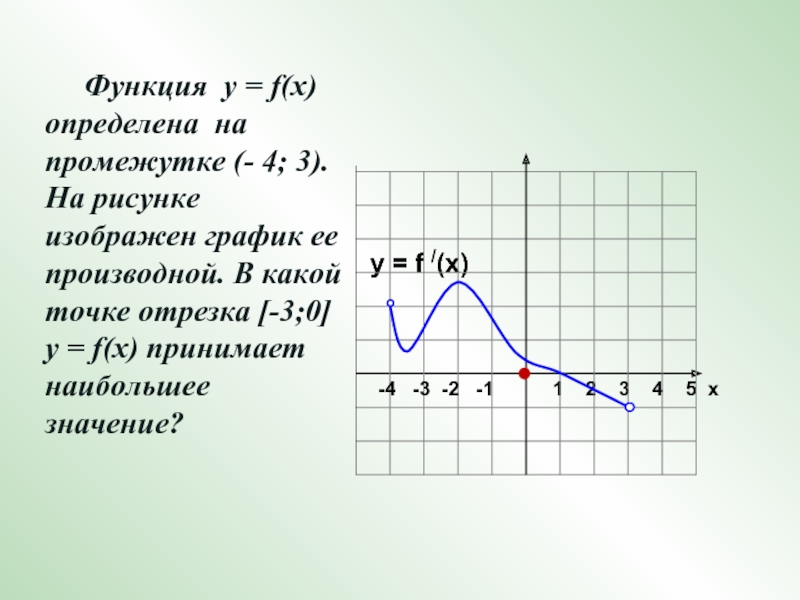
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. В какой точке отрезка [-3;0]
у = f(x) принимает наибольшее значение?
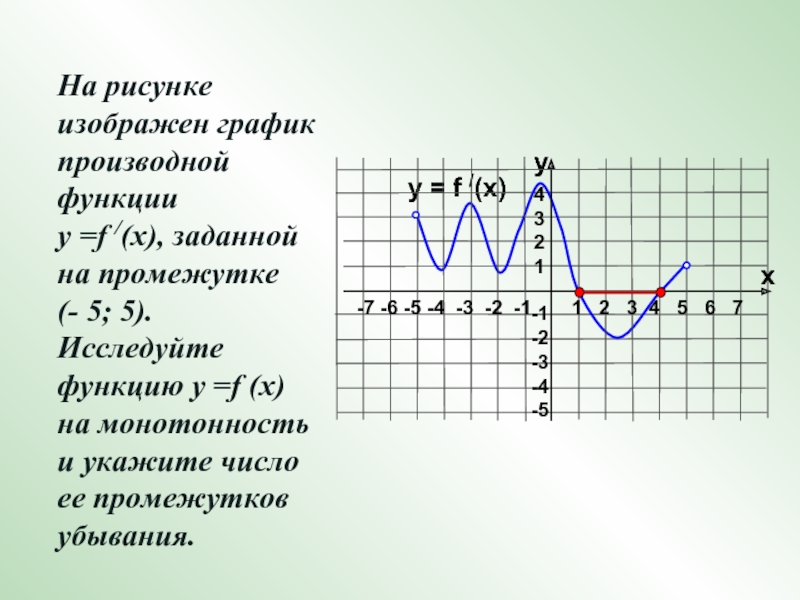
Слайд 14На рисунке изображен график производной функции
у =f /(x), заданной
на промежутке
(- 5; 5). Исследуйте функцию у =f (x)
на монотонность и укажите число ее промежутков убывания.y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Слайд 15y = f /(x)
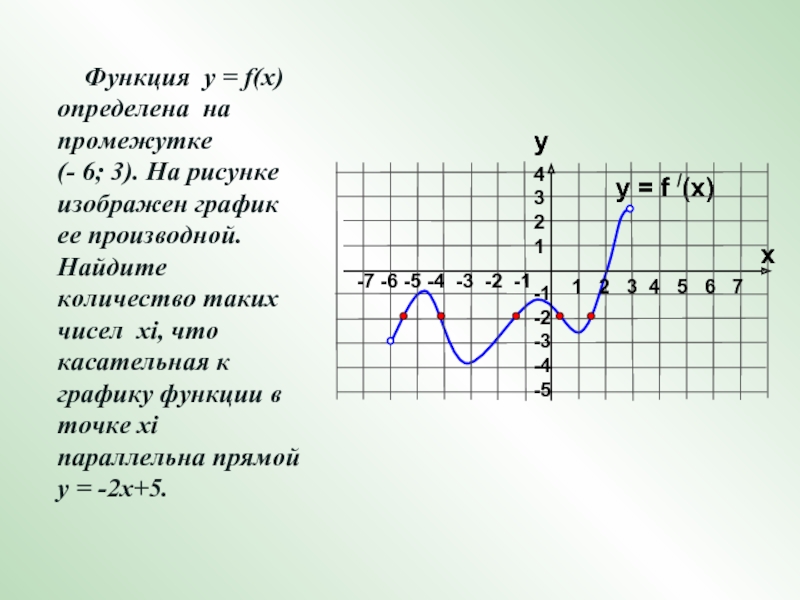
Функция у = f(x)
определена на промежутке
(- 6; 3). На рисунке изображен график
ее производной. Найдите количество таких чисел хi, что касательная к графику функции в точке хi параллельна прямой у = -2х+5.1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
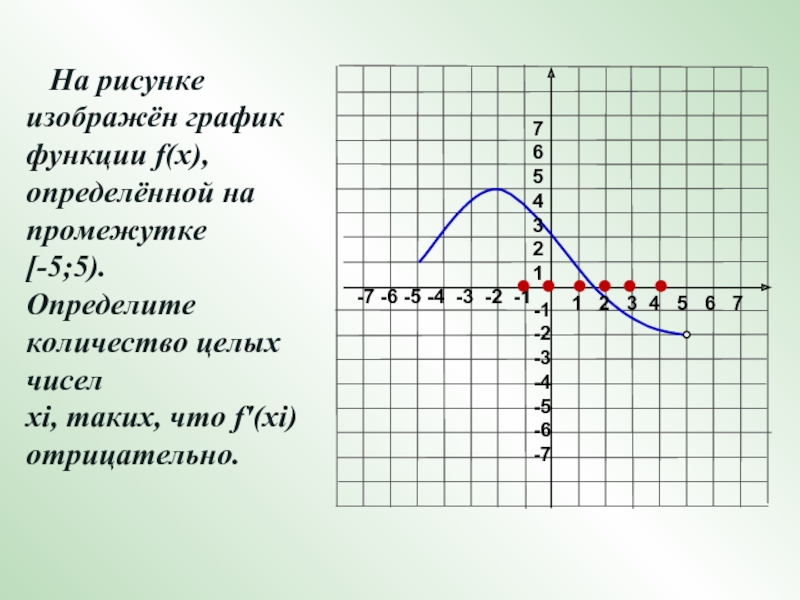
Слайд 16 На рисунке изображён график функции f(x), определённой на
промежутке
[-5;5).
Определите количество целых чисел
хi, таких, что f'(xi)
отрицательно. 1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Слайд 171 2 3 4 5 6
7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
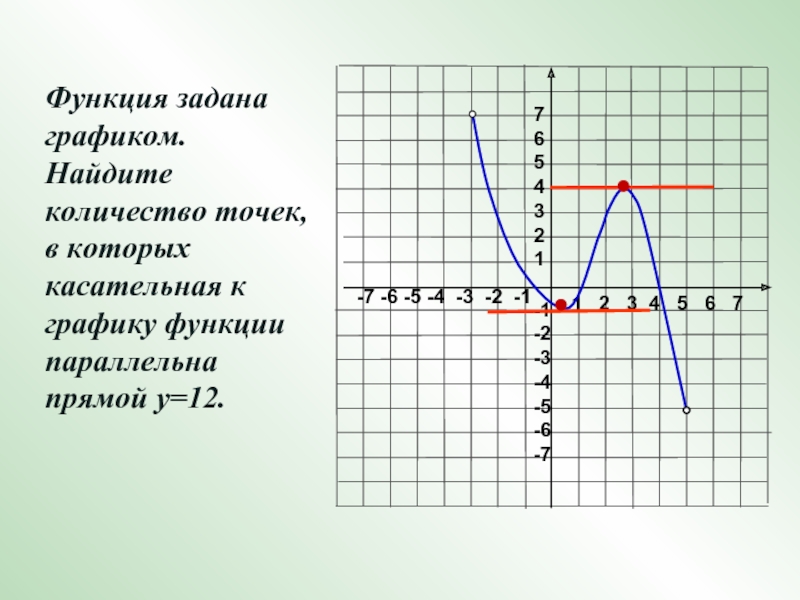
Функция задана графиком.
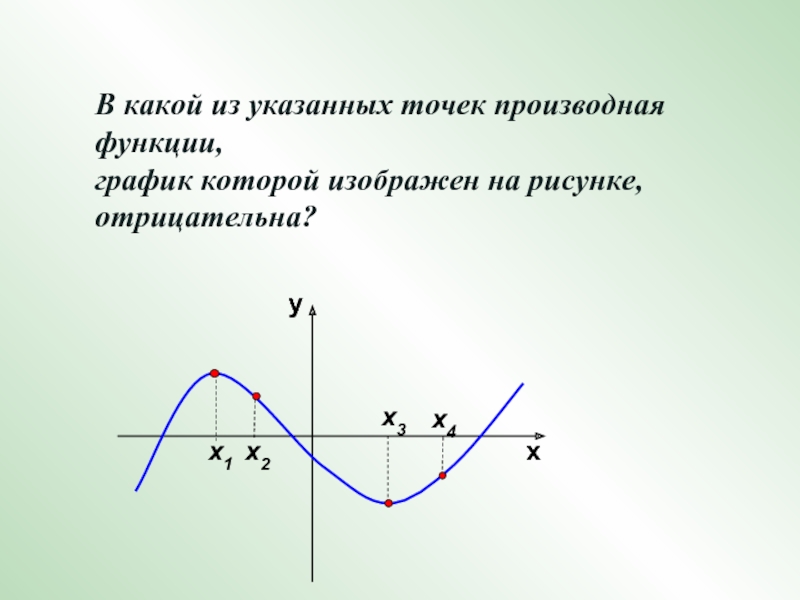
Найдите количество точек, в которых касательная к графику функции параллельна прямой у=12.Слайд 18В какой из указанных точек производная функции,
график которой изображен
на рисунке, отрицательна?
х3
х
у
х4
х2
х1
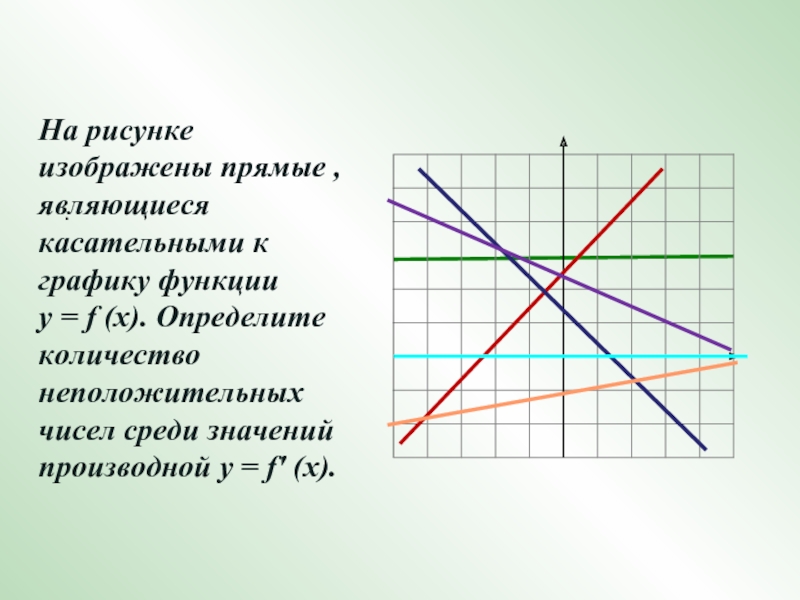
Слайд 19.
На рисунке изображены прямые , являющиеся касательными к графику функции
у = f (х). Определите количество неположительных чисел среди значений
производной у = f' (х).Слайд 20 Непрерывная функция у = f(x) задана на отрезке
[a;b].
На рисунке изображен график её производной. В ответе укажите
количество точек экстремума, количество точек минимума.y = f(x)
y
x
a
b
Слайд 21
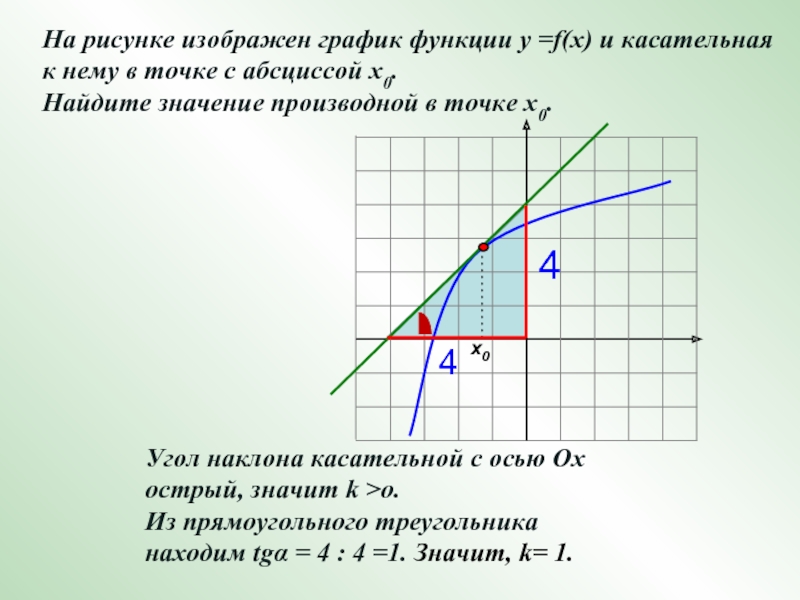
На рисунке изображен график функции у =f(x) и касательная к
нему в точке с абсциссой х0.
Найдите значение производной в
точке х0.х0
Угол наклона касательной с осью Ох острый, значит k >o.
Из прямоугольного треугольника
находим tgα = 4 : 4 =1. Значит, k= 1.
4
4
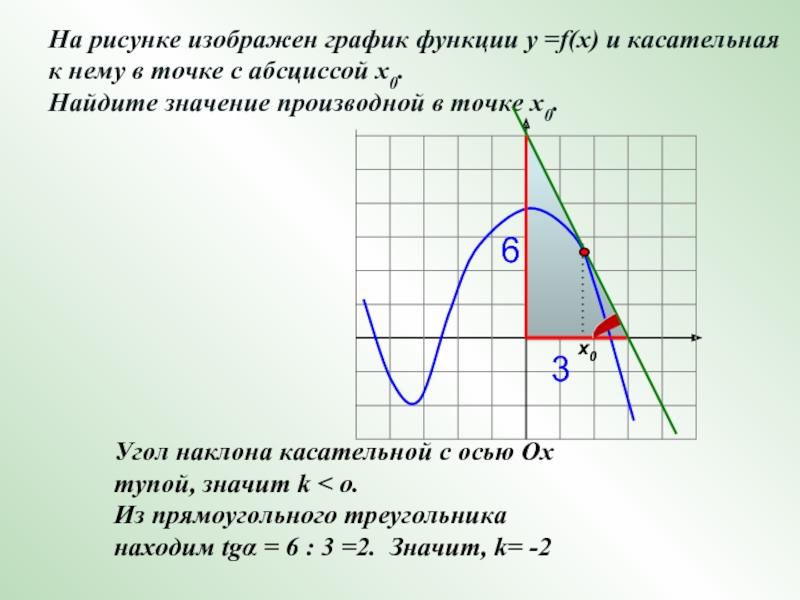
Слайд 22Угол наклона касательной с осью Ох тупой, значит k
o.
Из прямоугольного треугольника
находим tgα = 6 : 3 =2.
Значит, k= -2На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
х0
6
3
Слайд 23 -4 -3 -2 -1
1
2 3 4 5 х
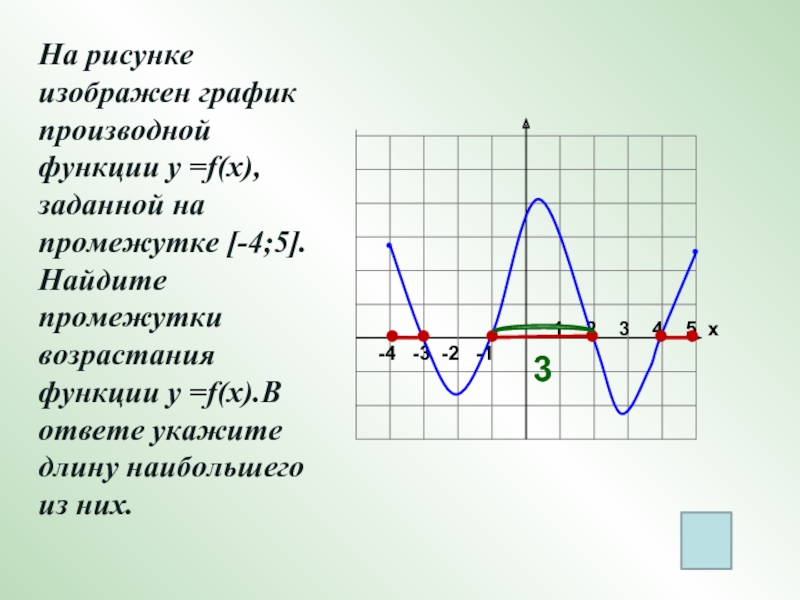
На рисунке изображен
график производной функции у =f(x), заданной на промежутке [-4;5]. Найдите промежутки возрастания функции у =f(x).В ответе укажите длину наибольшего из них.
3






![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a; b]. Непрерывная функция у = f(x) задана на отрезке [a; b]. В ответе укажите количество точек](/img/thumbs/c15ac9bc1bcb906a28078e7f5af5e3ad-800x.jpg)
![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a; b]. Непрерывная функция у = f(x) задана на отрезке [a; b]. На рисунке изображен график ее](/img/thumbs/563892d3fc710fd6d6fbd1a150a477b6-800x.jpg)
![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a;b]. На Непрерывная функция у = f(x) задана на отрезке [a;b]. На рисунке изображен график её производной.](/img/thumbs/ac29b1f3ac23a3de3823c1de5734d130-800x.jpg)