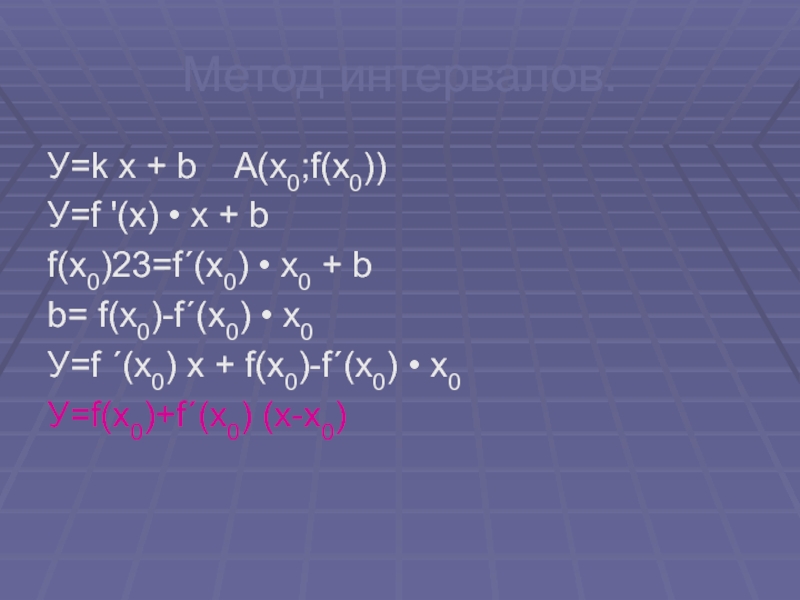Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная сложной функции 10 класс
Содержание
- 1. Производная сложной функции 10 класс
- 2. Содержание:Приращение функцииПонятие о производнойОпределение производной Правила вычисления производнойПроизводная сложной функцииПроизводные тригонометрических функций
- 3. Приращение функции.Δf=f(x0+ Δ x)-f(x0) конспект
- 4. Определение.Производной функции ƒ в точке х0 называется
- 5. Понятие о производной.(x2)΄= Δ у/ Δx=(x0+ Δx)2-x02/
- 6. Определение производной.f΄(x0)=lim /Δx →0f(x0+ Δx)-f(x0)/Δxf (x)-дифференцируемас΄=0; x΄=1; (c x)΄=c (x)΄= cДалее.
- 7. Правило вычисления производных.(u ± v ) ΄
- 8. Производная сложной функции.h ( x ) =
- 9. Слайд 9
- 10. Дифференцирование.Функцию, имеющую производную в точке хо называют
- 11. Приращение функции.При сравнении значения функции ƒ в
- 12. Приращение функции.Эта разность называется приращением Функции ƒ
- 13. Производная сложной функцииЕсли функция f имеет производную
- 14. Приращение функции.Пример 1.Найдем приращения Δ х и
- 15. Производная сложной функции.Пример 1.Найдем производную функцииh (x)=(2x+3)100Функцию
- 16. Правила вычисления производных. Правило 1.Если функции U
- 17. Правила вычисления производных.Пример 1. Найдем производные функций:А)
- 18. Производные тригонометрических функций.Формула производной синуса. Докажем, что
- 19. Производные тригонометрических функций.Для вывода формулы достаточно показать
- 20. Формула приближенного вычисления.У=f(x0)+f΄(x0)(x-x0)У ≈f(x0)+f '(x0) Δx
- 21. Производная в физике и технике.Vср (Δt)=Δx/Δt→v(t0)Δx/Δt→x'(t0)V (t)= x´(t) a=v' (t)
- 22. Метод интервалов.1f Δf →0 при Δ
- 23. Метод интервалов.У=k x + b A(x0;f(x0))У=f
- 24. Касательная к графику функции.k=f ´(x0)=tgαf ´(x1)>0; f ´(x2)=0; f ´(x3)
- 25. Касательная к графику функции.f (c)= f (b
- 26. Скачать презентанцию
Содержание:Приращение функцииПонятие о производнойОпределение производной Правила вычисления производнойПроизводная сложной функцииПроизводные тригонометрических функций
Слайды и текст этой презентации
Слайд 2Содержание:
Приращение функции
Понятие о производной
Определение производной
Правила вычисления производной
Производная сложной функции
Производные
тригонометрических функций
Слайд 4Определение.
Производной функции ƒ в точке
х0 называется число, к которому
стремится разностное отношение, при Δ х, стремящемся к нулю.
Конец.
Слайд 5Понятие о производной.
(x2)΄= Δ у/ Δx=(x0+ Δx)2-x02/ Δx=x20+2x Δx+
+Δx2-x02/ Δx=2x0
Δx+ Δx2/ Δx=2x0+Δx→2x0
↓0
Назад
Слайд 6Определение производной.
f΄(x0)=lim /Δx →0
f(x0+ Δx)-f(x0)/Δx
f (x)-дифференцируема
с΄=0; x΄=1; (c x)΄=c (x)΄=
c
Далее.
Слайд 7Правило вычисления производных.
(u ± v ) ΄ = u ΄±
v ΄
(u · v ) ΄ = u΄ v
+ u v ΄(u / v) ΄ =u ΄ v – u v ΄/ v2
(x n) ΄=n x n-1
Вперед.
Слайд 9
Производные тригонометрических функций.
(sin x) ΄ =cos x
(cos x) ΄ = - sin x
(tg x) ΄ = 1/cos2
(ctg x) ΄ = -1/sin2 x
h( x)=g ( f ( x ) )
h ΄ (x0)=g ΄ (f(x0))·f ΄ (x0)
Далее.
Слайд 10Дифференцирование.
Функцию, имеющую производную в точке хо называют дифференцируемой в этой
точке. Пусть D1-множество точек, в которых функция ƒ дифференцируема.Сопоставляя каждому
х € D1число ƒ ΄ (х), получим новую функцию с областью определения D1.Эта функция называется производной функцииy = ƒ (х).Мы получаем формулы (х3)=3х2
(х2)=2х,(kх +b) ΄ =k.В формуле k=0, b=С
где С произвольная постоянная получаем
что С΄ =0,производная постоянная равна нулю.
Слайд 11Приращение функции.
При сравнении значения функции ƒ в некоторой фиксированной точке
х0 значениями этой функции в различных
Точках х лежащих в
окрестности х0,удобно выражать разность ƒ (х)-ƒ (х0)Через разность х-х0,пользуясь понятиями «приращение аргумента»и
«приращение функции».
Δ х = х-х0 → х = х0+ Δ х.
Вследствие этого функции ƒ изменится на
Величину ƒ (х)- ƒ (х0)= ƒ (х0+ Δ х)-ƒ (х0).
Слайд 12Приращение функции.
Эта разность называется приращением
Функции ƒ в точке х0
соответствующим
приращению Δ х, и обозначается Δ ƒ ,
Т.е.по определению
Δ ƒ = ƒ (х0+ Δ х)- ƒ (х0),откуда
ƒ(х)= ƒ (х0+ Δ х)= ƒ (х0)+ Δ ƒ .
Обратите внимание :при фиксированном х0
Приращение Δ ƒ есть функция от Δ х.
Δ ƒ называют также приращением зависимой
Переменной и обозначают через Δ у для функции
У= ƒ (х).
ДАЛЬШЕ
Слайд 13Производная сложной функции
Если функция f имеет производную в точке х0,а
функция g имеет производную в точке у0=f(х0),то сложная
функция h(х)=g (f(х))
также имеет производную в точке х0,причемh΄(х0)=g΄(f(х0)) · f΄(х0).
Далее.
Слайд 14Приращение функции.
Пример 1.Найдем приращения Δ х и Δ f в
точке х0 ,если f(х)= Х2 ,А) Х0=2 и: Х=1,9;
Δ
х = х-х0=1,9-2= - 0,1;Δ f =f(1,9)-f(2)=1,92-22= - 0,39
НАЗАД
Слайд 15Производная сложной функции.
Пример 1.Найдем производную функции
h (x)=(2x+3)100
Функцию h можно представить
в виде сложной функции
h (x)=g (f (x)), где g (y)=y100,
y=f (x)=2x+3.Так как f ΄(x)=2 и g΄(y)=100y99, имеем
h΄(x)=2·100y99=200(2x+3)99
Назад.
Слайд 16Правила вычисления производных.
Правило 1.Если функции U и v дифференцируемое
в точке х0 ,то их сумма дифференцируема в этой точке
и производная суммы равна сумме производных.(U + v) ΄ = U΄ + v΄ .
Правило 2.Если функции u и v дифференцируемы в точке х0,то их произведение дифференцируемо в этой точке (u v ) ΄= u΄ v +u v΄.
Правило 3.Если функции u и v дифференцируемы в точке х0 и функции v не равна нулю в этой точке то
Частное u/ v также дифференцируемо в х0 и
(u/ v ) ΄ =(u΄ v- u v΄)/v2.
Далее.
Слайд 17Правила вычисления производных.
Пример 1. Найдем производные функций:
А) f (x)=x2-1/x
(1/x) ΄=
- x΄/x2= -1/x2, поэтому (x2- 1/x) ΄=
=(х2) ΄-(1/x) ΄=2x-(-1/x2)=2x+1/x2
Конец.
Слайд 18Производные тригонометрических функций.
Формула производной синуса. Докажем, что функция синуса имеет
производную в любой точке и (sin x) ΄= cos x.
Применяя
формулу sin α –sinβ=2cos α β/2 · sin α+β/2,
Находим
Δ sin x/ Δ x=sin(x0+Δ x)-sin x0/Δ x =
=2cos(x0+Δ x/2)sin Δx/2/ Δ x=
= sinΔx/2/Δx/2cos(x0+Δx/2).
Далее.
Слайд 19Производные тригонометрических функций.
Для вывода формулы достаточно показать ,что
а) sinΔx/2/Δx/2→ 1при
Δx→ 0;
б) cos(x0+Δx/2) → cos x0 при Δx→ 0
Опираясь на
эти утверждения, можно получить формулу. Действительно, при Δ х→0(x0+Δx/2) Δ Δ sin x/Δx=sinΔx/2/Δx/2Δ· cos →
→1· cos x0=cos x0.
Конец.
Слайд 23Метод интервалов.
У=k x + b A(x0;f(x0))
У=f '(x) • x
+ b
f(x0)=f´(x0) • x0 + b
b= f(x0)-f´(x0) • x0
У=f
´(x0) x + f(x0)-f´(x0) • x0У=f(x0)+f´(x0) (x-x0)
Слайд 24Касательная к графику функции.
k=f ´(x0)=tgα
f ´(x1)>0; f ´(x2)=0; f ´(x3)
´(x1)=1; f ´(x2)=0; f ´(x3)=-1
