Решение квадратных уравнений 8 класс

уравнений

Автор: Малыч Людмила Александровна
учитель математики МБОУ СОШ № 7
Станицы Степной Приморско-Ахтарского района

«Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий».
А. Моркушевич.

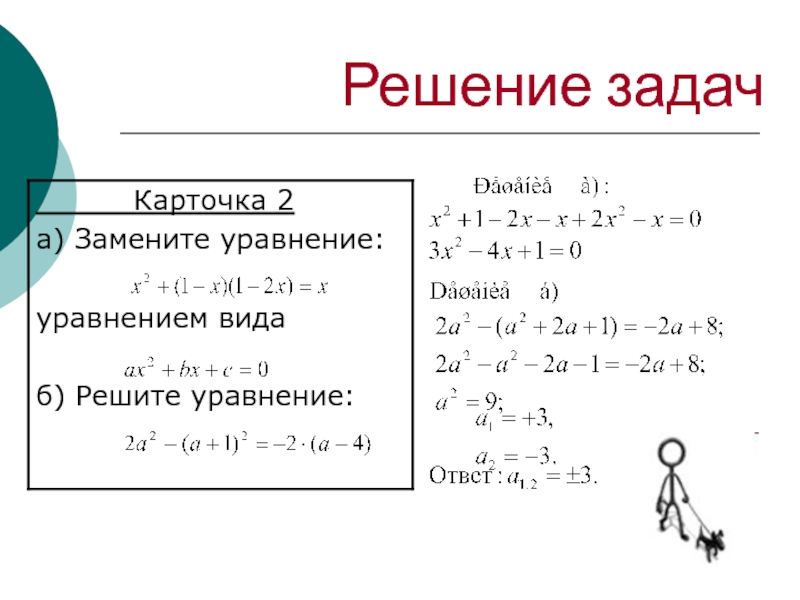
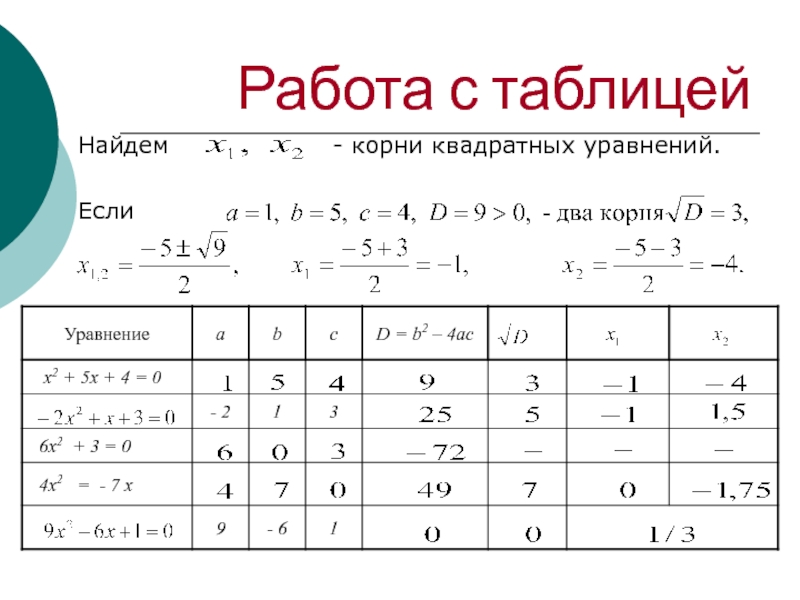
Решение квадратных

по формуле;
привитие аккуратности в работе.
повторение изученного материала;

квадратного уравнения и закрепить изученный материал решениями примеров.
3. Вырабатывать умение

слушать
ответы учителя и учащихся.

вида

где a,b,c – заданные числа,

а ≠ 0, х – неизвестное (независимая переменная) называется квадратным.

Является ли квадратным уравнение:

а)


б)

Как называются коэффициенты a, b, c ?

уравнения?

Уравнения

вида


где a,b,c – некоторые числа, отличные от нуля -
называются неполными квадратными
уравнениями.

Как решается уравнение где d > 0 ?

(сообщение).

Неполные квадратные уравнения и частные

виды полных квадратных уравнений умели решать вавилоняне (примерно за 2 тысячи лет до новой эры). Некоторые виды квадратных уравнений решали древнегреческие математики, сводя их решение к геометрическим построениям. Правило решения квадратных уравнений, приведённых к виду

где а > 0, дал индийский учёный Брахмагупта (VII в.). Вывод формулы корней квадратного уравнения в общем виде имеется у Виетта, однако он признавал только положительные корни. Итальянские математики XVI в. учитывают помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.

решения, который позволит быстро находить корни квадратного уравнения.
Попробуем это сделать

в процессе выполнения
математического диктанта.


Будьте предельно внимательны,
старайтесь сделать всё сами!!!

на 4а;
2. Перенесём свободный член вправо:

3. Дополним

левую часть уравнения до полного квадрата, для чего к обеим частям уравнения прибавим по


следовательно,

то, используя известную
теорему,

имеем: откуда


Мы получили формулу для вычисления корней квадратного уравнения. Сколько всего корней ?

Введём обозначение это число – дискриминант квадратного уравнения. Тогда формула корней принимает вид:


где b, a – коэффициенты квадратного уравнения.

если D > 0, то уравнение имеет два корня;

если D = 0, то уравнение имеет одно решение;
если D < 0, то уравнение не имеет корней.

Пример. Решите уравнение



Следовательно, уравнение имеет два различных корня, найдём их:


Итак,

- корни квадратных уравнений.

Если

Ученики работают в тетрадях.
Каждый выполняет

задание того уровня, который он выбрал.

1 уровень № 434(1), № 434(2).

2 уровень № 440(1), № 440(3)

один вывод формул корней квадратного уравнения.
№434(3,4), №440(5,6).

Постарайтесь найти сведения о золотом (божественном) сечении.

для групп – на карточках.

Решить уравнение:
Решение:



Ответ:

б) Дополнительное задание:

Решение:


Ответ:

Молодцы!!!
Оцените степень сложности урока.
Вам было на уроке:
♦

легко;
♦ обычно;
♦ трудно ?
Оцените степень вашего усвоения материала:
♦ усвоил полностью, могу применить;
♦ усвоил полностью, но затрудняюсь в применении;
♦ усвоил частично;
♦ не усвоил.