Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение заданий №19 (задания на клетчатой бумаге)
Содержание
- 1. Решение заданий №19 (задания на клетчатой бумаге)
- 2. Основные типы задачОпределение тангенса угла;Определение площади фигуры
- 3. При решении задач с использованием клетчатой бумаги
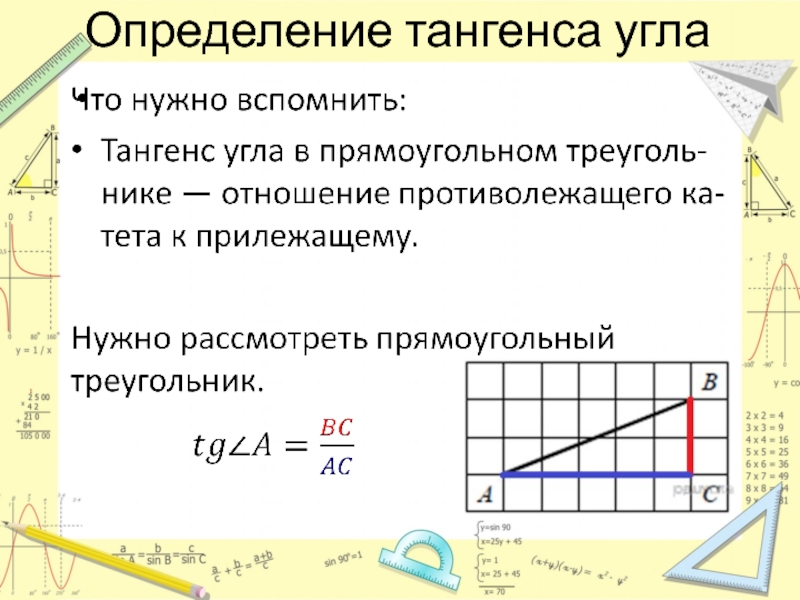
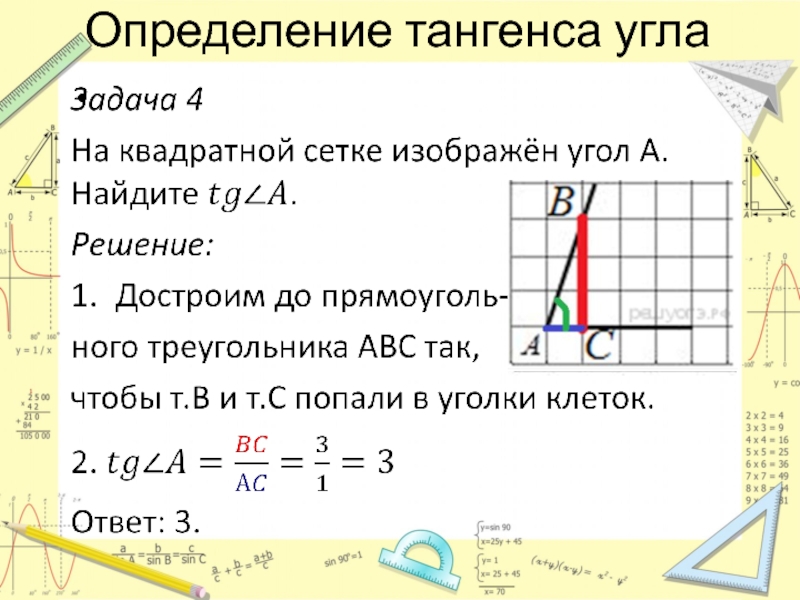
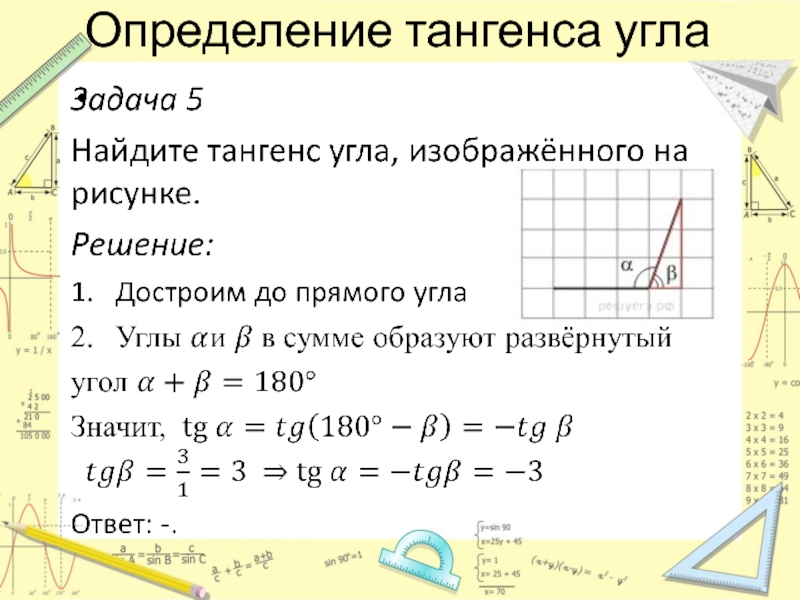
- 4. Определение тангенса угла
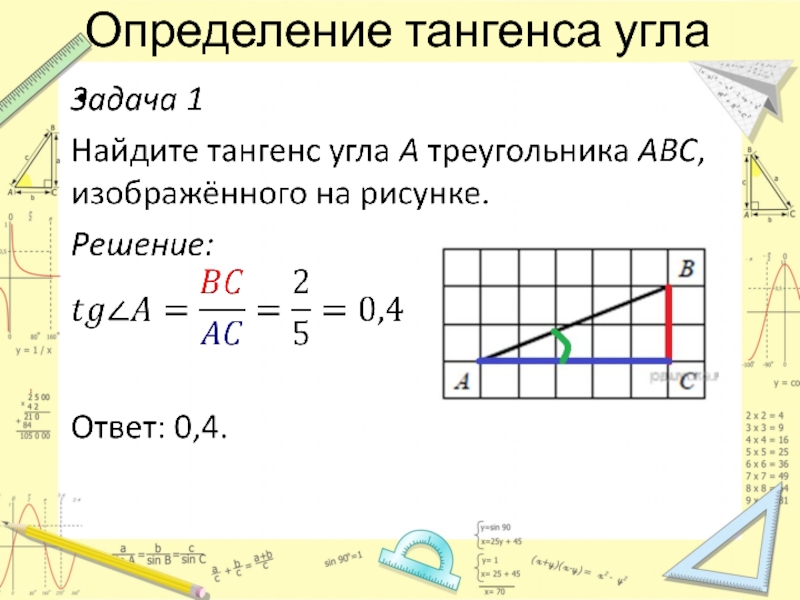
- 5. Определение тангенса угла
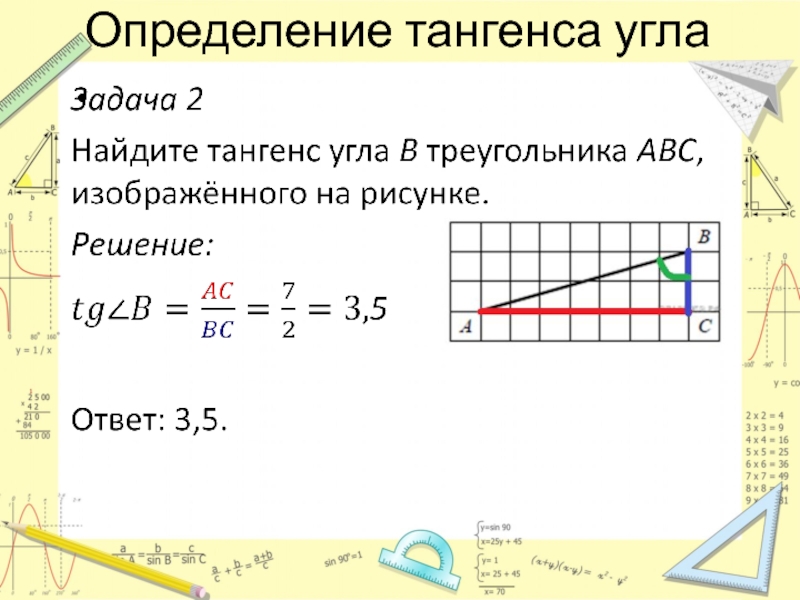
- 6. Определение тангенса угла
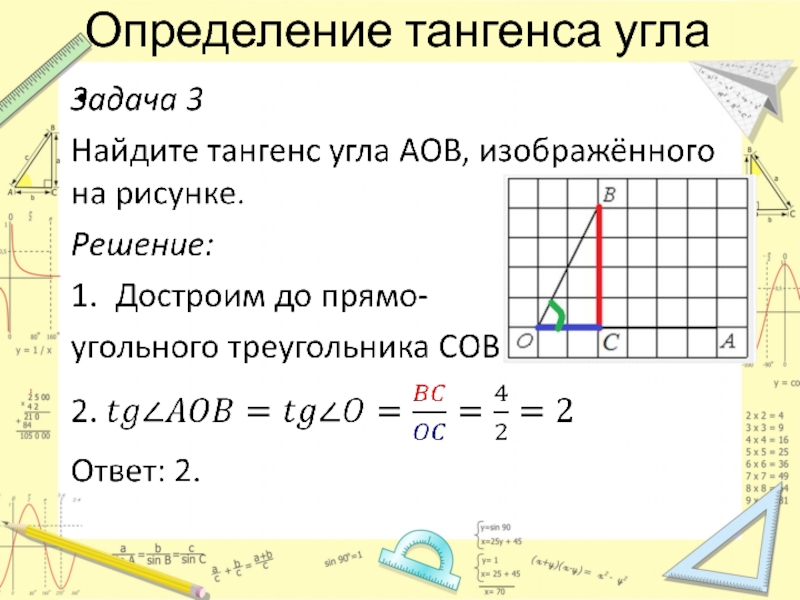
- 7. Определение тангенса угла
- 8. Определение тангенса угла
- 9. Определение тангенса угла
- 10. Определение тангенса угла
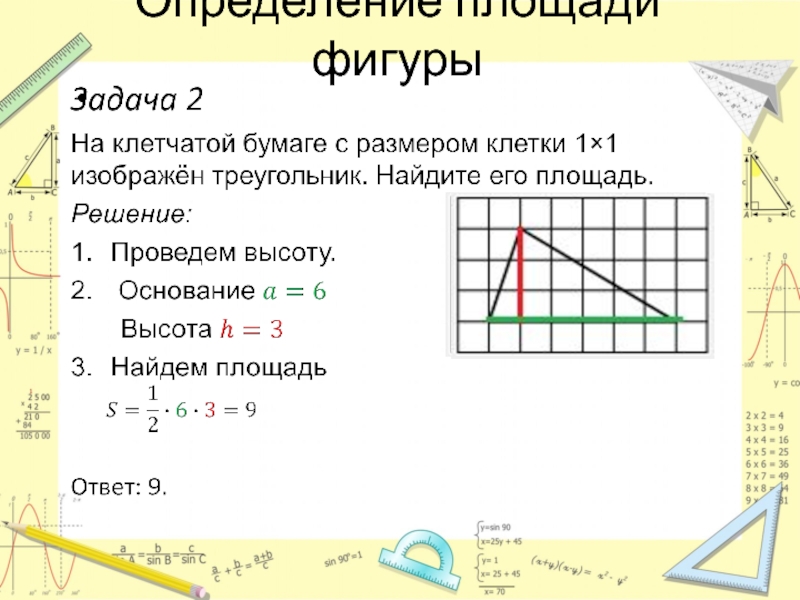
- 11. Определение площади фигуры
- 12. Определение площади фигуры
- 13. Определение площади фигуры
- 14. Определение площади фигуры
- 15. Определение площади фигуры
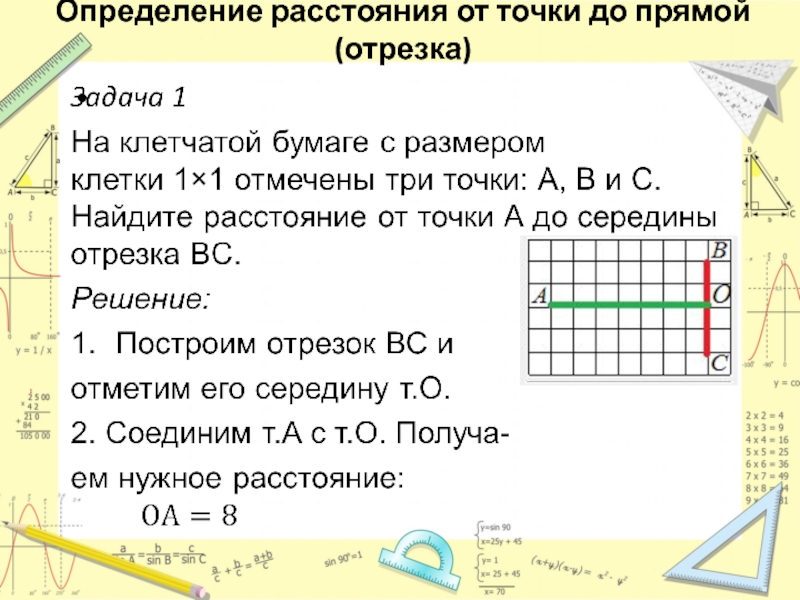
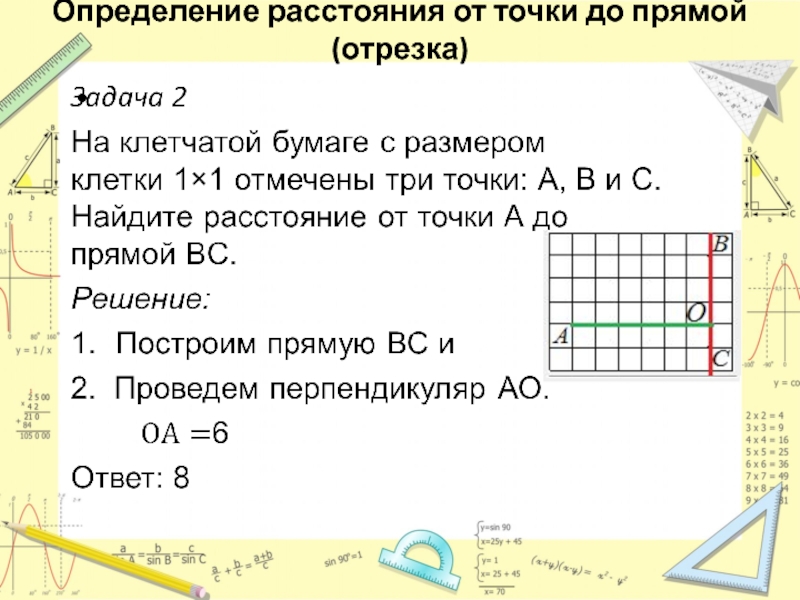
- 16. Определение расстояния от точки до прямой (отрезка)Что
- 17. Определение расстояния от точки до прямой (отрезка)
- 18. Определение расстояния от точки до прямой (отрезка)
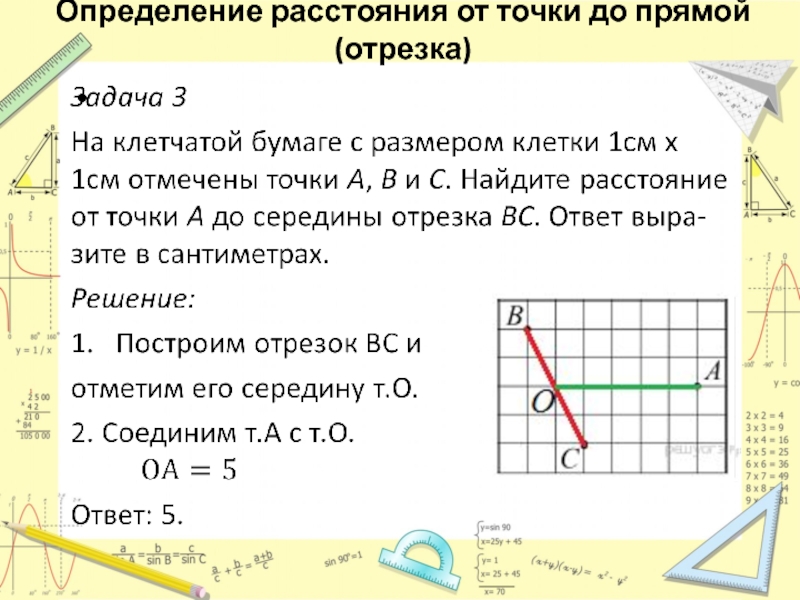
- 19. Определение расстояния от точки до прямой (отрезка)
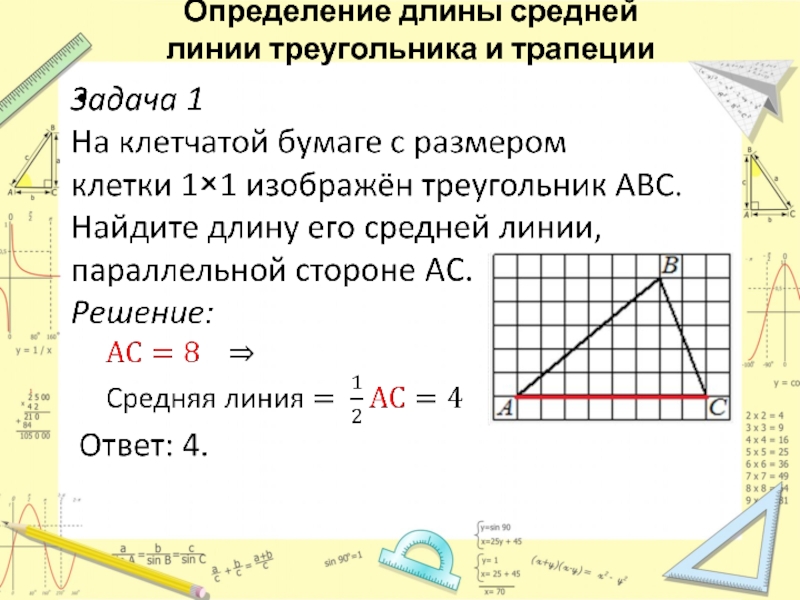
- 20. Определение длины средней линии треугольника и
- 21. Определение длины средней линии треугольника и трапеции
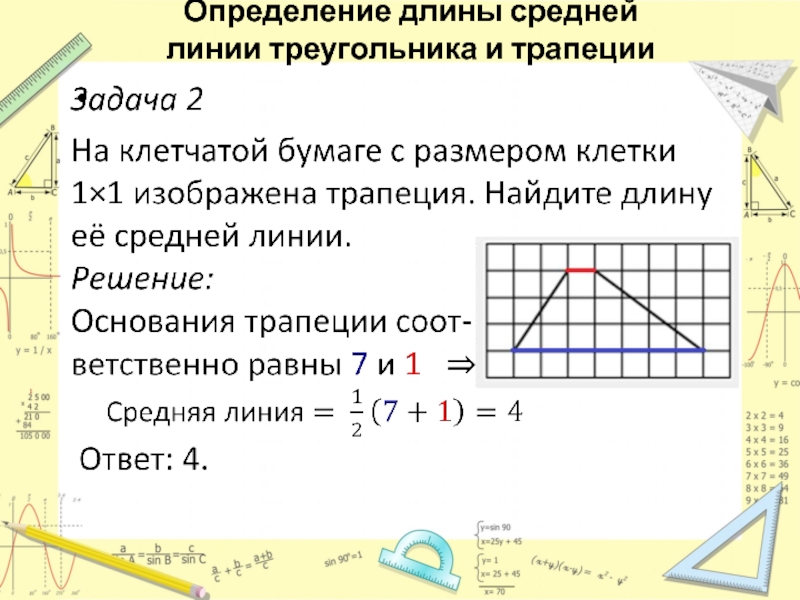
- 22. Определение длины средней линии треугольника и трапеции
- 23. Определение длины большего катета, большей диагоналиЧто нужно
- 24. Задача 1На клетчатой бумаге с размером клетки 1×1 изображён
- 25. Задача 2На клетчатой бумаге с размером клетки
- 26. Определение площади сложных или составных фигур
- 27. Задача 1На клетчатой бумаге с размером клетки
- 28. Определение площади сложных или составных фигур
- 29. Определение градусной меры вписанного углаЧто нужно вспомнить:Вписанный
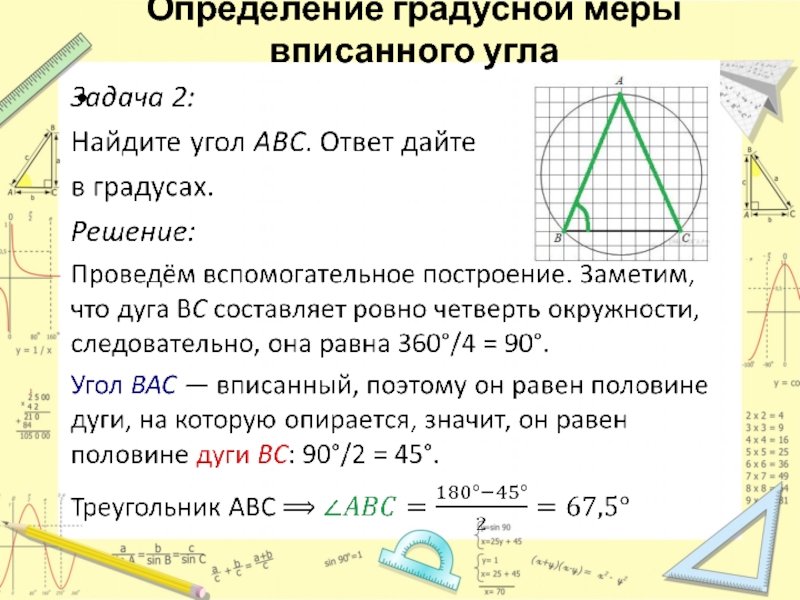
- 30. Задача 1:Найдите угол ABC. Ответ дайте в градусах.Решение:Проведём
- 31. Определение градусной меры вписанного угла
- 32. Определение градусной меры вписанного угла
- 33. Определение градусной меры вписанного угла
- 34. Использованы источники:Открытый банк заданий ОГЭ http://oge.fipi.ruРешу ОГЭ Математика http://oge.sdamgia.ru
- 35. Скачать презентанцию
Основные типы задачОпределение тангенса угла;Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);Определение расстояния от точки до прямой (отрезка);Определение длины средней линии треугольника и трапеции;Определение длины большего катета, большей диагонали;Определение площади сложных или
Слайды и текст этой презентации
Слайд 1Решение заданий №19
(задания на клетчатой бумаге)
Разработано учителем математики
МБОУ «СОШ
№16»
Слайд 2Основные типы задач
Определение тангенса угла;
Определение площади фигуры (ромба, трапеции, параллелограмма,
треугольника);
Определение расстояния от точки до прямой (отрезка);
Определение длины средней линии
треугольника и трапеции;Определение длины большего катета, большей диагонали;
Определение площади сложных или составных фигур;
Определение градусной меры вписанного угла.
Слайд 3При решении задач с использованием клетчатой бумаги важно помнить, что
«клеточки» должны помогать! А значит, нужно подумать как они могут
помочь.По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.
Слайд 16Определение расстояния от точки до прямой (отрезка)
Что нужно вспомнить:
Расстояние от
точки до прямой равно перпендикуляру, опущенному из этой точки на
прямую.
Слайд 20Определение длины средней
линии треугольника и трапеции
Что нужно вспомнить:
Средняя линия
треугольника параллельна третей стороне и равна её половине;
Средняя линия трапеции
равна полусумме оснований. 
Слайд 23Определение длины большего катета, большей диагонали
Что нужно вспомнить:
Стороны прямоугольного треугольника:
катеты – образуют прямой угол:
гипотенуза – лежит напротив прямого угла.
Диагональ
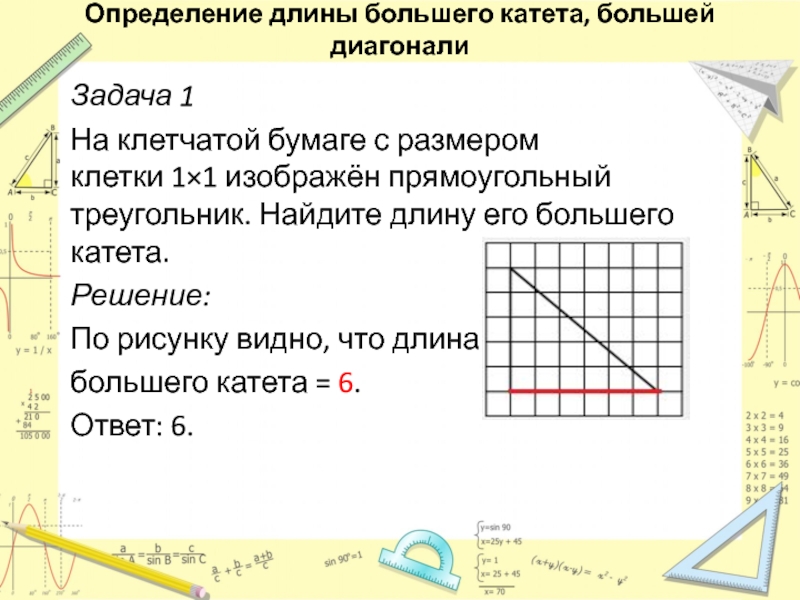
– отрезок соединяющий две не соседние вершины.
Слайд 24Задача 1
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите
длину его большего катета.
Решение:
По рисунку видно, что длина
большего
катета = 6.Ответ: 6.
Определение длины большего катета, большей диагонали
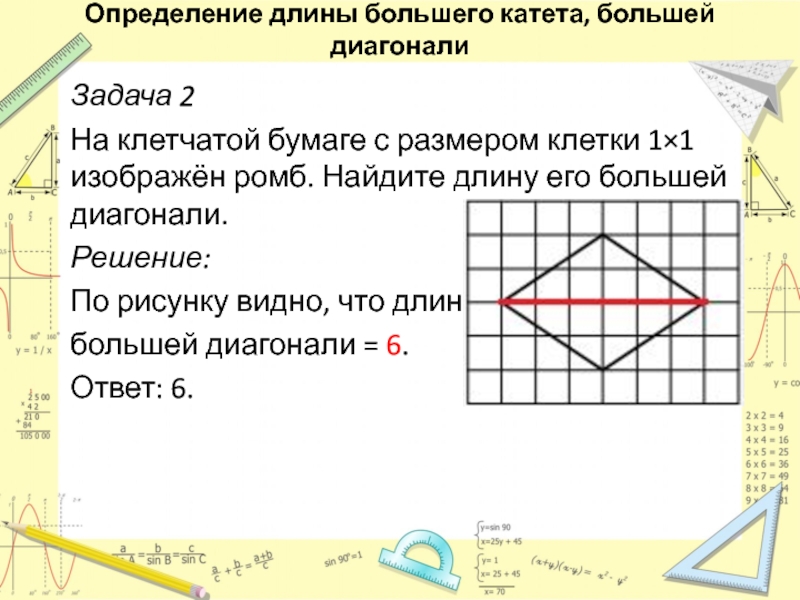
Слайд 25Задача 2
На клетчатой бумаге с размером клетки 1×1 изображён ромб.
Найдите длину его большей диагонали.
Решение:
По рисунку видно, что длина
большей
диагонали = 6.Ответ: 6.
Определение длины большего катета, большей диагонали
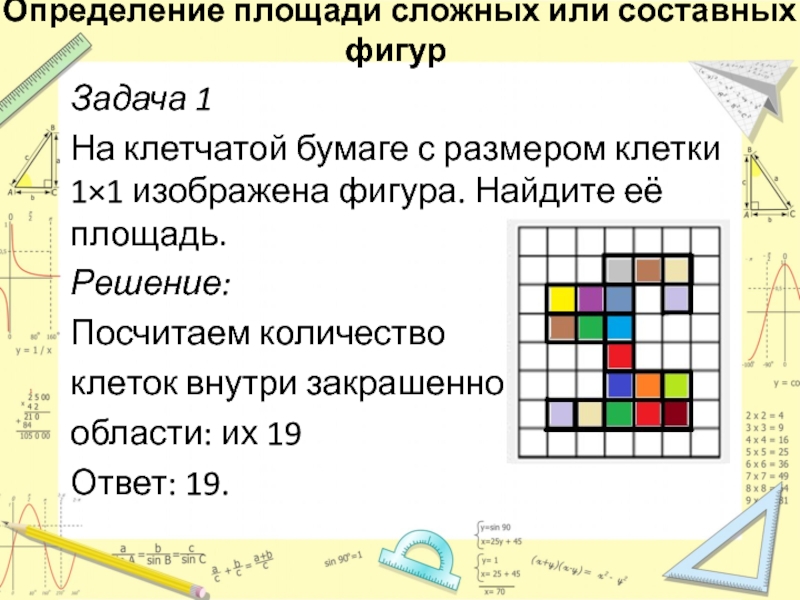
Слайд 27Задача 1
На клетчатой бумаге с размером клетки 1×1 изображена фигура.
Найдите её площадь.
Решение:
Посчитаем количество
клеток внутри закрашенной
области: их 19
Ответ:
19.Определение площади сложных или составных фигур
Слайд 29Определение градусной меры вписанного угла
Что нужно вспомнить:
Вписанный угол – угол,
вершина которого лежит на окружности, а стороны её пересекают.
Центральный угол
– угол, вершина которого совпадает с центром окружности, а стороны её пересекают.Вписанный угол равен половине дуги, на которую опирается.
Слайд 30Задача 1:
Найдите угол ABC. Ответ дайте
в градусах.
Решение:
Проведём вспомогательное построение. Заметим,
что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.
Угол ABC —
вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°.Ответ: 45.
Определение градусной меры вписанного угла
Слайд 34Использованы источники:
Открытый банк заданий ОГЭ http://oge.fipi.ru
Решу ОГЭ Математика http://oge.sdamgia.ru
