Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение заданий С2 ЕГЭ по математике координатно-векторным методом
Содержание
- 1. Решение заданий С2 ЕГЭ по математике координатно-векторным методом
- 2. СОДЕРЖАНИЕ1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В СИСТЕМЕ КООРДИНАТ2. ТИПЫ ЗАДАЧ И МЕТОДЫ ИХ РЕШЕНИЯ3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 3. Слайд 3
- 4. Слайд 4
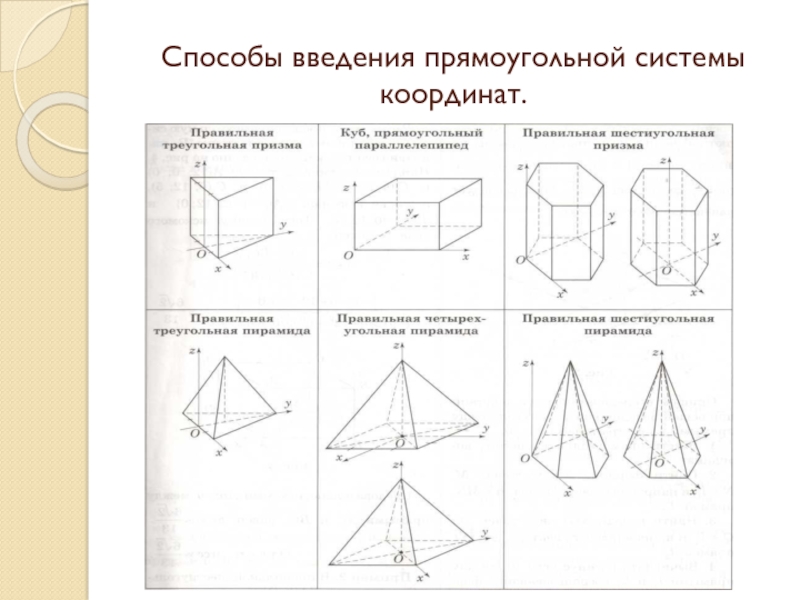
- 5. Способы введения прямоугольной системы координат.
- 6. Способы решения заданий С2
- 7. Слайд 7
- 8. Слайд 8
- 9. Тип 4. Расстояние от точки до прямой.
- 10. Слайд 10
- 11. Слайд 11
- 12. Задача 1. В правильной треугольной пирамиде
- 13. Задача 1. В правильной треугольной пирамиде
- 14. Задача 1. В правильной треугольной пирамиде
- 15. Задача 1. В правильной треугольной пирамиде
- 16. Задача 1. В правильной треугольной пирамиде
- 17. Задача 1. В правильной треугольной пирамиде
- 18. Задача 2. В прямой четырехугольной призме
- 19. Задача 2. В прямой четырехугольной призме
- 20. Задача 2. В прямой четырехугольной призме
- 21. Задача 2. В прямой четырехугольной призме
- 22. Задача 2. В прямой четырехугольной призме
- 23. Задача 2. В прямой четырехугольной призме
- 24. Задача 3. Основание прямой четырехугольной призмы
- 25. Задача 3. Основание прямой четырехугольной призмы
- 26. Задача 3. Основание прямой четырехугольной призмы
- 27. Задача 3. Основание прямой четырехугольной призмы
- 28. Задача 3. Основание прямой четырехугольной призмы
- 29. Задача 4. В правильной четырехугольной призме
- 30. Задача 4. В правильной четырехугольной призме
- 31. Задача 4. В правильной четырехугольной призме
- 32. Задача 4. В правильной четырехугольной призме
- 33. Задача 4. В правильной четырехугольной призме
- 34. Задача 4. В правильной четырехугольной призме
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Решение заданий С2 ЕГЭ по математике
координатно-векторным методом
Выполнила: учитель математики
Заруцкая Н.В.
Слайд 2СОДЕРЖАНИЕ
1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В СИСТЕМЕ КООРДИНАТ
2. ТИПЫ ЗАДАЧ И МЕТОДЫ
ИХ РЕШЕНИЯ
3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Слайд 3
Преимущества метода: -
позволяет решать любые задачи на нахождение углов и расстояний в многогранниках без построения сечений; - основной материал изучался совсем недавно – в 11-ом классе; - рассмотрение геометрических соотношений заменяется алгебраическими действиями.Слайд 4
Что нужно: - повторить материал по учебнику 11-го класса; - показать удобные способы введения прямоугольной системы координат для различных многогранников; - научить определять координаты нормального вектора плоскости; - рассмотреть с учащимися последовательность (можно раздать учащимся памятки) действий при решении задач каждого вида;
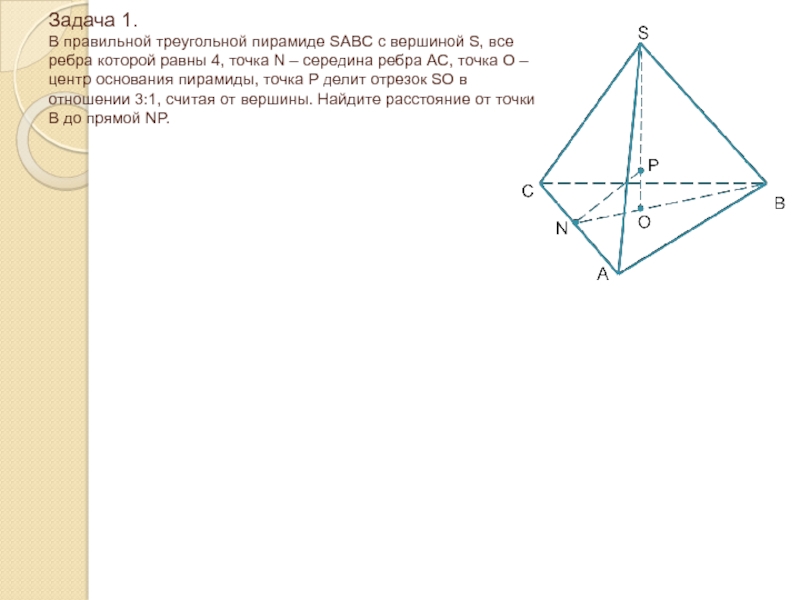
Слайд 12Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.Слайд 13Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
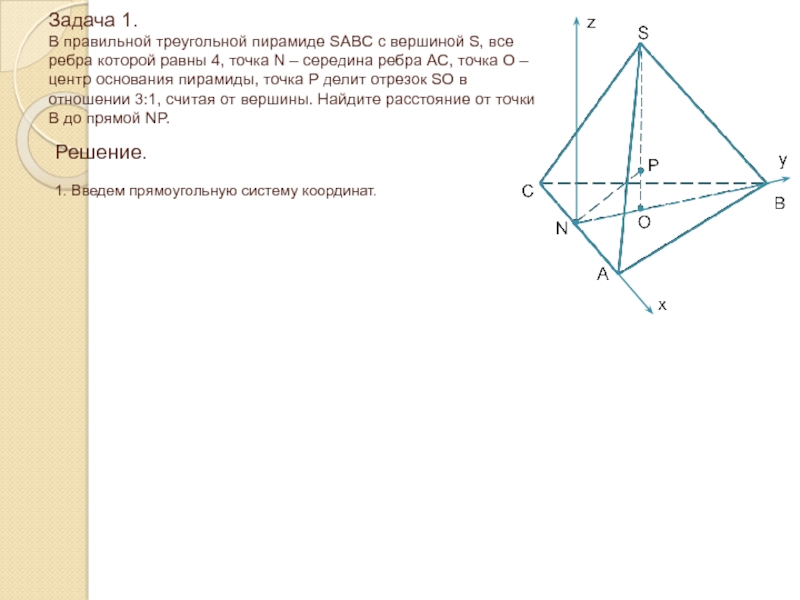
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.Решение.
1. Введем прямоугольную систему координат.
Слайд 14Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.Слайд 15Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.Слайд 16Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.Слайд 17Задача 1. В правильной треугольной пирамиде SABC с вершиной S,
все ребра которой равны 4, точка N – середина ребра
AC, точка O – центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины. Найдите расстояние от точки B до прямой NP.О т в е т: 2.
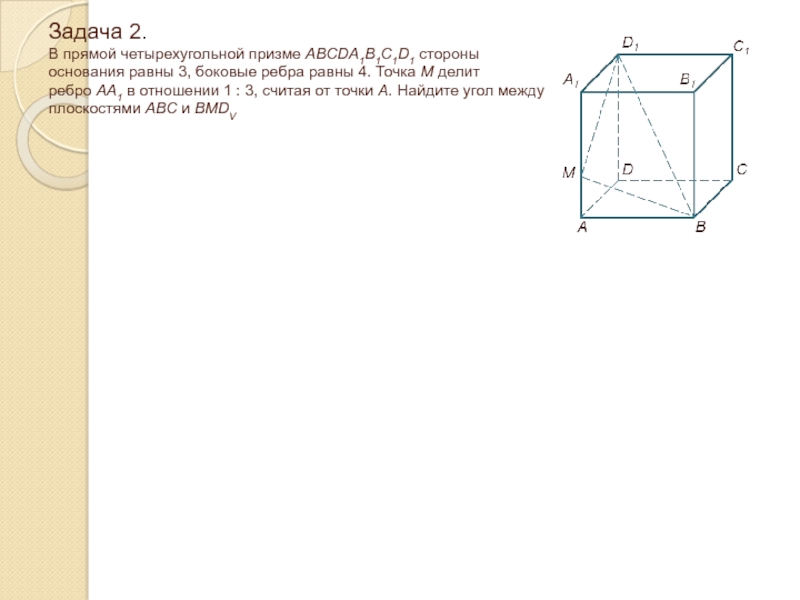
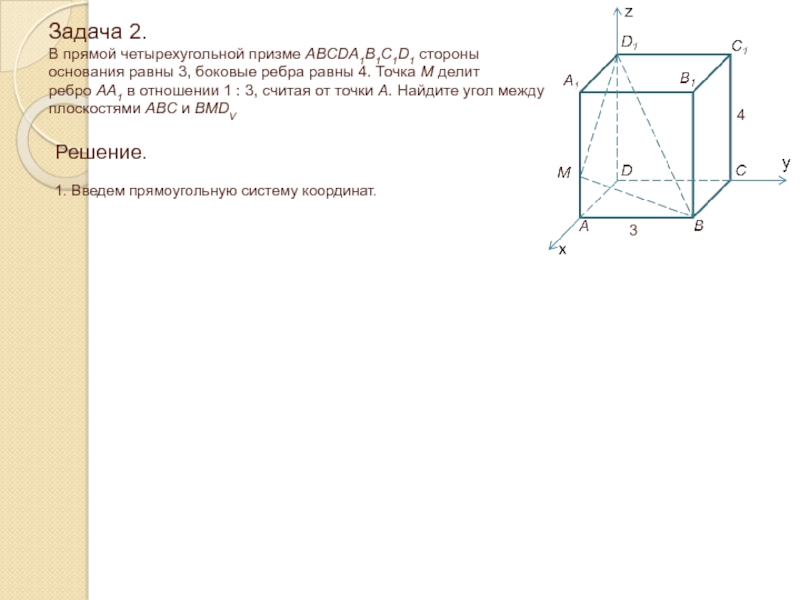
Слайд 18Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVСлайд 19Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVРешение.
1. Введем прямоугольную систему координат.
3
4
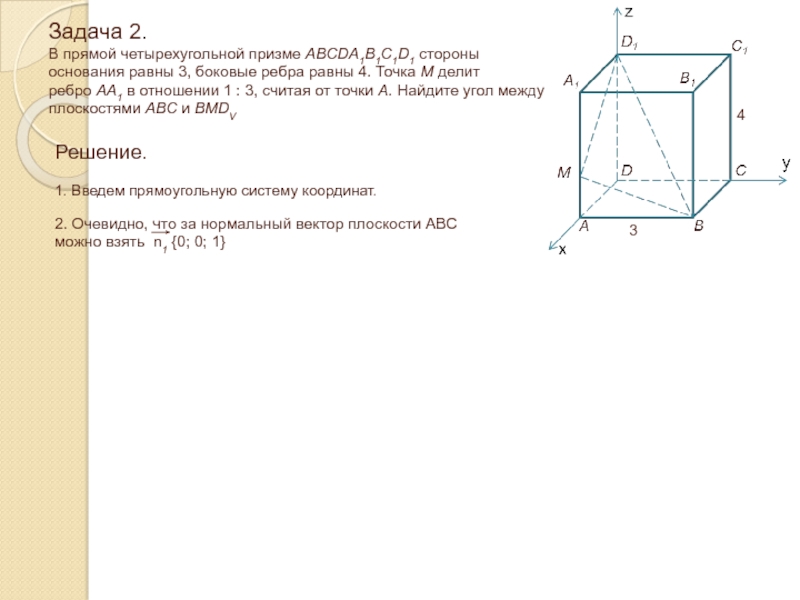
Слайд 20Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVРешение.
1. Введем прямоугольную систему координат.
3
4
2. Очевидно, что за нормальный вектор плоскости ABC можно взять n1 {0; 0; 1}
Слайд 21Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVРешение.
1. Введем прямоугольную систему координат.
3
4
2. Очевидно, что за нормальный вектор плоскости ABC можно взять n1 {0; 0; 1}
3. Определим координаты 3-х точек плоскости BMD1 не лежащих на одной прямой:
B (3; 3; 0) M (3; 0; 1) D1 (0; 0; 4)
и координаты векторов: BM {0; 3; -1} D1M {-3; 0; 3}
Слайд 22Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVРешение.
1. Введем прямоугольную систему координат.
3
4
2. Очевидно, что за нормальный вектор плоскости ABC можно взять n1 {0; 0; 1}
3. Определим координаты 3-х точек плоскости BMD1 не лежащих на одной прямой:
B (3; 3; 0) M (3; 0; 1) D1 (0; 0; 4)
и координаты векторов: BM {0; 3; -1} D1M {-3; 0; 3}
4. Найдем неизвестные координаты {a; b; c} нормального вектора n2 плоскости BMD1 из условия
n2 · BM = 0, 0 · a + 3 · b + (-1) · c = 0, 3b – c = 0,
n2 · D1M = 0; (-3) · a + 0 · b + 3 · c = 0; -3a + 3c = 0;
Выберем b = 1, получим c = 3, a = 3. Вектор n2 {3; 1; 3}
Слайд 23Задача 2. В прямой четырехугольной призме ABCDA1B1C1D1 стороны основания равны
3, боковые ребра равны 4. Точка М делит ребро АА1
в отношении 1 : 3, считая от точки А. Найдите угол между плоскостями ABC и BMDVРешение.
1. Введем прямоугольную систему координат.
3
4
2. Очевидно, что за нормальный вектор плоскости ABC можно взять n1 {0; 0; 1}
3. Определим координаты 3-х точек плоскости BMD1 не лежащих на одной прямой:
B (3; 3; 0) M (3; 0; 1) D1 (0; 0; 4)
и координаты векторов: BM {0; 3; -1} D1M {-3; 0; 3}
4. Найдем неизвестные координаты {a; b; c} нормального вектора n2 плоскости BMD1 из условия
n2 · BM = 0, 0 · a + 3 · b + (-1) · c = 0, 3b – c = 0,
n2 · D1M = 0; (-3) · a + 0 · b + 3 · c = 0; -3a + 3c = 0;
Выберем b = 1, получим c = 3, a = 3. Вектор n2 {3; 1; 3}
5. Найдем косинус угла θ между плоскостями:
О т в е т:
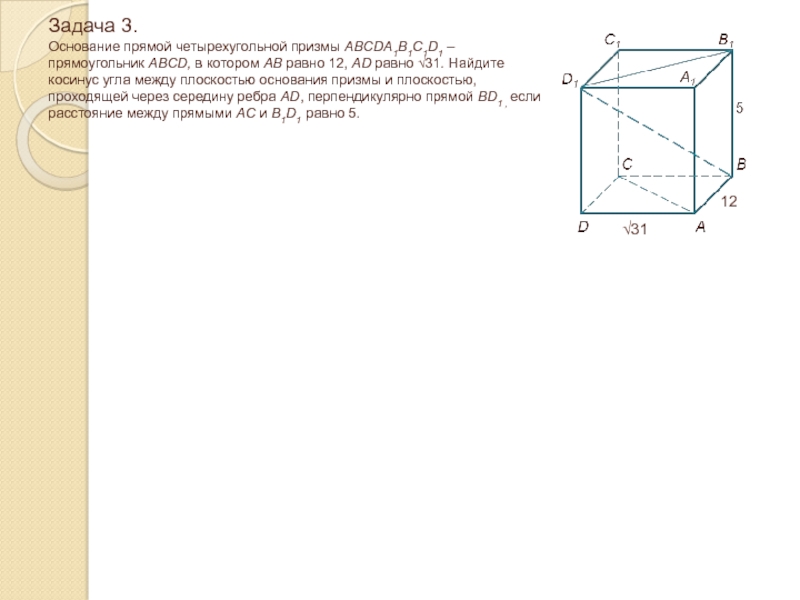
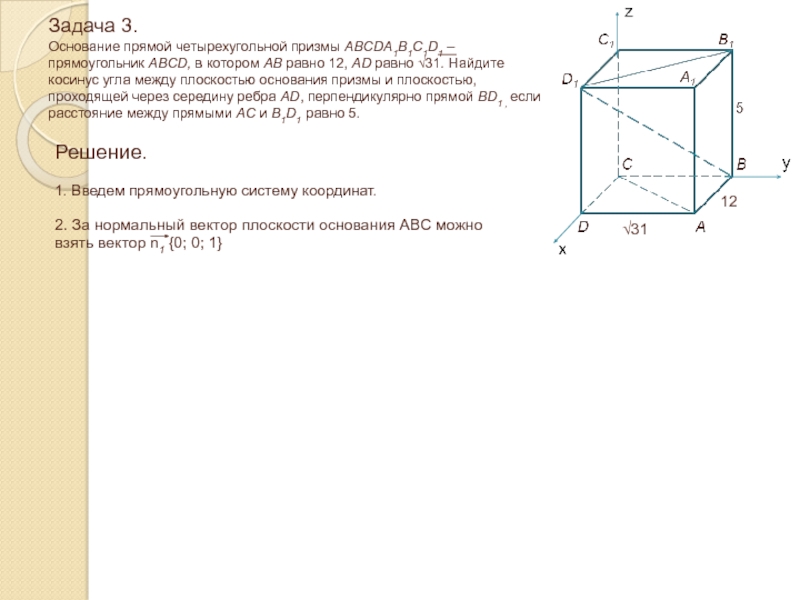
Слайд 24Задача 3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD,
в котором AB равно 12, AD равно √31. Найдите косинус
угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD, перпендикулярно прямой BD1 , если расстояние между прямыми AC и B1D1 равно 5.√31
12
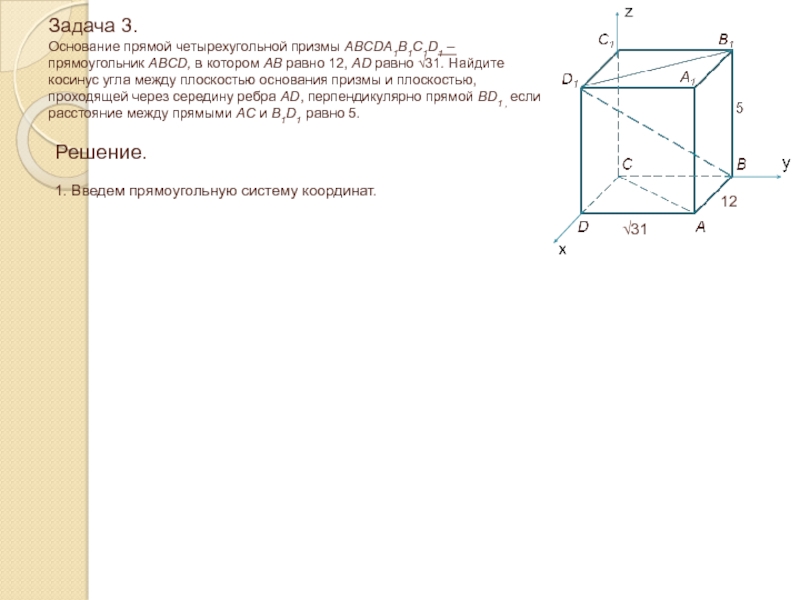
Слайд 25Задача 3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD,
в котором AB равно 12, AD равно √31. Найдите косинус
угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD, перпендикулярно прямой BD1 , если расстояние между прямыми AC и B1D1 равно 5.Решение.
1. Введем прямоугольную систему координат.
√31
12
Слайд 26Задача 3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD,
в котором AB равно 12, AD равно √31. Найдите косинус
угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD, перпендикулярно прямой BD1 , если расстояние между прямыми AC и B1D1 равно 5.Решение.
1. Введем прямоугольную систему координат.
2. За нормальный вектор плоскости основания ABC можно взять вектор n1 {0; 0; 1}
√31
12
Слайд 27Задача 3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD,
в котором AB равно 12, AD равно √31. Найдите косинус
угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD, перпендикулярно прямой BD1 , если расстояние между прямыми AC и B1D1 равно 5.Решение.
1. Введем прямоугольную систему координат.
2. За нормальный вектор плоскости основания ABC можно взять вектор n1 {0; 0; 1}
3. Нормальным вектором искомой плоскости можно считать вектор n2 =
Найдем его координаты.
BD1 ,
B (0; √31; 0) D1 (12; 0; 5) BD1 {12; -√31; 5}
12
Слайд 28Задача 3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD,
в котором AB равно 12, AD равно √31. Найдите косинус
угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD, перпендикулярно прямой BD1 , если расстояние между прямыми AC и B1D1 равно 5.Решение.
1. Введем прямоугольную систему координат.
2. За нормальный вектор плоскости основания ABC можно взять вектор n1 {0; 0; 1}
3. Нормальным вектором искомой плоскости можно считать вектор n2 =
Найдем его координаты.
BD1 ,
B (0; √31; 0) D1 (12; 0; 5) BD1 {12; -√31; 5}
12
4. Найдем косинус угла θ между плоскостями:
О т в е т:
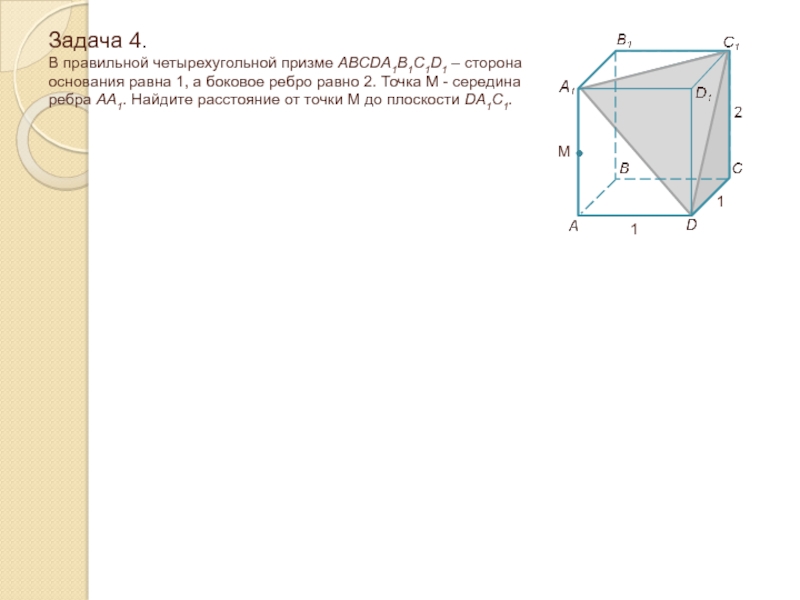
Слайд 29Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
Слайд 30Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
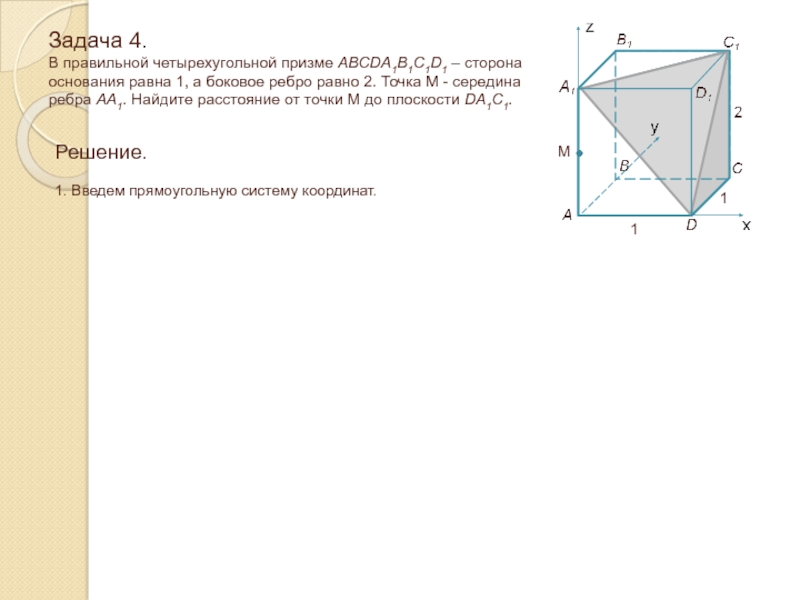
Решение.
1. Введем прямоугольную систему координат.
Слайд 31Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
Решение.
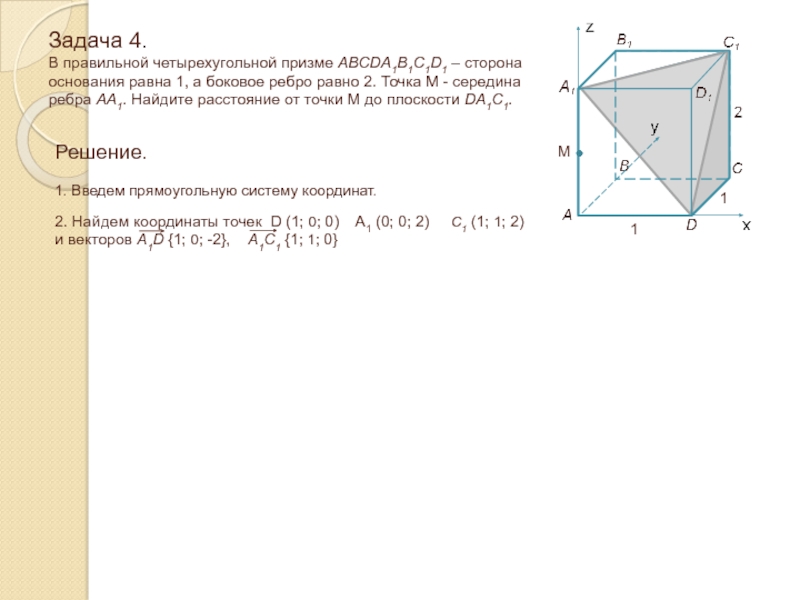
1. Введем прямоугольную систему координат.
2. Найдем координаты точек D (1; 0; 0) A1 (0; 0; 2) C1 (1; 1; 2)
и векторов A1D {1; 0; -2}, A1C1 {1; 1; 0}
Слайд 32Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
Решение.
1. Введем прямоугольную систему координат.
2. Найдем координаты точек D (1; 0; 0) A1 (0; 0; 2) C1 (1; 1; 2)
и векторов A1D {1; 0; -2}, A1C1 {1; 1; 0}.
3. Найдем координаты вектора n {a; b; c} из условия:
n · A1D = 0, 1 · a + 0 · b + (-2) · c = 0, a = 2c,
n · A1C = 0; 1 · a + 1 · b + 0 · c = 0; b = -a;
Пусть c = 1, тогда вектор n {2; -2; 1}
Слайд 33Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
Решение.
1. Введем прямоугольную систему координат.
2. Найдем координаты точек D (1; 0; 0) A1 (0; 0; 2) C1 (1; 1; 2)
и векторов A1D {1; 0; -2}, A1C1 {1; 1; 0}.
3. Найдем координаты вектора n {a; b; c} из условия:
n · A1D = 0, 1 · a + 0 · b + (-2) · c = 0, a = 2c,
n · A1C = 0; 1 · a + 1 · b + 0 · c = 0; b = -a;
Пусть c = 1, тогда вектор n {2; -2; 1}
4. Найдем координаты точки M (0; 0; 1) и вектора MA1 {0; 0; 1}.
Слайд 34Задача 4. В правильной четырехугольной призме ABCDA1B1C1D1 – сторона основания
равна 1, а боковое ребро равно 2. Точка M -
середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.1
1
M
Решение.
1. Введем прямоугольную систему координат.
2. Найдем координаты точек D (1; 0; 0) A1 (0; 0; 2) C1 (1; 1; 2)
и векторов A1D {1; 0; -2}, A1C1 {1; 1; 0}.
3. Найдем координаты вектора n {a; b; c} из условия:
n · A1D = 0, 1 · a + 0 · b + (-2) · c = 0, a = 2c,
n · A1C = 0; 1 · a + 1 · b + 0 · c = 0; b = -a;
Пусть c = 1, тогда вектор n {2; -2; 1}
4. Найдем координаты точки M (0; 0; 1) и вектора MA1 {0; 0; 1}.
О т в е т: