Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синус, косинус, тангенс, котангенс угла
Содержание
- 1. Синус, косинус, тангенс, котангенс угла
- 2. Синусом острого угла прямоугольного треугольника называется отношение
- 3. Определение: полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.
- 4. Значения синуса, косинуса и тангенса для углов
- 5. Значения синуса, косинусаТак как координаты (х; у)
- 6. sin = ∆OMD
- 7. Основное тригонометрическое тождествох2 + у2 = 1
- 8. Найдите cosα:
- 9. Найдите sinα:
- 10. Формулы приведенияпри 0 ≤ ≤ 90sin
- 11. 11
- 12. 11Как запомнить таблицу?
- 13. 111231
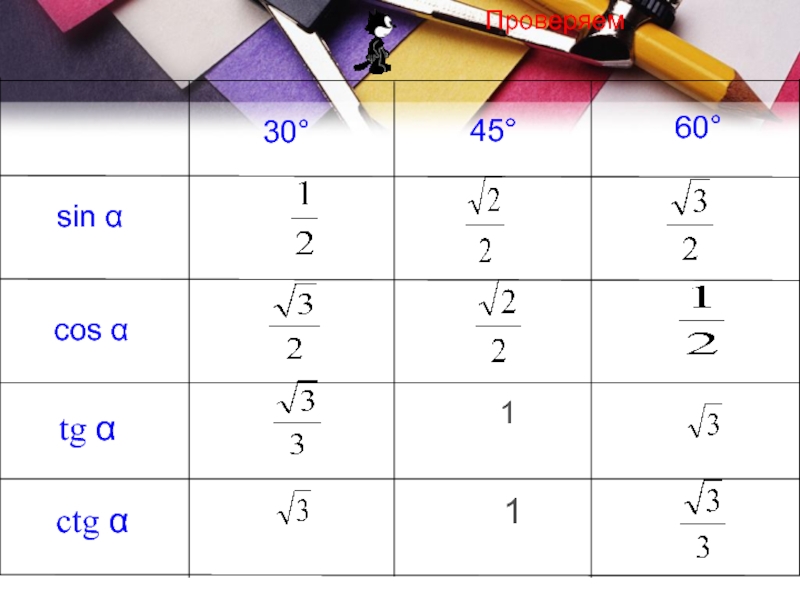
- 14. 11Проверяем
- 15. A (x; y)xyOM (cos α; sin α)Формулы
- 16. Тригонометрия на ладони
- 17. СПАСИБО ЗА ВНИМАНИЕ!
- 18. Скачать презентанцию
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.Тангенсом
Слайды и текст этой презентации
Слайд 2Синусом острого угла прямоугольного треугольника называется отношение противолежащего
катета к
гипотенузе.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего
катета к
гипотенузе.Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Слайд 3Определение: полуокружность называется единичной, если ее центр находится в начале
координат, а радиус равен 1.
Слайд 4Значения синуса, косинуса и тангенса для углов 00, 900 и
1800
Так как точки А, С и B имеют координаты
А
(1; 0), С (0; 1), В (-1; 0), то 
Слайд 5Значения синуса, косинуса
Так как координаты (х; у) заключены в промежутках
0
≤ у ≤ 1, - 1 ≤ х ≤ 1,
то для любого из промежутка0 ≤ ≤ 180
справедливы неравенства:
0 ≤ sin ≤ 1,
- 1≤ cos ≤ 1
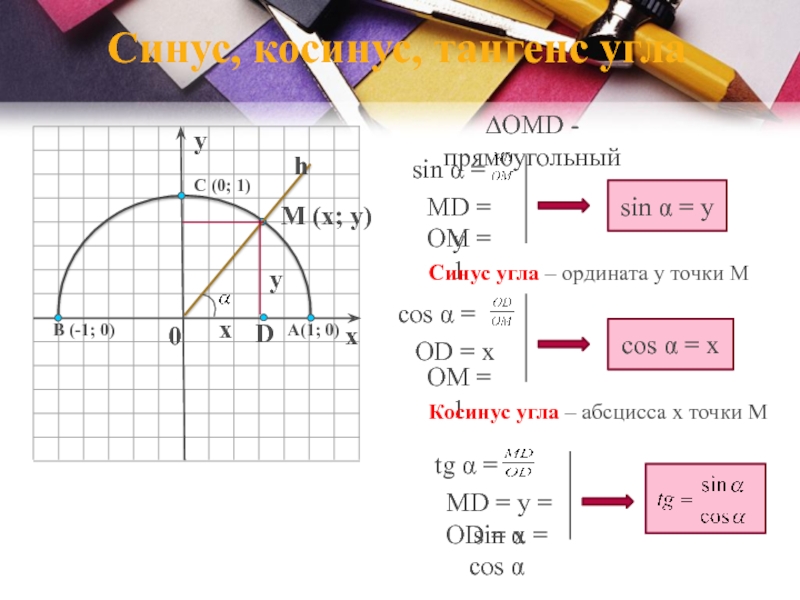
Слайд 6sin =
∆OMD - прямоугольный
MD =
y
OM = 1
sin = y
Синус угла – ордината у
точки Мcos =
OD = x
OM = 1
cos = x
Косинус угла – абсцисса х точки М
Синус, косинус, тангенс угла
tg =
MD = y = sin
OD = x = cos
Слайд 7Основное тригонометрическое тождество
х2 + у2 = 1 - уравнение окружности
sin
= y,
cos = x
sin2α + cos2α = 1
для
любого из промежутка 0 ≤ ≤ 180 
Слайд 10Формулы приведения
при 0 ≤ ≤ 90
sin (90 - )
= cos
cos (90 - ) = sin
sin (180
- )= sin cos (180 - ) = - cos
при 0 ≤ ≤ 180
Слайд 15A (x; y)
x
y
O
M (cos α; sin α)
Формулы для вычисления координат
точки
А (x; y) – произвольная точка
М (сos α; sin α)
x = ОА ∙ cos
y = OA ∙ sin
Слайд 16
Тригонометрия на ладони
мизинец № О
— соответствует 0°; безымянный № 1 — соответствует
30°; средний №2 — соответствует 45°; указательный № 3 — соответствует 60°; большой № 4 — соответствует 90°.
