Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы преобразования графиков функций 10 класс
Содержание
- 1. Способы преобразования графиков функций 10 класс
- 2. IIII-422-1xyБудем обозначать через (х';у') координаты точки, в которую переходит произвольная точка (х;у) плоскости при данном преобразовании.0
- 3. 1) Параллельный перенос вдоль оси ординат на
- 4. 2) Растяжение вдоль оси ординат с коэффициентом
- 5. 3) Параллельный перенос вдоль оси абсцисс на
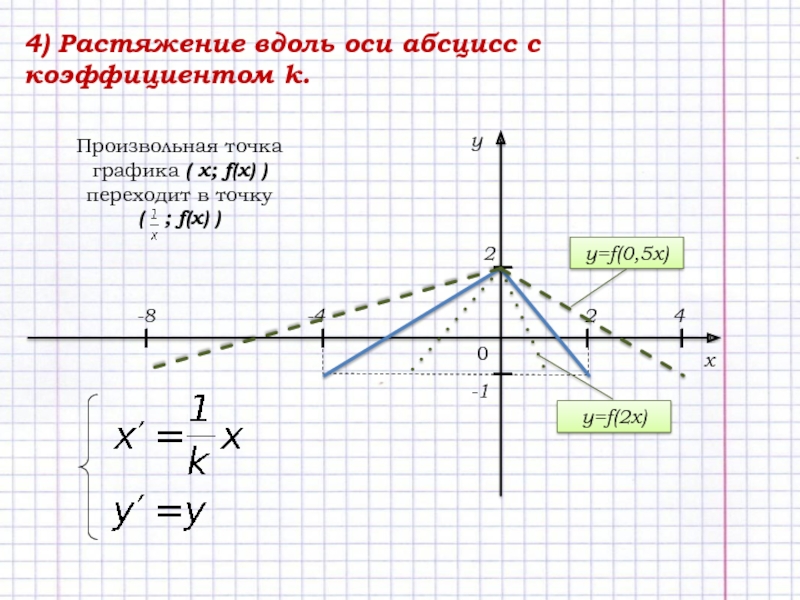
- 6. 4) Растяжение вдоль оси абсцисс с коэффициентом
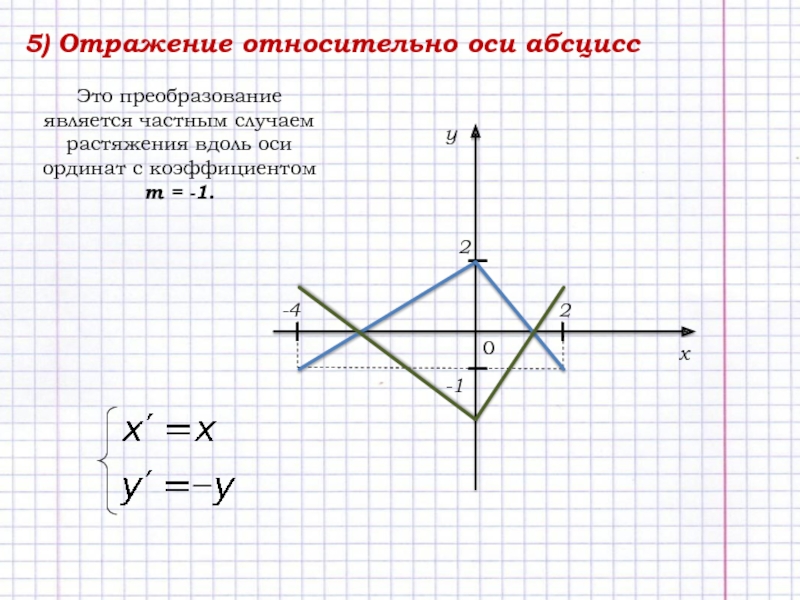
- 7. 5) Отражение относительно оси абсциссЭто преобразование является
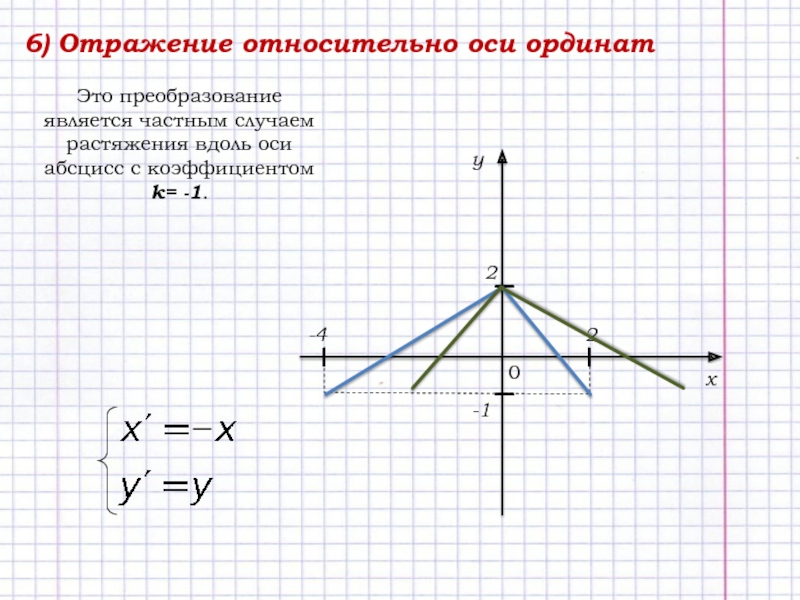
- 8. 6) Отражение относительно оси ординатЭто преобразование является
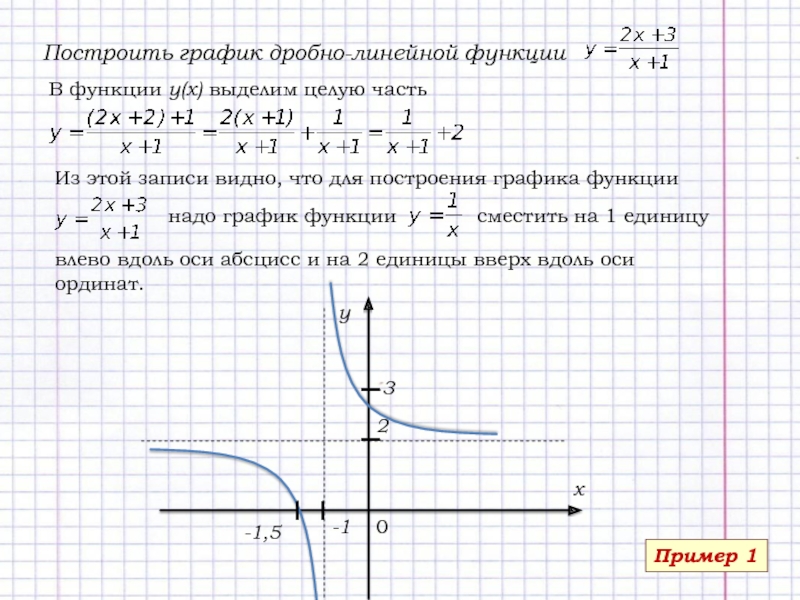
- 9. Построить график дробно-линейной функцииВ функции у(х) выделим
- 10. Пример 2Построим график функции у = 3
- 11. Используя приведённый график функции у = f(x),
- 12. у = f(x)IIIIII0-13-2
- 13. Скачать презентанцию
IIII-422-1xyБудем обозначать через (х';у') координаты точки, в которую переходит произвольная точка (х;у) плоскости при данном преобразовании.0
Слайды и текст этой презентации
Слайд 1Способы преобразования
графиков
Коломина Наталья Николаевна
учитель математики
МКОУ «Хотьковская СОШ»
Думиничского района
Калужской
области
Слайд 2I
I
I
I
-4
2
2
-1
x
y
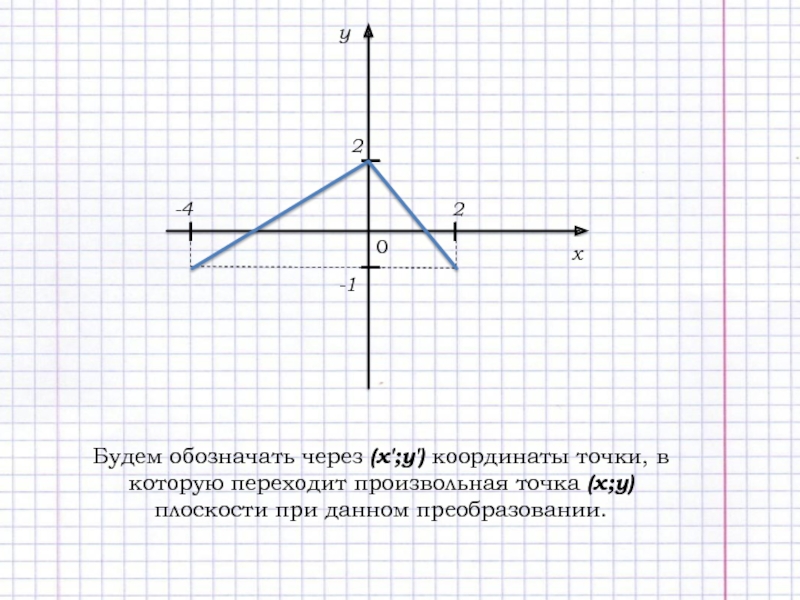
Будем обозначать через (х';у') координаты точки, в которую переходит произвольная
точка (х;у) плоскости при данном преобразовании.
0
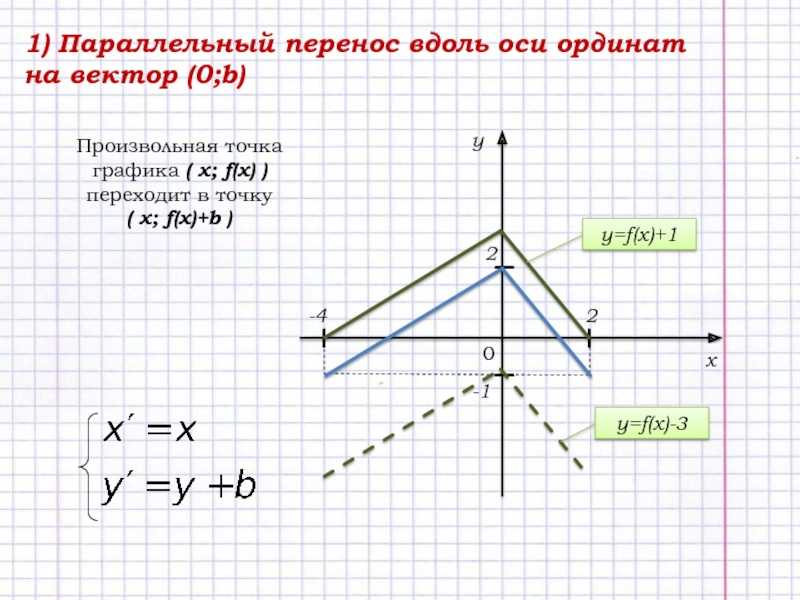
Слайд 31) Параллельный перенос вдоль оси ординат на вектор (0;b)
I
I
I
I
-4
2
2
-1
x
y
Произвольная точка
графика ( х; f(x) )
переходит в точку
( х;
f(x)+b ) y=f(x)+1
y=f(x)-3
0
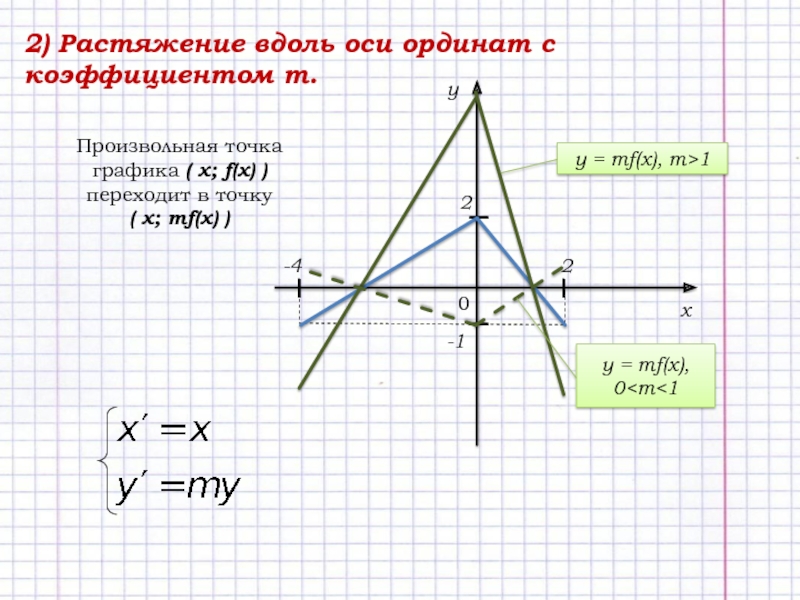
Слайд 42) Растяжение вдоль оси ординат с коэффициентом m.
I
I
I
I
-4
2
2
-1
x
y
Произвольная точка графика
( х; f(x) )
переходит в точку
( х; mf(x)
) y = mf(x), m>1
y = mf(x), 0
0
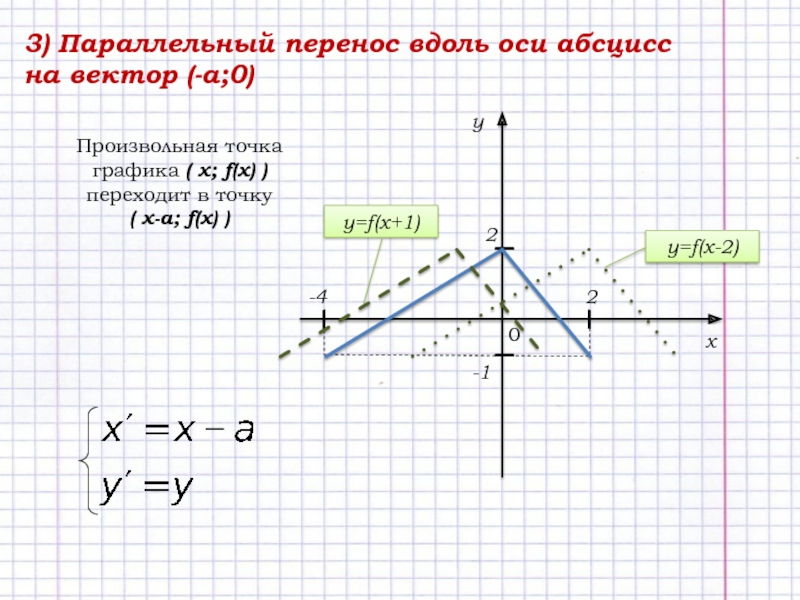
Слайд 53) Параллельный перенос вдоль оси абсцисс на вектор (-a;0)
_
Произвольная точка
графика ( х; f(x) )
переходит в точку
( х-а;
f(x) ) I
I
I
I
-4
2
2
-1
x
y
y=f(x-2)
y=f(x+1)
0
Слайд 64) Растяжение вдоль оси абсцисс с коэффициентом k.
Произвольная точка графика
( х; f(x) )
переходит в точку
( ;
f(x) ) I
I
I
I
-4
2
2
-1
x
y
I
-8
I
4
y=f(2x)
y=f(0,5x)
0
Слайд 75) Отражение относительно оси абсцисс
Это преобразование является частным случаем растяжения
вдоль оси ординат с коэффициентом m = -1.
_
I
I
I
I
-4
2
2
-1
x
y
0
Слайд 86) Отражение относительно оси ординат
Это преобразование является частным случаем растяжения
вдоль оси абсцисс с коэффициентом k= -1.
I
I
I
I
-4
2
2
-1
x
y
_
0
Слайд 9Построить график дробно-линейной функции
В функции у(х) выделим целую часть
Из этой
записи видно, что для построения графика функции
надо график функции
сместить на
1 единицувлево вдоль оси абсцисс и на 2 единицы вверх вдоль оси ординат.
I
I
I
3
2
-1,5
-1
x
y
I
0
Пример 1
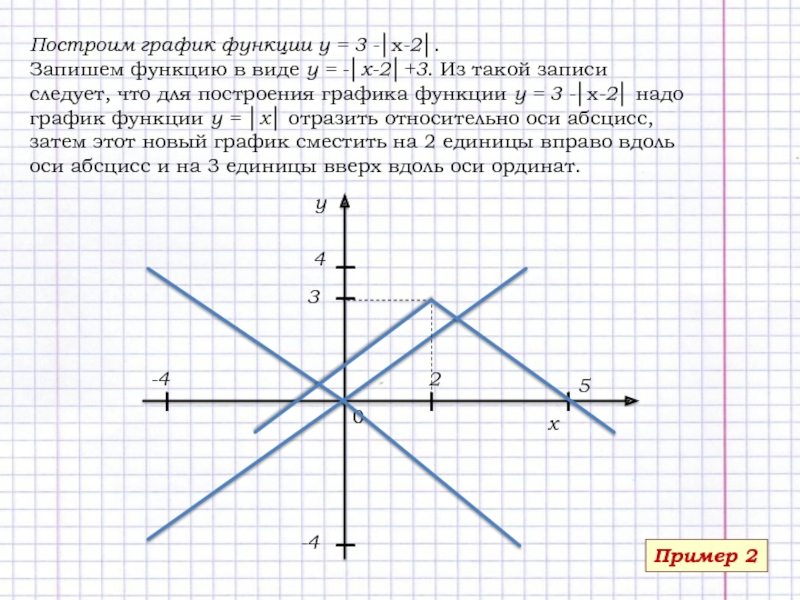
Слайд 10Пример 2
Построим график функции у = 3 -│х-2│.
Запишем функцию
в виде у = -│х-2│+3. Из такой записи следует, что
для построения графика функции у = 3 -│х-2│ надо график функции у = │х│ отразить относительно оси абсцисс, затем этот новый график сместить на 2 единицы вправо вдоль оси абсцисс и на 3 единицы вверх вдоль оси ординат.I
I
I
I
-4
2
4
-4
x
y
0
3
I
5
I
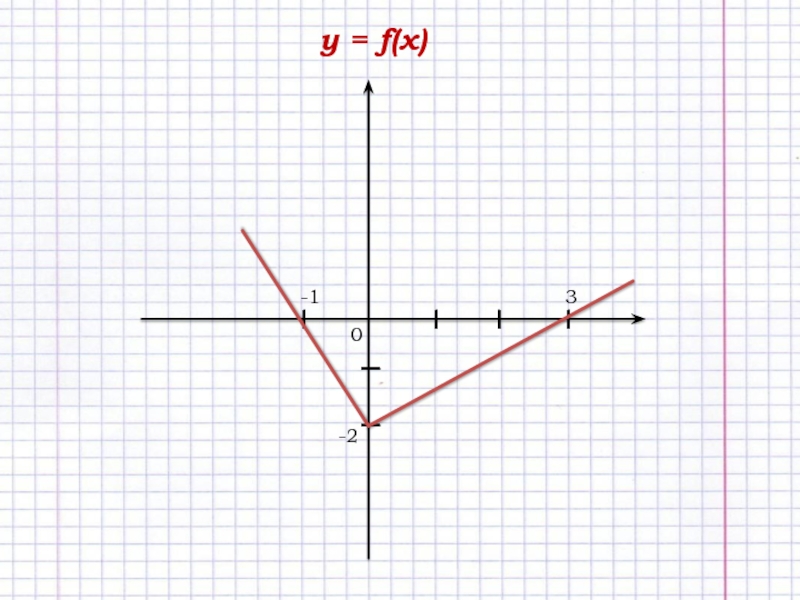
Слайд 11Используя приведённый график функции у = f(x), постройте график функции:
а)
у = f(x)+3;
б) у = f(x)-1;
в) у = 2f(x);
г) у
= 0,5f(x);д) у = f(x+1);
е) у = f(x-2);
ж) у = -f(x);
з) у = f(-x);
и) у = -2f(x);
к) у = f(-0,5x);
л) у = f(-x)+2;
м) у = f(-x+2);
н) у = f(-x)+2;
о) у = 3f(-x)+2
