Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники. Третий признак равенства
Содержание
- 1. Треугольники. Третий признак равенства
- 2. Равенство треугольниковПервый признак равенства треугольников. Если две
- 3. Третий признак равенства треугольниковДано: треугольник
- 4. Достаточно ли равенства указанных элементов, чтобы утверждать,
- 5. Применение третьего признака равенства треугольников к решению
- 6. ПроверкаААВСD – квадрат. Все стороны квадрата равны
- 7. Домашнее задание:Сформулируй третий признак равенства треугольников.Докажи теорему.Повтори решение задач.
- 8. Используемые ресурсы:Сайт школы дистанционного обучения (г.Москва) http://iclass.home-edu.ru/file.php/12/LESSONS/lesson29.htmhttp://dcs.isa.ru/www/vladimirv/Geometry/dshar/sco_3.2.1/sco_3_2_1.htmlУчебник геометрии 7-9
- 9. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Треугольники.
Третий признак равенства
Демонстрационный материал к уроку геометрии в 9
классе
2010Слайд 2Равенство треугольников
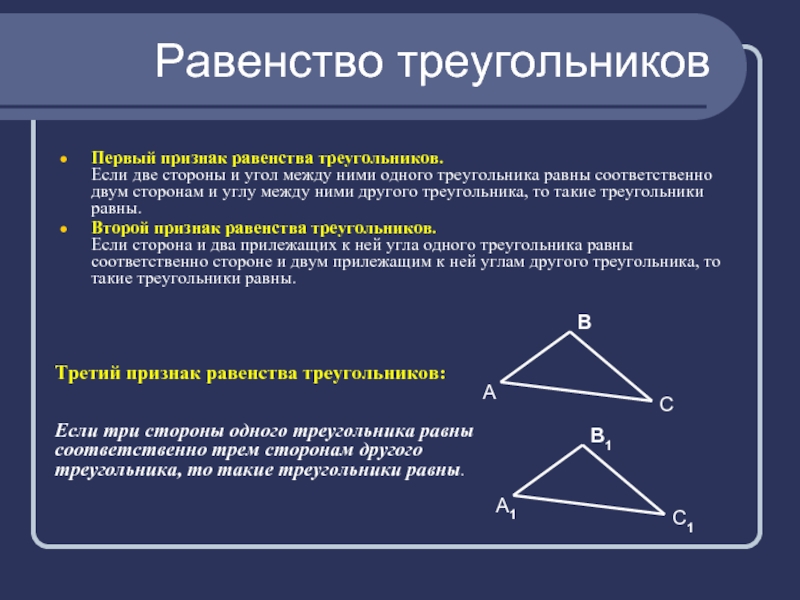
Первый признак равенства треугольников.
Если две стороны и угол между
ними одного треугольника равны соответственно двум сторонам и углу между
ними другого треугольника, то такие треугольники равны.Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников:
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
А
С
В
А1
С1
В1
Слайд 3Третий признак равенства
треугольников
Дано:
треугольник ABC
треугольник A1B1C1
АB=A1B1
BC=B1C1
AC=A1C1
Доказательство
Приложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершины
А совместилась с А1, В с В1, а С и С1 оказались по разные стороны от прямой А1В1. [АС=А1С1 и BC=B1C1 ] => треугольники A1С1С и В1С1С - равнобедренные
[Угол 1 равен углу 2 и угол 3 = углу 4]=> угол A1CB равен углу A1C1B1.
[AC=A1C1 и BC=B1C1 и угол С равен углу С1] => треугольник АВС = А1В1С1
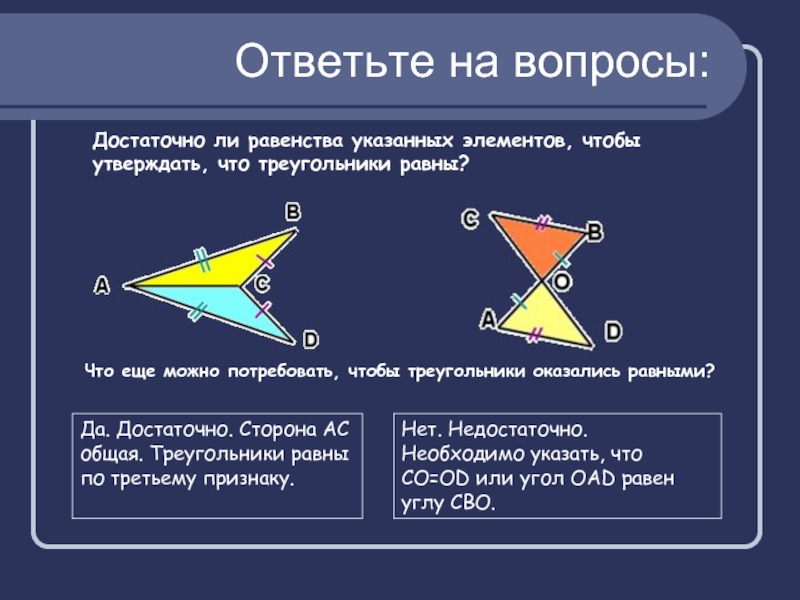
Слайд 4Достаточно ли равенства указанных элементов, чтобы утверждать, что треугольники равны?
Что
еще можно потребовать, чтобы треугольники оказались равными?
Ответьте на вопросы:
Да. Достаточно.
Сторона АС общая. Треугольники равны по третьему признаку.
Нет. Недостаточно. Необходимо указать, что СО=OD или угол ОАD равен углу СВО.
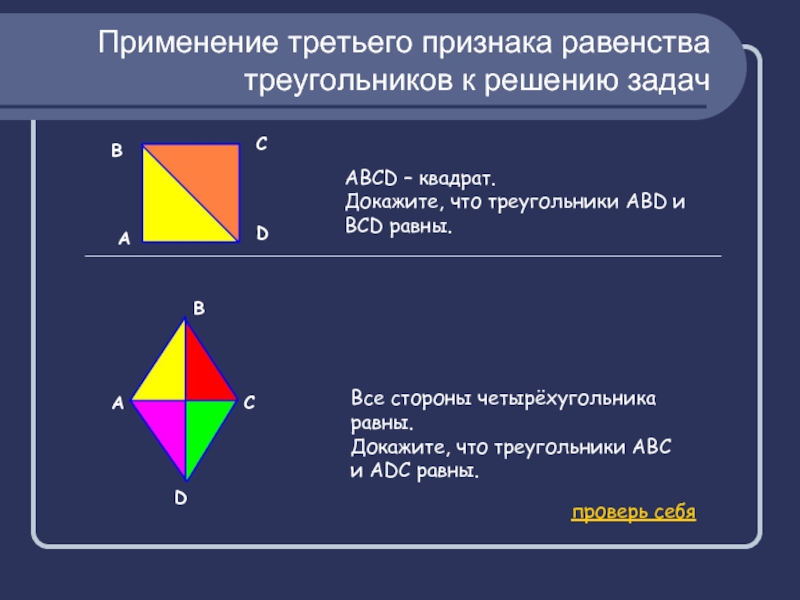
Слайд 5Применение третьего признака равенства треугольников к решению задач
А
АВСD – квадрат.
Докажите,
что треугольники АВD и ВСD равны.
А
С
D
Все стороны четырёхугольника равны.
Докажите, что
треугольники АВС и АDС равны.проверь себя
В
С
D
В
Слайд 6Проверка
А
АВСD – квадрат.
Все стороны квадрата равны и BD - общая.
Треугольники равны по третьему признаку.
А
С
D
Все стороны четырёхугольника равны по условию
и АС - общая.
Треугольники АВС и АDС равны.вернуться
В
С
D
В