Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Содержание
- 1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
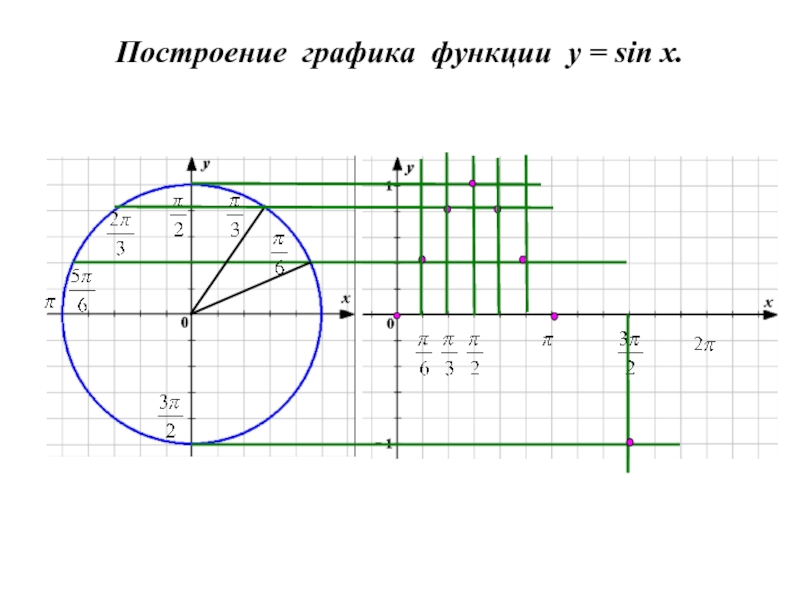
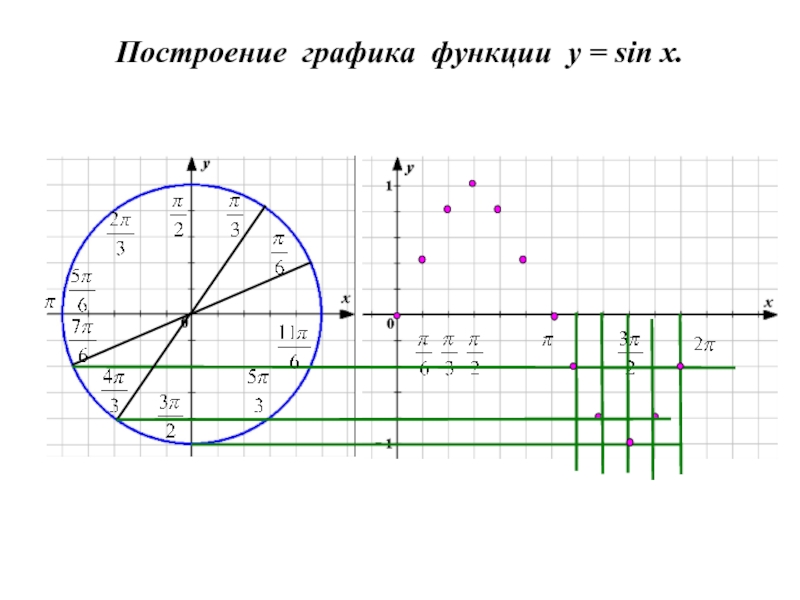
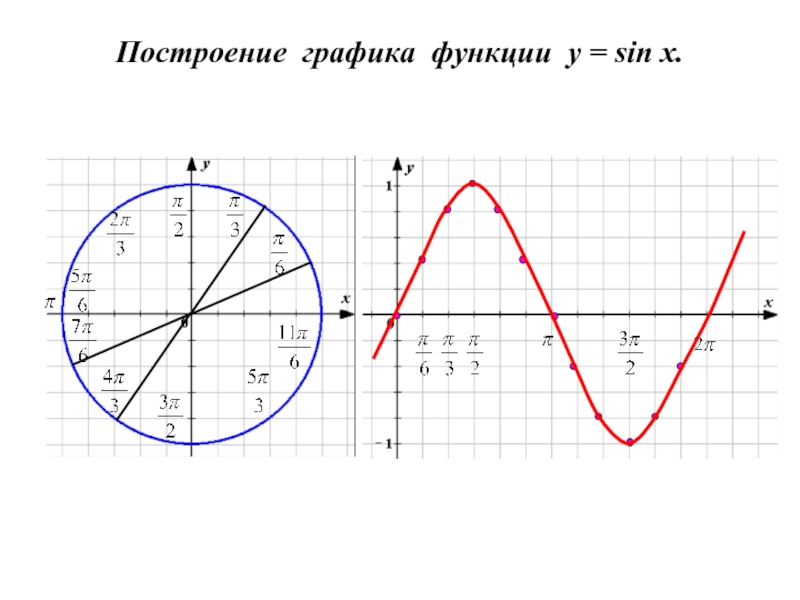
- 2. Построение графика функции y = sin x.
- 3. Построение графика функции y = sin x.
- 4. Построение графика функции y = sin x.
- 5. Функция у = sin x.3. Функция у
- 6. Построение графика функции y = cos x.График
- 7. Функция у = соs x.3. Функция у
- 8. Скачать презентанцию
Построение графика функции y = sin x.
Слайды и текст этой презентации
Слайд 5
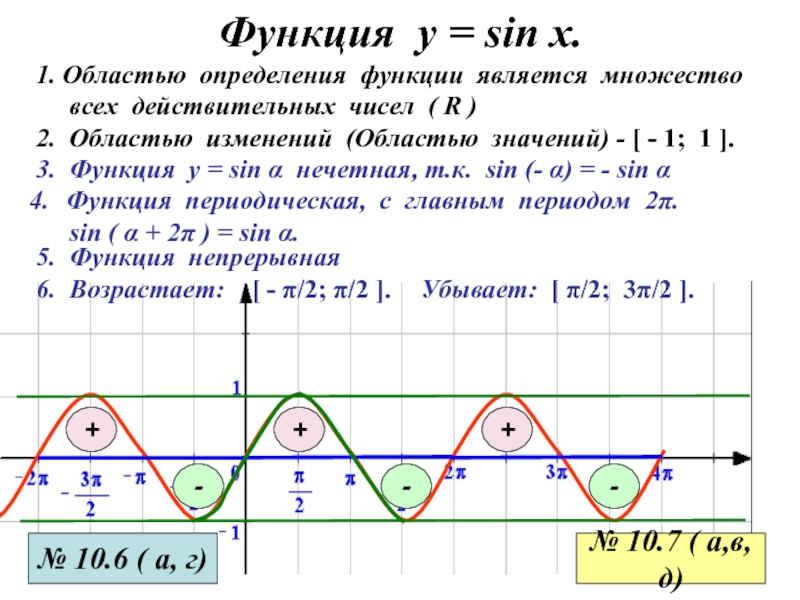
Функция у = sin x.
3. Функция у = sin α
нечетная, т.к. sin (- α) = - sin α
1. Областью
определения функции является множествовсех действительных чисел ( R )
2. Областью изменений (Областью значений) - [ - 1; 1 ].
Функция периодическая, с главным периодом 2π.
sin ( α + 2π ) = sin α.
5. Функция непрерывная
6. Возрастает: [ - π/2; π/2 ].
Убывает: [ π/2; 3π/2 ].
№ 10.6 ( а, г)
№ 10.7 ( а,в,д)
+
+
+
-
-
-
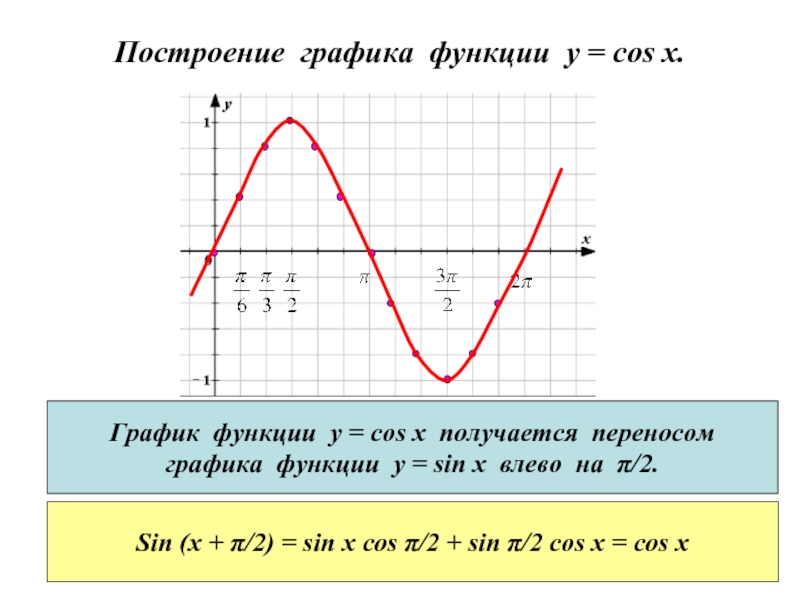
Слайд 6Построение графика функции y = cos x.
График функции у =
cos x получается переносом
графика функции у = sin x влево
на π/2.Sin (x + π/2) = sin x cos π/2 + sin π/2 cos x = cos x
Слайд 7
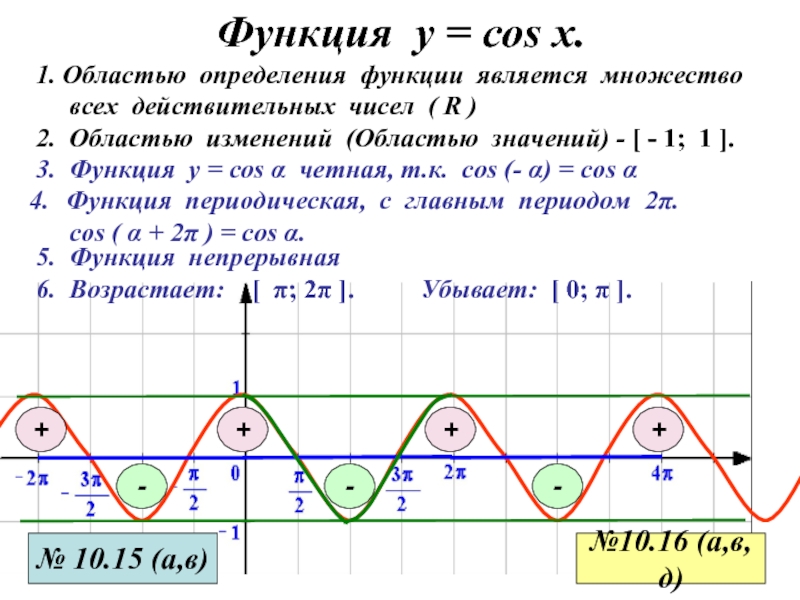
Функция у = соs x.
3. Функция у = cos α
четная, т.к. cos (- α) = cos α
1. Областью определения
функции является множествовсех действительных чисел ( R )
2. Областью изменений (Областью значений) - [ - 1; 1 ].
Функция периодическая, с главным периодом 2π.
cos ( α + 2π ) = cos α.
5. Функция непрерывная
6. Возрастает: [ π; 2π ].
Убывает: [ 0; π ].
№ 10.15 (а,в)
№10.16 (а,в,д)
-
-
-
+
+
+
+
Теги
