Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения и методы их решения
Содержание
- 1. Уравнения и методы их решения
- 2. Показательные уравненияОпред.: Уравнение вида aх=b , называется показательным
- 3. Методы решения:Приведение к одному основаниюРазложение левой части
- 4. Приведение к одному основанию:
- 5. Разложение левой части уравнения на множители:3 х+1
- 6. Замена переменной, приведение к квадратному:9х – 4
- 7. Деление левой и правой частей уравнения на
- 8. Примеры для самопроверки:
- 9. Типовые задания ЕГЭ:1.Решить уравнение:5х=125;2.Решить уравнение:
- 10. 4.Решить уравнение:3х+1 - 2 ·3х-2 =25;5.Решить уравнение:32х–
- 11. 8.Найти промежуток, которому принадлежат все решения уравнения:3
- 12. В4.Найти модуль разности корней:4х-√х²-5 - 12 ·
- 13. Тригонометрические уравнения
- 14. I) Уравнения Cosx=a, a [-1; 1]
- 15. Например. Cosx=, X=+ 2
- 16. II) Уравнения sinx=a, a 1; 1]
- 17. Например. Sinx=,(0; 1) X= (-1)narcsin+nZ X=
- 18. III) Уравнения tgx=a, a tgx=a, a0x=arctga + Ztgx= -a , ax= -arctga + n, nZ
- 19. Например. tgx=,[0;)x=arctg x=+Ztgx= -, -(-; 0) x= -arctg+n, nZx= - +Z
- 20. Методы решения тригонометрических уравнений.
- 21. 2.разложение левой части на множители Cosx=cos3xCosx-cos3x=0-2sin2xsin(-x) =0Sin2x=0
- 22. 3.однородное уравнение 1-ой степени asinx+bcosx=0 Решается делением
- 23. 4.однородное уравнение 2-ой степени asin2x+bsinxcosx+ccos2x=0 asin2x+bsinxcosx+ccos2x=0|:cos2x0atg2x+btgx+c=0tgx=t,
- 24. 5. Уравнение вида asinx+bcosx=c asinx+bcosx=cSinx +cosx=
- 25. Уравнения для самостоятельной работы! Базовый уровень Sinx=Cosx=-tgx=1+sin()=0Sin2x=Sinx+cosx=02cos(2x-)=Sin(x-)=0+1=0tgx-1=0
- 26. Повышенный уровень 2sin2x+3sinxcosx-2cos2x=0=03sinx+4cosx=10Sinx-sin2x+sin3x-sin4x=0Sinx-sin2x+sin3x-sin4x=0Cosx+cos=Sin3x-sin9x=0tg(3x+600)= ctg( -1)sin(-1)ctgx=04sincos=-Sinx-cosx=4sinxcos2x
- 27. Трудные задания Cos2x+cos22x+cos23x+cos24x=2(cos6x-1)ctg3x=sin3xCos(x+)+sin2x=-2Cos2x+|cosx|sinx=0Cos2x+sin22x+cos23x=(cos2x + 3 sinx-4)=0=0cosx+2sinx)=1-1=4sinx+ ctgxtg=0
- 28. Трудные заданияcosx-cos3x+2=0 удовлетворяющие условие: |x+|+2cosx=0=0,удовлетворяющие условию |x| –= -4+ =8
- 29. Уравнение с модулем Определение: a a
- 30. Методы решений. По определению модуля:|x+1|=3 =и = ==>x=-4
- 31. метод интервалов:|x+1| + |x-1| + |x+10|=121.найдём корни
- 32. метод интервалов:3.= = x=посторонний корень == =
- 33. метод интервалов: = ==x=– посторонний кореньОтвет:x1=-2 x2=0
- 34. Базовый уровень 1.|x+3|=122. x+5=|x|3. |x-15|=25x4.|2x|=1005.|x-40|=806.|x|=57. |x|=3x+108. |3x-9|=1
- 35. Повышенный уровень 1.| -
- 36. Логарифмические уравнения
- 37. При решение логарифмических уравнений применяют, такие преобразования,
- 38. логарифмическихМетодырешенияуравнений.
- 39. 1)Решение логарифмических уравнений на основании определения логарифма.(2x+1)=22x+1=2x+1=9X=4 (2×4+1)=Проверка9=2Ответ:х=4
- 40. 2)Метод приведения логарифмических уравнений к квадратному.(+1)=2ОДЗ: ==
- 41. 3) Метод потенцирования )ОДЗ = = =0Применяя метод потенцирования, получилиХ=6-+х-6=0=2, =-3 –п.кОтвет:х=2
- 42. 4)Метод приведения логарифмов к одному основанию. Используя
- 43. 5)Метод логарифмирования ОДЗ: = =x == 1+, 21+ 2X=3ОДЗ
- 44. Решить уравнение показательные по образцу.-6=4ОДЗ:== Ответ: Х
- 45. =6+2х-= Ответ:х=-1,х=21) =0 2) 3)
- 46. Решить логарифмические уравнения, упростив правую часть.1) 2) 3) 4)
- 47. Решить уравнение по образцу 2 Х=0∉ОДЗ , х=Ответ: х=
- 48. Решите уравнения, приведя к логарифмам с одинаковыми основаниями. lg (x+2) + 3+26)=03) +log3(-x-1)=02+x-5)+=log3-log4 =-9
- 49. Решить уравненияXlog3x-3=0,1x1+lgx=1Xlog4x=23(log4x+3)=0log3x-log3(x+8)=-log3(x+3)log2(x+1)+log2(x+2)=12log4(4-x)=4-log2(-2-x)log2(x+1)=1+2log2xlg(x+)-lg(x-)=lg(x+6)-lgxlog2 -1=log25x2-8x+5=0Log2 (24-x-2x+7)=3-x2log2(1-)=3log2(2+)+124log7(()0,75) = X2log2x+3 -6=0-4+log2(5-log0,2125)x2-x=0Log22Log2(log5x)=12+7=0Lg2(x+1)=lg(x+1)lg(x-1)+2lg2(x-1)3log2x2-log22(-x)=5logxlog25x=-1log3|x+8|+log3x4=2
- 50. Решить уравнениеLog3x+7(9+12x+4x2)+log2x+3(6x2+23x+21)=4log(100x3)lg=8log6(x+5)+log6x2=1=Log3(x+2)(5x)-log3Log4log2x+log2log4x=2-log77=4-log24=log77xlg+lglog23x+ log2x3+3log3x+3logx3=22log3xlog2x+2log3x-log2x-1=0
- 51. Метод монотонности функций.Теорема 1. Если одна из
- 52. Алгоритм решения уравнения методом использования монотонности.1.Иследовать на
- 53. , возрастает функция и -возрастающая и ()-возрастающая
- 54. Х=1 ,+ Х=4,--функция убывает, а-возрастает, теорему не
- 55. Уравнение с завуалированным обратным числом.()x +()x=8(4+)=16-16=1=4+=tt ()
- 56. Например! ()x + ()x=6( )x + ()x=10
- 57. Используемая литератураС.М.Никольский- алгебра 10-11классШ.А.Алимов и др- алгебра
- 58. Скачать презентанцию
Показательные уравненияОпред.: Уравнение вида aх=b , называется показательным
Слайды и текст этой презентации
Слайд 1Уравнения и методы их решения
Над проектом работали:
Маслов Андрей
Мулярчук Екатерина
Фадеенко Виктор
МКОУ
СОш с Красное 2014
Слайд 3Методы решения:
Приведение к одному основанию
Разложение левой части уравнения на множители
(выносим степень с наименьшим показателем)
Замена переменной, приведение к квадратному (подстановка)
Деление
левой и правой частей уравнения на степень
Слайд 5Разложение левой части уравнения на множители:
3 х+1 - 2 ·
3 х-2 =25
3 х-2(3³-2)=25
3 х-2 · 25=25 |:25
3 х-2 = 1
3 х-2 = 30=>х-2=0
х=2
Слайд 6Замена переменной, приведение к квадратному:
9х – 4 · 3х –
45=0
32х– 4 ·3х -45=0
3х =t=>t²-4t-45=0
t1+t2 =4 t1 =9
t1 +t2 =45 t2 =-5п.к.
3х =9
3х =3²=>х=2
Слайд 7Деление левой и правой частей уравнения на степень:
3х = 52х
3х
= 25 х |÷3х
1= 25 х 3
25 º 25 х =>x=0
3 3
Слайд 8Примеры для самопроверки:
1 0,5х-1 9;
7 ·
5х– 5х+1 = 2 · 5-3;27
2х² + 14 · 2х +1 – 29=0;
7х +6 · 3х +6=73х·33х
Слайд 9Типовые задания ЕГЭ:
1.Решить уравнение:
5х=125;
2.Решить уравнение:
1 0,1х-1_ 16;
32 ¯3.Указать промежуток, которому принадлежит корень уравнения:
3х²+х-12 = 1;
Слайд 10
4.Решить уравнение:
3х+1 - 2 ·3х-2 =25;
5.Решить уравнение:
32х– 4 ·3х– 45=0;
6.Решить
уравнение:
32х-1 – 22х-1 = 0;
7.Решить уравнение:
32х+5– 22х+7 + 32х+4 -
22х+4= 0;
Слайд 118.Найти промежуток, которому принадлежат все решения уравнения:
3 · 16х +
2 · 81х =5 · 36х;
9.Указать промежуток, которому принадлежит корень
уравнения:52х– 4 · 5х– 5 = 0;
10.Решить уравнение:
3Sin²x + 3Cos²x = 4
Слайд 12В4.Найти модуль разности корней:
4х-√х²-5 - 12 · 2х-1-√х²-5 + 8
= 0;
В5.Решить уравнение:
23х-1 · 53х-1 = 100;
В6.Решить уравнение:
√3 ·
2х − 4х − 2 = 1−2х;В7.Решить уравнение:
32х+3 · 33х+1 · 625х+2 = 600х+7;
Слайд 14I) Уравнения Cosx=a, a [-1; 1]
а) Cosx=a,
а
(0; 1)
X=
аrccosa +2
n , n
б)Cosx=a, a
(-1;0)
X=
(
-arccosa) +2
Cosx=0
Cosx=-1
,
X=
+2
n
X=
+2
Cosx=1
X=2
![I) Уравнения Cosx=a, a [-1; 1] а) Cosx=a, а(0; 1)X=аrccosa +2 n , nб)Cosx=a,](/img/thumbs/1ef0e1a6181866567dcdaa1bd05562bb-800x.jpg "Уравнения и методы их решения I) Уравнения Cosx=a, a [-1; 1] а) Cosx=a, а(0; 1)X=аrccosa")
Слайд 16II) Уравнения sinx=a, a 1; 1]
Sinx=a, a
(0; 1)
X=
(-1)narcsina +
n, n
Z
Sinx=a, a
(-1;0)
X= (-1)n+1arcsina+
n, n
Z
Sinx= 0
X=
n, n
Z
Sinx= 1
X=
+2
K, k
Z
Sinx= -1
X= -
+ 2
n, n
![II) Уравнения sinx=a, a 1; 1] Sinx=a, a (0; 1)X= (-1)narcsina + n, nZSinx=a, a(-1;0)X= (-1)n+1arcsina+n,](/img/thumbs/3904d026da879302059d5c4b304143c8-800x.jpg "Уравнения и методы их решения II) Уравнения sinx=a, a 1; 1] Sinx=a, a (0; 1)X= (-1)narcsina")
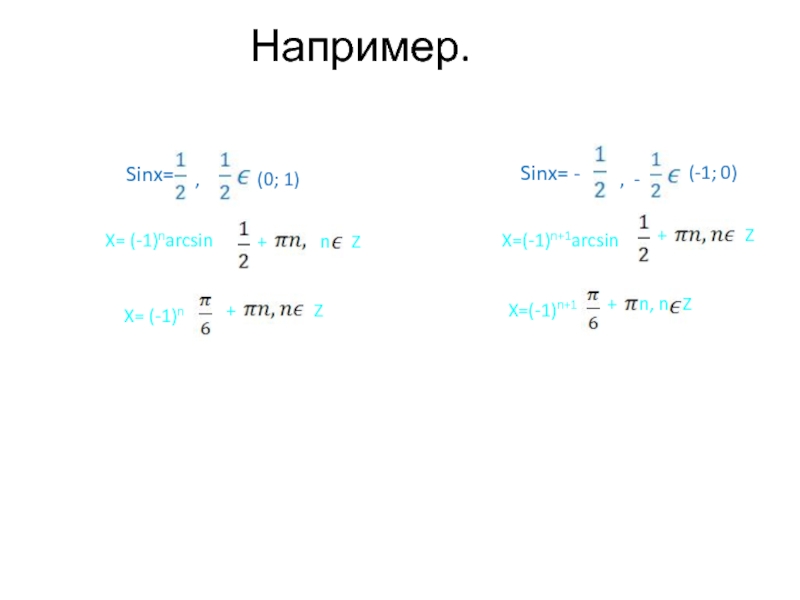
Слайд 17Например.
Sinx=
,
(0; 1)
X= (-1)narcsin
+
n
Z
X= (-1)n
+
Z
Sinx= -
,
-
(-1; 0)
X=(-1)n+1arcsin
+
Z
X=(-1)n+1
+
n, n
Z
Слайд 20Методы решения тригонометрических уравнений.
1)Уравнения, сводящиеся к квадратным
а)
Sin2x + sinx – 2=0
Sinx=t, t
[-1;1]
t2 +t-2=0
t1=1, t2=-2-п.к
так-1; 1]
как -2∉
sinx=1,
x=
+ 2
![Методы решения тригонометрических уравнений. 1)Уравнения, сводящиеся к квадратныма) Sin2x + sinx – 2=0Sinx=t, t[-1;1]t2](/img/thumbs/5f804172bc68ed2d5fd9010a227248cc-800x.jpg "Уравнения и методы их решения Методы решения тригонометрических уравнений. 1)Уравнения, сводящиеся к квадратныма) Sin2x +")
Слайд 212.разложение левой части на множители
Cosx=cos3x
Cosx-cos3x=0
-2sin2xsin(-x) =0
Sin2x=0
или
sinx=0
x=
2x=
X=
n
,
Слайд 223.однородное уравнение 1-ой степени asinx+bcosx=0
Решается делением на cosx0
0
+
= 0
sinx+cosx=0 |:cosx
atgx+b=0
x=-arctg
+
tgx+1=0
tgx=-1
+
x=-arctg1
n, n
Z
x=-
+
Слайд 234.однородное уравнение 2-ой степени asin2x+bsinxcosx+ccos2x=0
asin2x+bsinxcosx+ccos2x=0
|:cos2x
0
atg2x+btgx+c=0
tgx=t, at2+bt+c=0
Д=b2-4ac
t1,2=
tgx=
x1=arctg(
) +
n
x2= arctg(
)
+
n
3sin2x-7sinxcosx+2cos2x=0|:cos2x
0
3tg2x-7tgx+2=0
tgx=t, 3t2-7t+2=0
Д= b2-4ac=25, Д
t1,2=
tgx=2
tgx=
x=arctg2+
x=arctg
+
k,
k
Z
Слайд 245. Уравнение вида asinx+bcosx=c
asinx+bcosx=c
Sinx +
cosx=
=cos
=sin
Cos
+ sin
cosx=
Sin (
+ x) =
X= (-1)narcsin
-
+
z
n, n
Sinx-cosx=1
=
sinx –
cosx=
Sin( -
x
)=
X -
=
(-1)n
+
, n
Z
X= (-1)n
+
+
Слайд 25Уравнения для самостоятельной работы!
Базовый уровень
Sinx=
Cosx=-
tgx=
1+sin(
)=0
Sin2x=
Sinx+cosx=0
2cos(2x-
)=
Sin(x-
)=0
+1=0
tgx-1=0
Слайд 26Повышенный уровень
2sin2x+3sinxcosx-2cos2x=0
=0
3sinx+4cosx=10
Sinx-sin2x+sin3x-sin4x=0
Sinx-sin2x+sin3x-sin4x=0
Cosx+cos
=
Sin3x-sin9x=0
tg(3x+600)=
ctg(
-1)sin(
-1)ctgx=0
4sin
cos
=
-
Sinx-cosx=4sinxcos2x
Слайд 27Трудные задания
Cos2x+cos22x+cos23x+cos24x=2
(cos6x-1)ctg3x=sin3x
Cos(x+
)+sin2x=-2
Cos2x+
|cosx|sinx=0
Cos2x+sin22x+cos23x=
(cos2x + 3
sinx-4)=0
=0
cosx+2sinx)=1
-1=4sinx
+ ctgxtg
=0
Слайд 28Трудные задания
cosx-cos3x+2
=0
удовлетворяющие условие:
|x+
|
+2cosx=0
=0,
удовлетворяющие условию |x|
–
= -4
+
=8
Слайд 31метод интервалов:
|x+1| + |x-1| + |x+10|=12
1.найдём корни подмодульных выражений:
X=-1
x=1
x=-102.нанесём корни на числовую ось
-10 -1 1
Слайд 34Базовый уровень
1.|x+3|=12
2. x+5=|x|
3. |x-15|=25x
4.|2x|=100
5.|x-40|=80
6.|x|=5
7. |x|=3x+10
8. |3x-9|=1
Слайд 35Повышенный уровень
1.|
-
– 5
=
2.|x2-5x+6|=x+1
3.|x-3|+2|x+1|=4
4.|5-2x|+|x+3|=2-3x
5.
=|x|+2
6. x|x|+7x+12=0
7. x2-5x -
8. x2-|3x-5|=5|x|
9. |x+5|=|2x-3-x2|
10. 3|2x2+4x+1|=|x2+5x+1|
11.|2x-y-3|+|x+5y-7|=0
Слайд 37При решение логарифмических уравнений применяют, такие преобразования, которые не приводят
к потери корней, но могут привести к приобретению посторонних корней.
Поэтому проверка каждого из полученных корней путем подстановок и их в исходное уравнение обязательно, если нет уверенности в равносильности уравнений. Проверку найденных корней можно заменить нахождением области определения уравнений. Тогда корнями уравнения, будут те числа, которые принадлежат этой области.
Слайд 391)Решение логарифмических уравнений
на основании определения логарифма.
(2x+1)=2
2x+1=
2x+1=9
X=4
(2×4+1)=
Проверка
9=2
Ответ:х=4
Слайд 402)Метод приведения логарифмических уравнений к квадратному.
(
+1)=2
ОДЗ:
=
=
X
По определению
логарифма
(x+1
=2
+1
+2x+1=
+1
-2x=0
=0
=2
Ответ: х=2
Слайд 413) Метод потенцирования
)
ОДЗ
=
=
=
0
Применяя метод потенцирования, получили
Х=6-
+х-6=0
=2,
=-3 –п.к
Ответ:х=2
Слайд 424)Метод приведения логарифмов к одному основанию. Используя формулу
=2n
f(x)
Где
а
,а
1,n
z.
=2n|
|,
где a
,
a
.
ОДЗ:
-5
0 +5x-6=0
+
=-5
=-6
Слайд 44Решить уравнение показательные по образцу.
-6
=4
ОДЗ:
=
=
Ответ: Х =1
)=
ОДЗ:
р.м.п
У=
У=0=
Д=4+24=28
=
х
1-
;
;
Слайд 48 Решите уравнения, приведя к логарифмам с одинаковыми основаниями.
lg
(x+2) +
3+26)=0
3) +log3(-x-1)=0
2+x-5)+
=log3
-log4
=-9
Слайд 49Решить уравнения
Xlog3x-3=
0,1x1+lgx=1
Xlog4x=23(log4x+3)=0
log3x-log3(x+8)=-log3(x+3)
log2(x+1)+log2(x+2)=1
2log4(4-x)=4-log2(-2-x)
log2(x+1)=1+2log2x
lg(x+
)-lg(x-
)=
lg(x+6)-
lgx
log2
-1=log2
5x2-8x+5
=0
Log2 (24-x-2x+7)=3-x
2log2(1-
)=3log2(2+
)+12
4log7(
(
)0,75)
=
X2log2x+3
-6=0
-4+log2(5-log0,2125)x2-x=0
Log2
2
Log2(log5x)=1
2
+7=0
Lg2(x+1)=lg(x+1)lg(x-1)+2lg2(x-1)
3log2x2-log22(-x)=5
logx
log25x=-1
log3|x+8|+
log3x4=2
Слайд 50Решить уравнение
Log3x+7(9+12x+4x2)+log2x+3(6x2+23x+21)=4
log(100x3)lg
=8
log6(x+5)+
log6x2=1
=
Log3(x+2)(5x)-log3
Log4log2x+log2log4x=2
-log77=
4
-log24=log77x
lg
+lg
log23x+ log2x3+3log3x+3logx3=2
2log3xlog2x+2log3x-log2x-1=0
Слайд 51Метод монотонности функций.
Теорема 1. Если одна из функций возрастает, а
другая убывает
на промежутке, то уравнение f(x)=g(x) имеет не более
одного корня.Теорема 2. Если одна функция возрастает (убывает), а вторая принимает
постоянные значения на некотором промежутке, то уравнение
имеет не более одного корня.
Слайд 52Алгоритм решения уравнения методом использования монотонности.
1.Иследовать на монотонность функции f(x)
и g(x) в О.О.У
2.Если выполняются условия теоремы f(x) и g(x)
и удается подобрать удовлетворяющие уравнению f(x)=g(x), то
-единственный корень
этого уравнения
, (
)-функция возрастает т.к
возрастает и
возрастает и в правой части уравнения постоянная функция, то
уравнения имеет один корень.
9+16=25
25=25
Слайд 53,
возрастает функция и
-возрастающая и
(
)-возрастающая функция ,в правой
части постоянная
функция.
Х=1, 6- 4
Х=2, 36-16
Х=3 , 216-64=152
Слайд 54Х=1 ,
+
Х=4,
-
-функция убывает, а
-возрастает, теорему не применять
Ф.М.У
а=
У=х-4,а=1
прямая направлена
Применяем теорему: уравнений имеет один корень
Х=3 ,
-1=-1,
Х=3
Слайд 55Уравнение с завуалированным обратным числом.
(
)x +(
)x=8
(4+
)=16-16=1=
4+
=t
t (
) =1=
4-
=
t+
=8|
t
t2-8t+1=0
д=b2-4ac=64-4=60
t1,2=
=
=4
(
)x=(4+
)
(
)x=(4-
)
=1
= -1
X=2 x= -2
Слайд 57Используемая литература
С.М.Никольский- алгебра 10-11класс
Ш.А.Алимов и др- алгебра 10-11класс
Справочник по математике
5-11 класс
Т.С. Кармакова -элективный курс «Методы решения нестандартных уравнений»
