Урок одной задачи.Вписанная и описанная окружность.

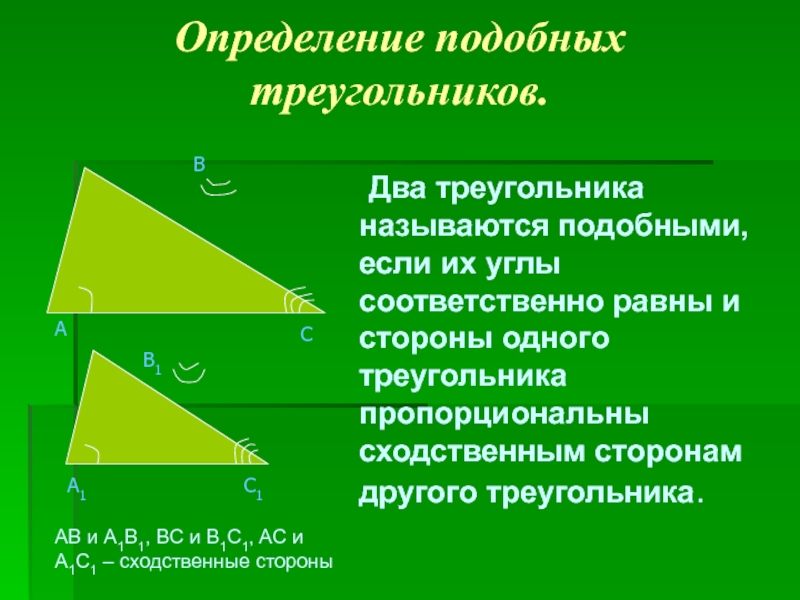
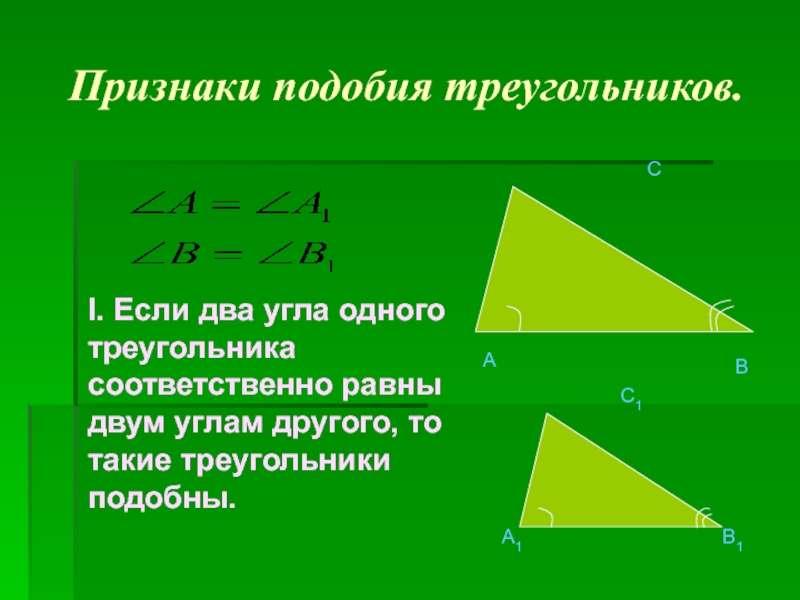
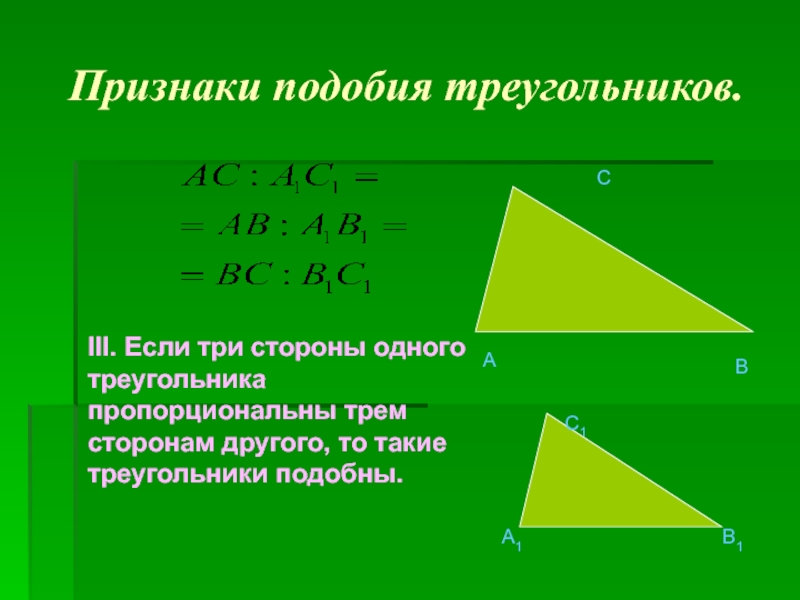
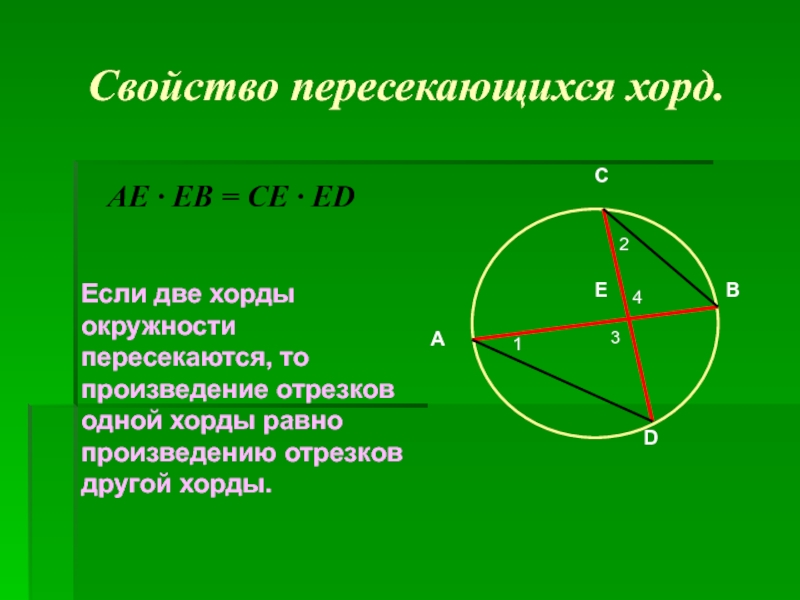
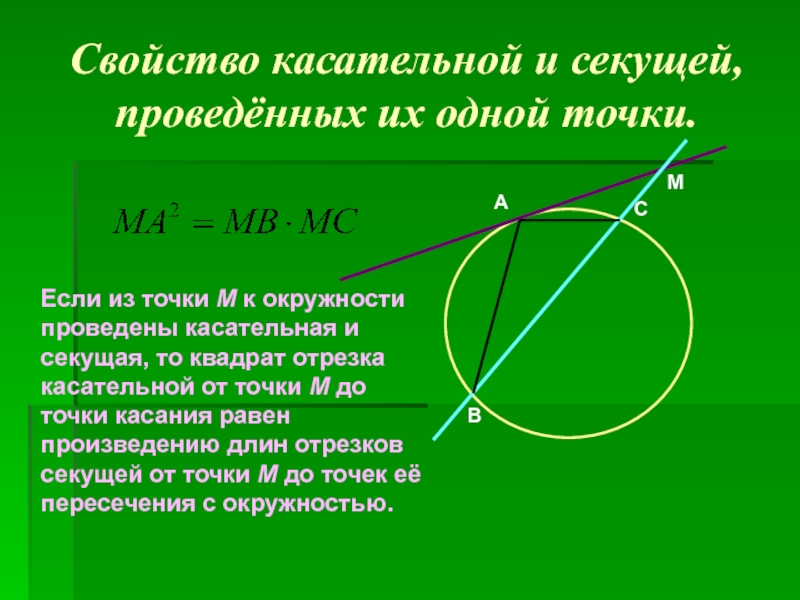
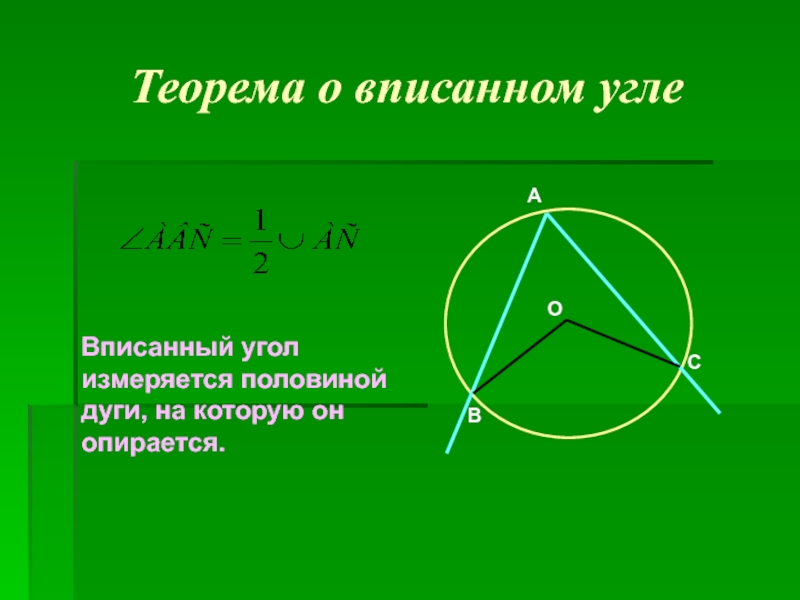
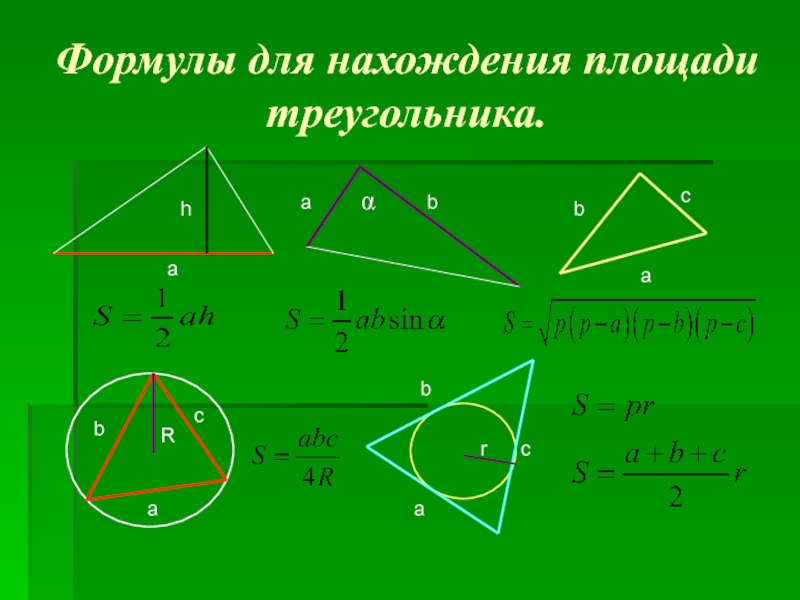
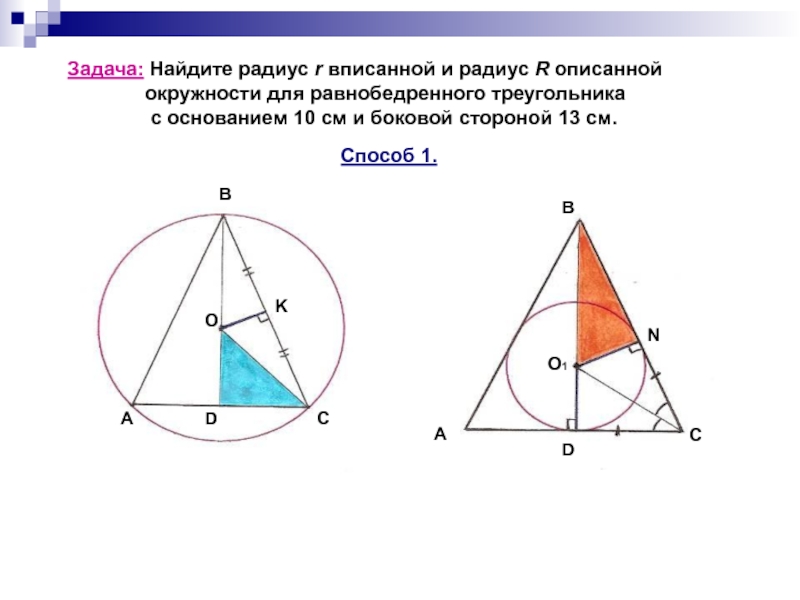
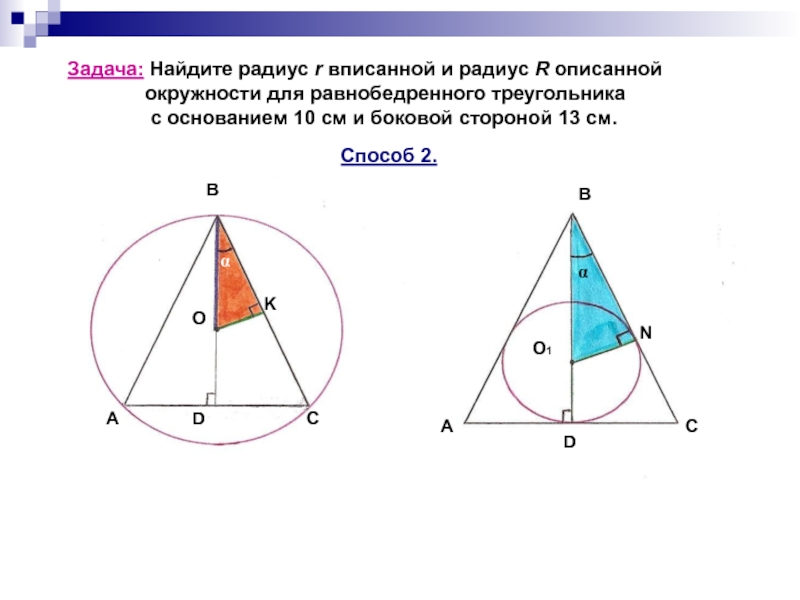
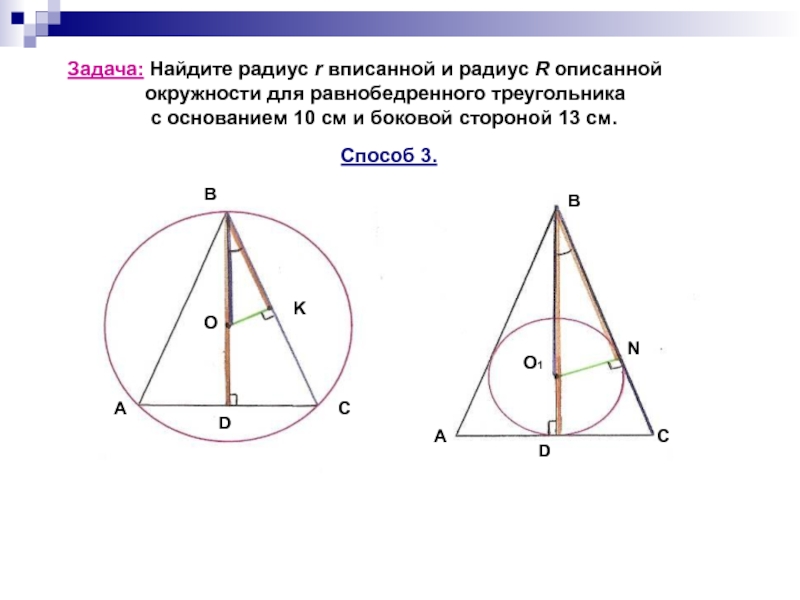
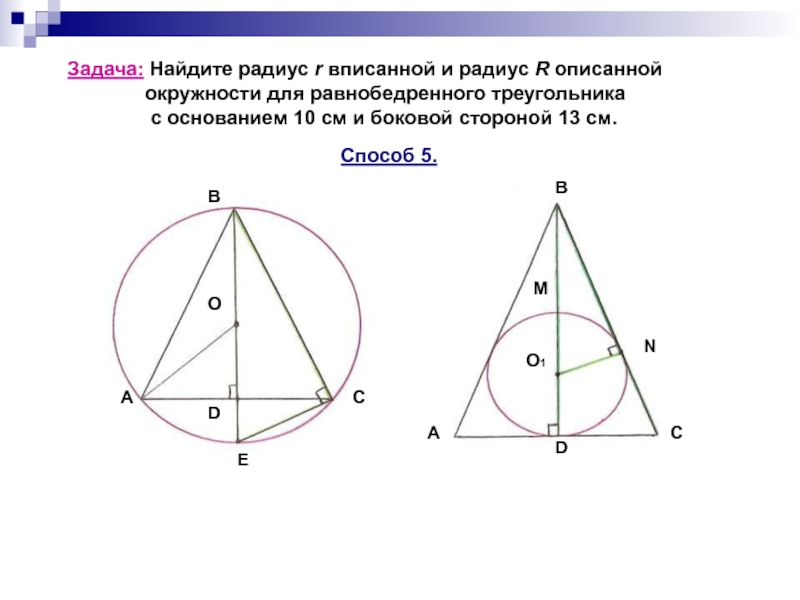
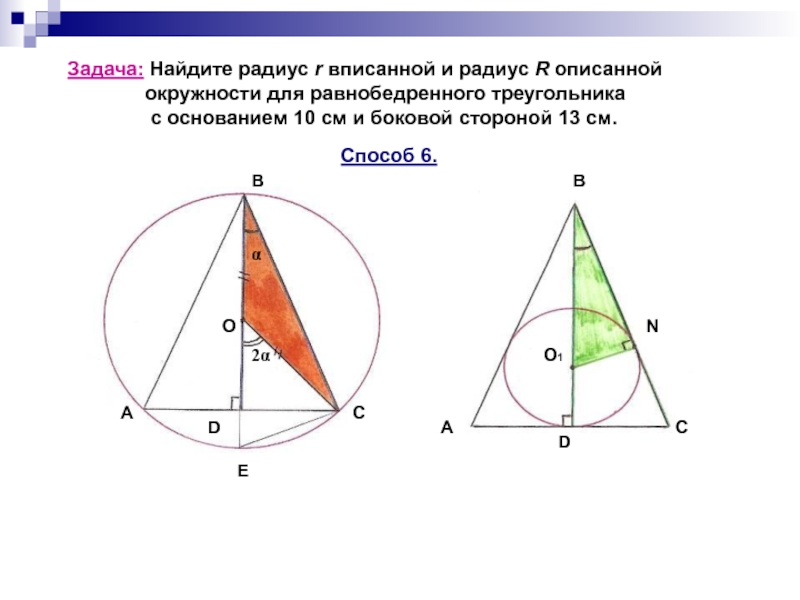
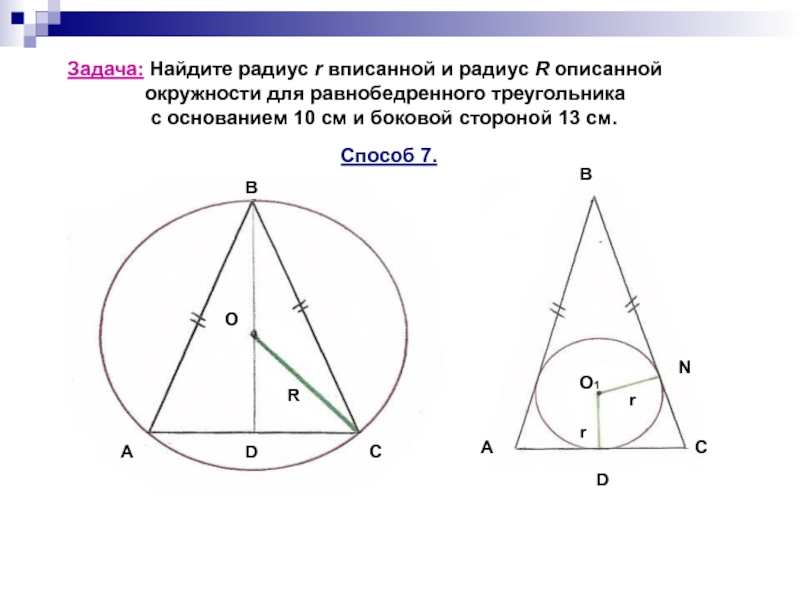
задачи.)».
Цель урока: обобщить и систематизировать знания по

теме «вписанная и описанная окружность».

Задачи урока: привитие навыков в отыскании различных способов решения задач, развитие исследовательских способностей у учащихся.

Учитель МБОУ СОШ №92 г. Кемерово Денисова Татьяна Александровна

задачи.)».
План урока: 1. Постановка цели и задач

урока.
2. Повторение. Подготовка
к решению задачи.
3. Решение одной задачи
несколькими способами.
4. Подведение итогов урока.
5. Домашнее задание.

равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.














С
А
В
A1
C1
B1
AB

и A1B1, BC и B1C1, AC и A1C1 – сходственные стороны

другого, то такие треугольники подобны.
Признаки подобия треугольников.

треугольника и углы, заключённые между этими сторонами, равны, то такие

треугольники подобны.

Признаки подобия треугольников.

то такие треугольники подобны.
Признаки подобия треугольников.

сторонам.
Свойство биссектрисы угла треугольника.

D

одной хорды равно произведению отрезков другой хорды.
АЕ · ЕВ

= СЕ · ЕD

М к окружности проведены касательная и секущая, то квадрат отрезка

касательной от точки М до точки касания равен произведению длин отрезков секущей от точки М до точек её пересечения с окружностью.

он опирается.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 1.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 2.

α

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 3.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 4.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 5.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 6.

окружности для равнобедренного треугольника

с основанием 10 см и боковой стороной 13 см.

Способ 7.

единственная цель – найти правильный ответ.

Если же требуется применить при этом несколько способов, стараешься отыскать наиболее оригинальное, красивое, экономичное решение.
Для этого приходится вспоминать многие теоретические факты, методы и приёмы, анализировать их с точки зрения применимости к данной в задаче ситуации, накапливается определённый опыт применения одних и тех же знаний к различным вопросам.
Всё это активизирует учебную деятельность, прививает интерес к предмету.

Подведение итогов урока.