Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямых и плоскостей.
Содержание
- 1. Параллельность прямых и плоскостей.
- 2. Параллельные прямые в пространстве.Две прямые в пространстве
- 3. Теорема.Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.Aba
- 4. Признак параллельности прямых.Две прямые параллельные третьей прямой параллельны.abc
- 5. Задача №1.Прямые a и b не лежат
- 6. Признак параллельности прямой и плоскости.Прямая и плоскость
- 7. Признак параллельности плоскостей.Две плоскости называются параллельными, если
- 8. Задача №2.Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости.α ba b1 a1β
- 9. Существование плоскости, параллельной данной плоскости.Через точку вне
- 10. Свойства параллельных плоскостей.Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.αβγab
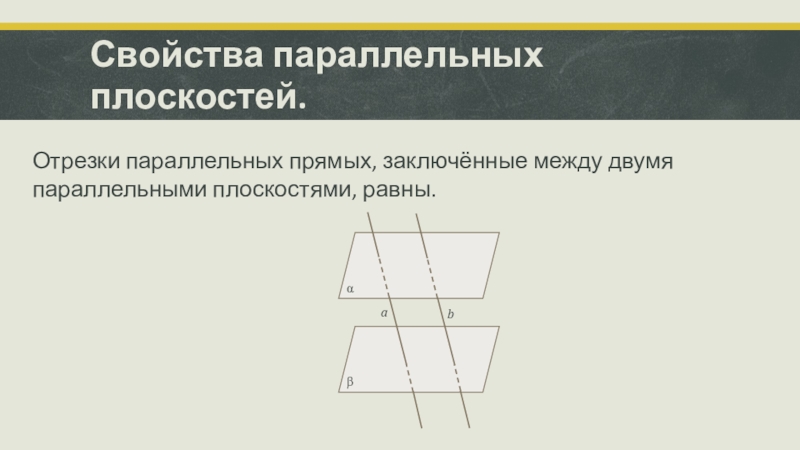
- 11. Свойства параллельных плоскостей.Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.αβab
- 12. Свойство транзитивности.Если две плоскости параллельны третьей, то они параллельны между собой.
- 13. Задача №3.Дано:α ∥ β AB ∩ AC =
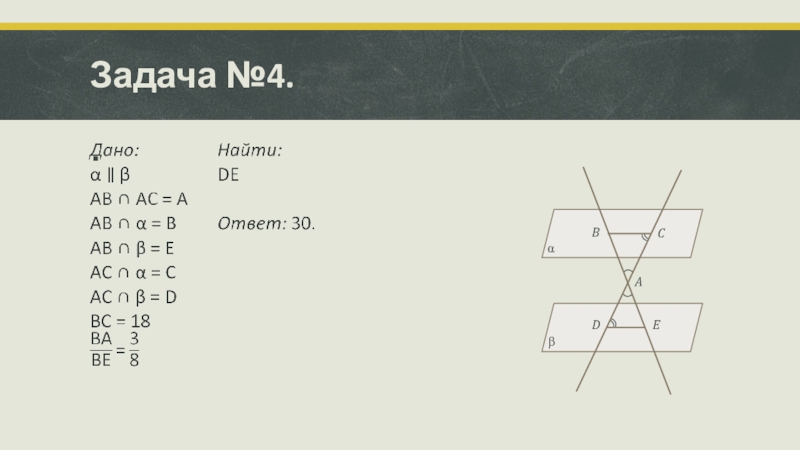
- 14. Задача №4.βADECBα
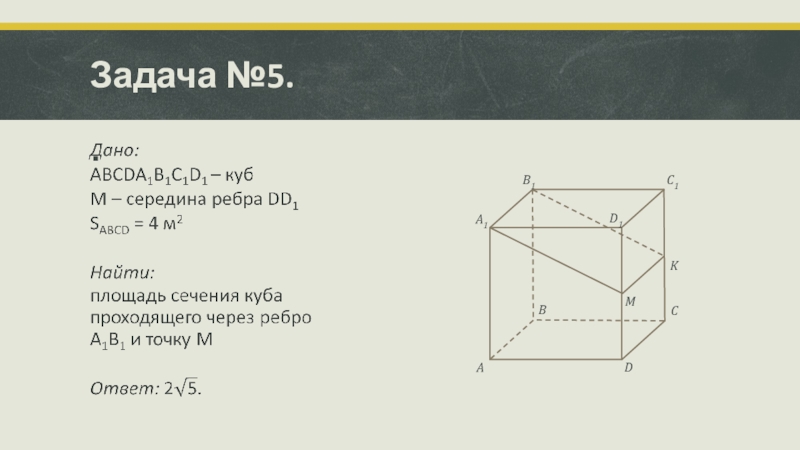
- 15. Задача №5.ABCDMKA1B1C1D1
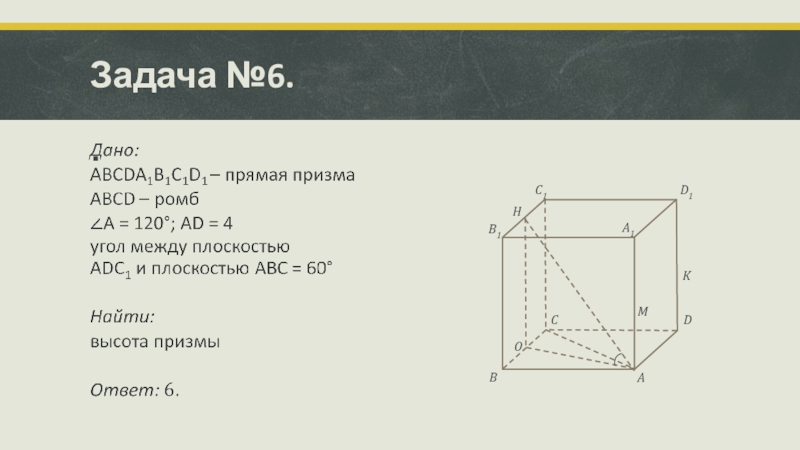
- 16. Задача №6.BCDAMKB1C1D1A1HO
- 17. Слайд 17
- 18. Скачать презентанцию
Параллельные прямые в пространстве.Две прямые в пространстве называются параллельными (рис. 1), если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются
Слайды и текст этой презентации
Слайд 2Параллельные прямые в пространстве.
Две прямые в пространстве называются параллельными (рис.
1), если они лежат в одной плоскости и не пересекаются.
Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися (рис. 2).α
α
a
b
b
a
1
2
Слайд 3Теорема.
Через точку вне данной прямой можно провести прямую, параллельную этой
прямой, и притом только одну.
A
b
a
Слайд 5Задача №1.
Прямые a и b не лежат в одной плоскости.
Можно ли провести прямую c, параллельную прямым a и b?
Слайд 6Признак параллельности прямой и плоскости.
Прямая и плоскость называются параллельными, если
они не пересекаются, то есть не имеют общих точек.
Если прямая,
не принадлежащая плоскости, параллельная какой-нибудь прямой в этой плоскости, то она параллельная и самой плоскости.Слайд 7Признак параллельности плоскостей.
Две плоскости называются параллельными, если они не пересекаются,
то есть не имеют общих точек.
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.a
b
a’
b’
α
β
Слайд 8Задача №2.
Докажите, что через две скрещивающиеся прямые можно провести параллельные
плоскости.
α
b
a
b1
a1
β
Слайд 9Существование плоскости, параллельной данной плоскости.
Через точку вне данной плоскости можно
провести плоскость, параллельную данной, и притом только одну.
α
β
A
Слайд 10Свойства параллельных плоскостей.
Если две параллельные плоскости пересекаются третьей, то прямые
пересечения параллельны.
α
β
γ
a
b
Слайд 11Свойства параллельных плоскостей.
Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями,
равны.
α
β
a
b
Слайд 12Свойство транзитивности.
Если две плоскости параллельны третьей, то они параллельны между
собой.
Слайд 13Задача №3.
Дано:
α ∥ β
AB ∩ AC = A
AB ∩ α
= B
AB ∩ β = D
AC ∩ α = C
AC
∩ β = EAC = 3
CE = 4
DE = 21
Найти:
BC
Ответ: 9.
A
C
B
D
E
α
β