Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Развитие понятия числа 6 класс
Содержание
- 1. Развитие понятия числа 6 класс
- 2. В основе курса обучения математике по системе
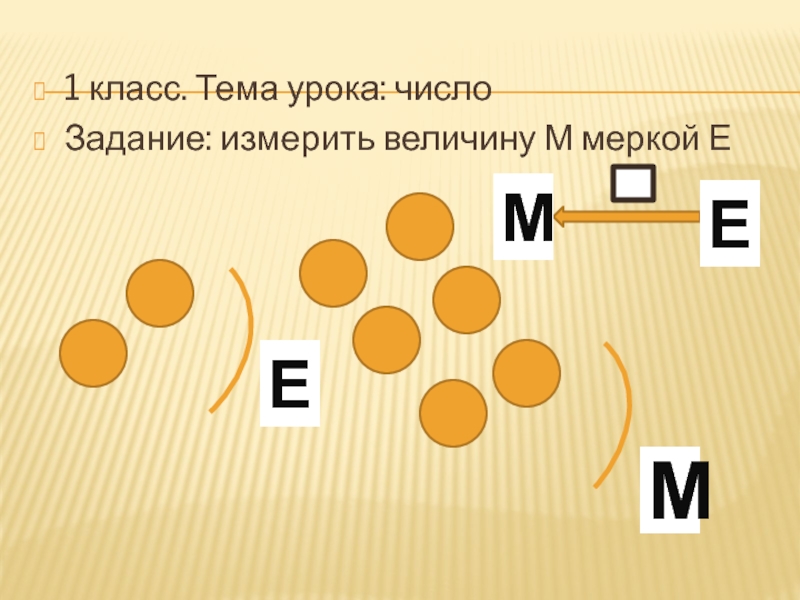
- 3. 1 класс. Тема урока: числоЗадание: измерить величину М меркой ЕМ ЕМЕ
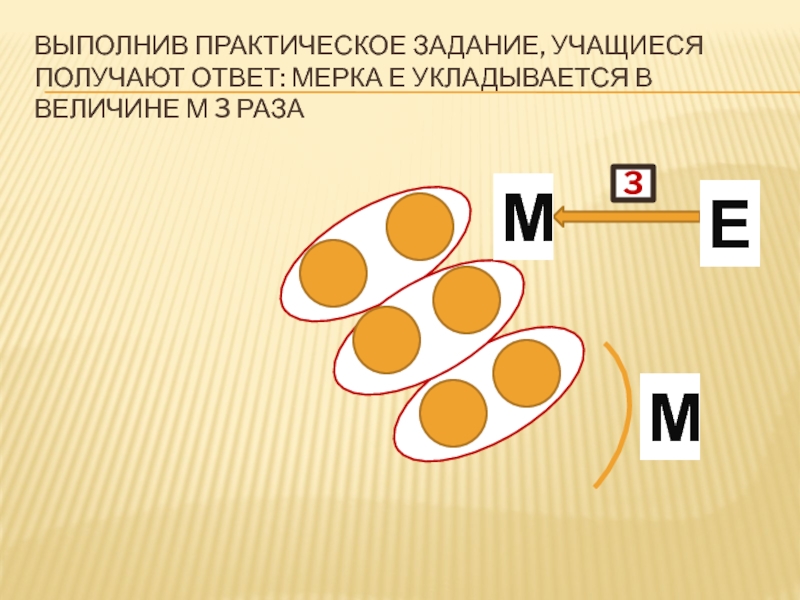
- 4. Выполнив практическое задание, учащиеся получают ответ: мерка Е укладывается в величине М 3 разаМЕ3М
- 5. МЕЕЕЕЗадание: измерить величину М меркой Е5 класс. Тема: измерение величин
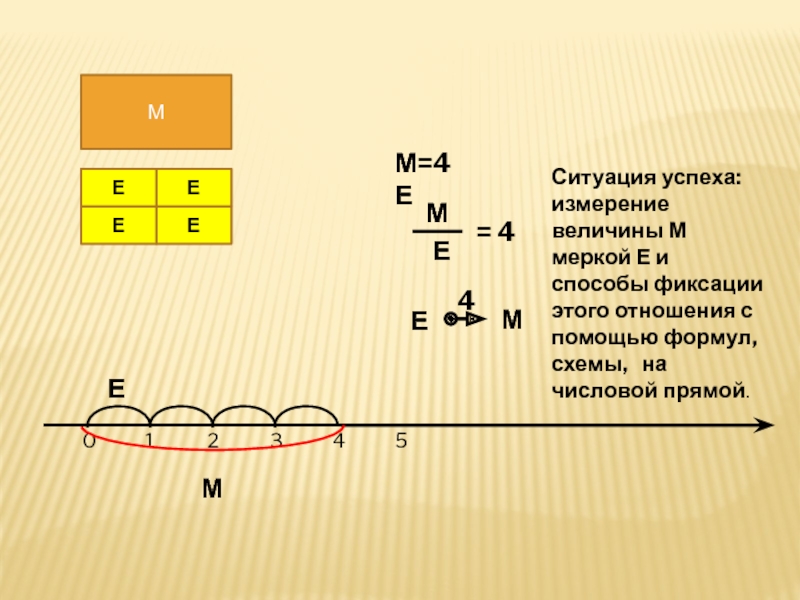
- 6. МЕЕЕЕМ=4Е= 4Е4ММЕМ012345ЕМСитуация успеха: измерение величины М меркой
- 7. М=4Е= числоМЕвеличинаединица= 4Е4Мвеличинаединицачисловеличина=число.единицаДанная таблица получается после обсуждения в группах
- 8. МВопрос: Что это за число?
- 9. ЕЕСМСМ535 3промежуточная мерка2 класс. Новый
- 10. Построить фигуры с площадями М и В,
- 11. Сравнение двух способов измерения величины с помощью
- 12. Единицу Е разбиваем на р равных частей
- 13. М ? К
- 14. 5 класс Обыкновенные дроби Измерить величину М меркой ЕМЕМЕС32⅔C
- 15. 2 класс Тема: позиционные системы счисленияМЕВеличина,
- 16. ЕЕ1Е 2Е1ЕЕ 233Система мерок в троичной системе1Е2 + 2Е1 + 1ЕММ = 121(3)ЕМ =2 класс5 класс
- 17. 5 класс СТАНДАРТНЫЙ СПОСОБ ЗАПИСИ МНОГОЗНАЧНОГО
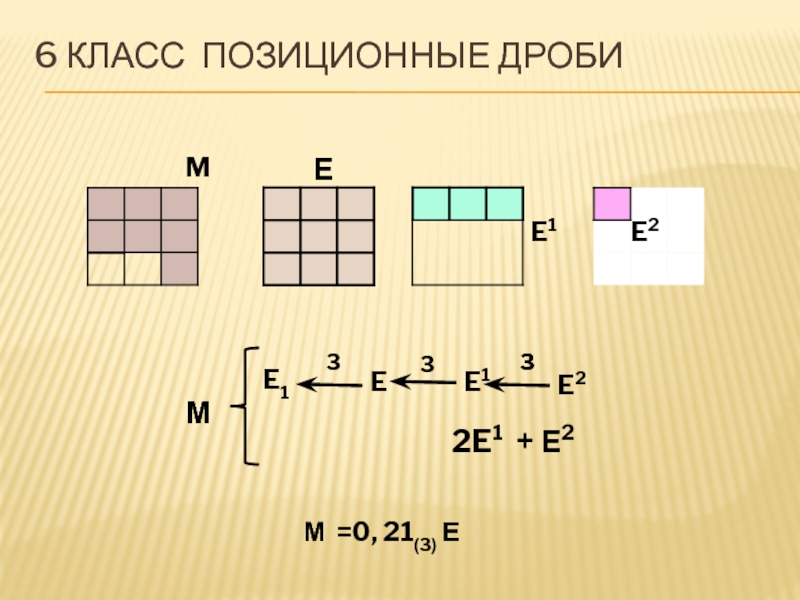
- 18. ME1E2E2E1E3333E1 2E1 + Е2ММ =0, 21(3) Е6 класс позиционные дроби Е
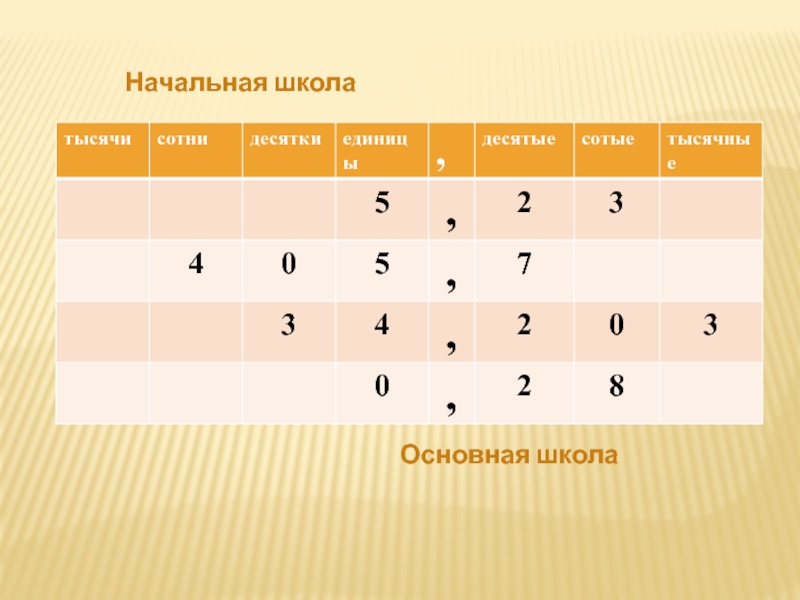
- 19. Начальная школаОсновная школа
- 20. 6 класс Положительные и отрицательные числа
- 21. Опыт работы по системе Д.Б.Эльконина-В.В.Давыдова в начальной
- 22. Литература
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Развитие понятия числа
(система Д.Б.Эльконина – В.В. Давыдова)
Гаврюшина Л.С.,
учитель
математики МБОУ СОШ №12
Слайд 2В основе курса обучения математике по системе Д.Б.Эльконина-В.В.Давыдова положена концепция
действительного числа. В отличие от обычной программы предусмотрен такой вводный
раздел, при усвоении которого дети специально изучают исходное основание последовательного выведения всех видов действительного числа, а именно изучают понятие величины. Преемственность в обучении требует уже в начальной школе рассматривать основное математическое понятие - понятие числа через понятие величины. Операцией, специфической для способа измерения величин, является «откладывание» единицы измерения (мерки) на измеряемой величине и счет таких откладываний. Число в этом случае является характеристикой величины и зависит не только от измеряемой величины, но и от выбранной мерки. Меняя условия, при которых с помощью практических действий решается задача измерения и обратная ей задача построения (воспроизведения) величины посредством «откладывания» мерок (единиц измерения), дети будут «выращивать» различные виды чисел, знакомясь с общепринятыми способами их обозначений.Слайд 4Выполнив практическое задание, учащиеся получают ответ: мерка Е укладывается в
величине М 3 раза
М
Е
3
М
Слайд 6М
Е
Е
Е
Е
М=4Е
= 4
Е
4
М
М
Е
М
0
1
2
3
4
5
Е
М
Ситуация успеха: измерение величины М меркой Е и способы
фиксации этого отношения с помощью формул, схемы, на числовой
прямой.Слайд 7М=4Е
= число
М
Е
величина
единица
= 4
Е
4
М
величина
единица
число
величина
=
число
.
единица
Данная таблица получается после обсуждения в группах
Слайд 8М
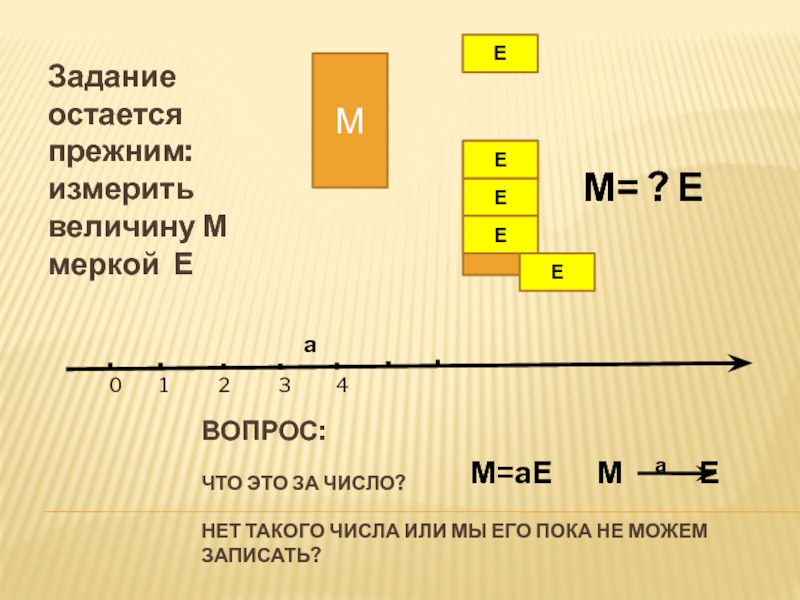
Вопрос:
Что это за число?
Нет такого числа или мы
его пока не можем записать?
Задание остается прежним: измерить величину М
меркой ЕМ
Е
Е
Е
Е
Е
М= ? Е
М=aЕ М a Е
0
1
3
4
2
a
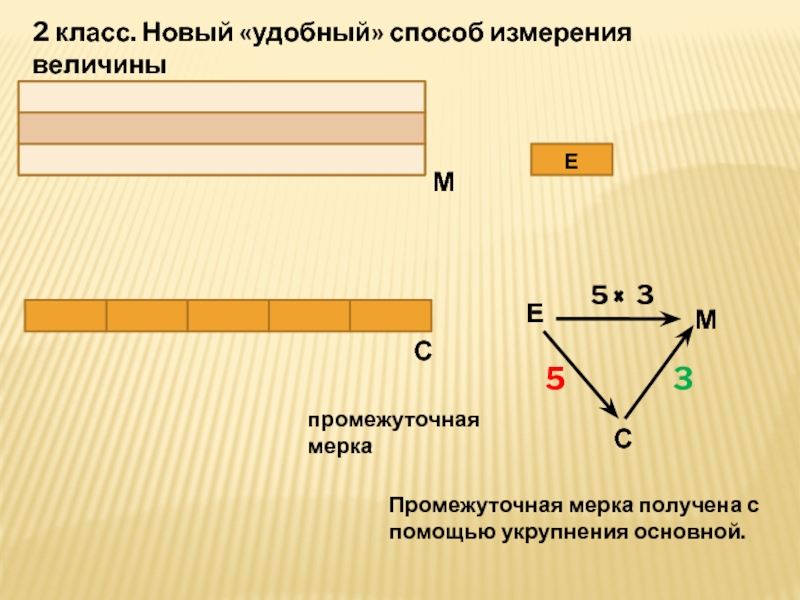
Слайд 9Е
Е
С
М
С
М
5
3
5 3
промежуточная мерка
2 класс. Новый «удобный» способ измерения
величины
Промежуточная мерка получена с помощью укрупнения основной.
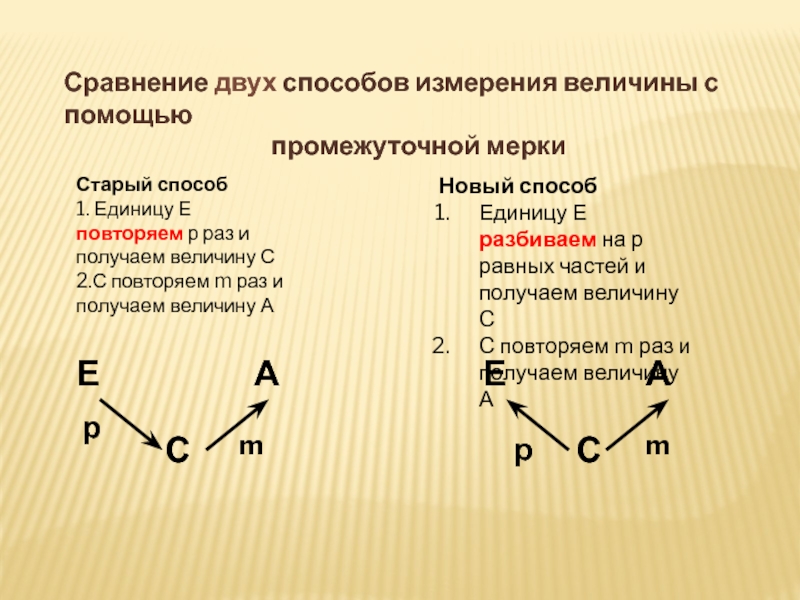
Слайд 11Сравнение двух способов измерения величины с помощью
промежуточной мерки
Старый способ
1.
Единицу Е повторяем р раз и получаем величину С
2.С повторяем
m раз и получаем величину АНовый способ
Единицу Е разбиваем на р равных частей и получаем величину С
С повторяем m раз и получаем величину А
Е А
С
Е А
С
р
р
m
m
Слайд 12Единицу Е разбиваем на р равных частей и получаем величину
С
С повторяем m раз и получаем величину М
Е
М С
В
p
m
p
m
1. Единицу Е повторяем m раз и получаем величину B
2.B разбиваем на p равных частей и получаем величину М
?
Гипотеза о перестановочности в новом способе
m/p
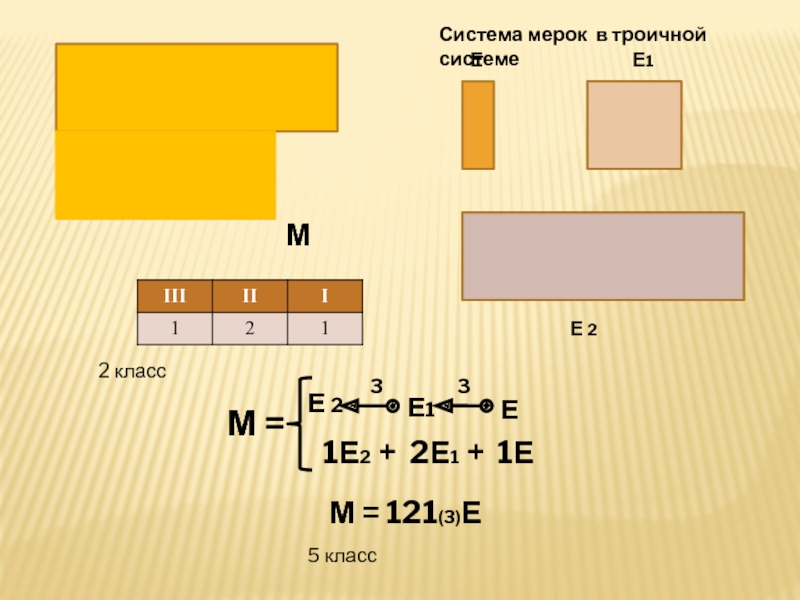
Слайд 152 класс
Тема: позиционные системы счисления
М
Е
Величина, которую надо измерить, намного
больше данной мерки. У учащихся возникает потребность в новом способе
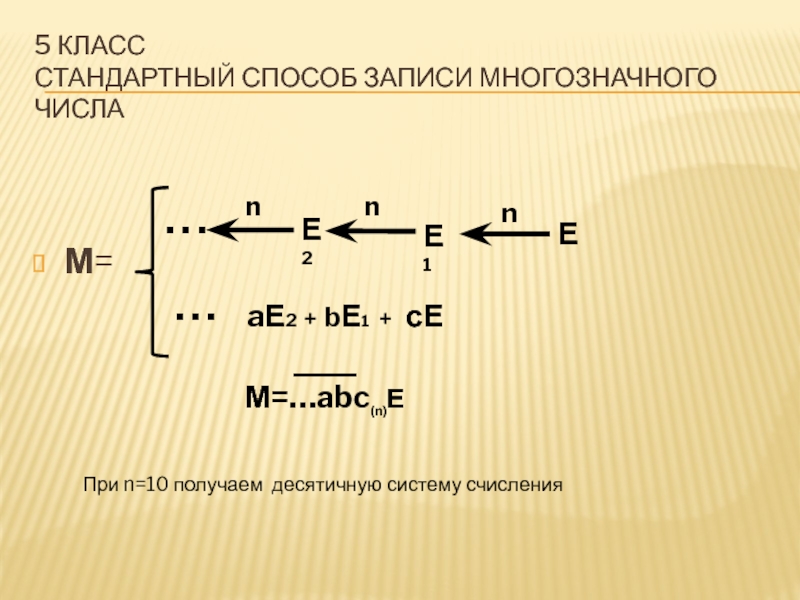
действия: использование набора мерок и записи результата измерения в таблицу.Слайд 175 класс
СТАНДАРТНЫЙ СПОСОБ ЗАПИСИ МНОГОЗНАЧНОГО ЧИСЛА
М=
Е
Е1
Е2
…
n
n
n
…
aЕ2 +
bЕ1 + сЕ
М=…abc(n)Е
При n=10 получаем десятичную систему счисления
Слайд 21Опыт работы по системе Д.Б.Эльконина-В.В.Давыдова в начальной школе и основной
показывает, что обучающиеся по этой программе, отличаются тем, что могут
конструировать разные виды чисел и употреблять различные модели как средства разрешения учебных и математических проблем;
решать круг практических задач, выходя за пределы применимости открытых учащимися способов действия, т.е. решать задачи в новых условиях,
освоить вычислительные навыки и способы решения задач за более короткий отрезок времени.
Слайд 22
Литература
1.В.В.Давыдов
. Теория развивающего обучения.- М."Интор",1996. 2. В.В. Репкин, Н.В.Репкина.Развивающее обучение:
теория и практика.- Томск, "Пеленг", 1997. 3. В.П.Зинченко. Психологические основы педагогики. М."Гардарики",2002. 4. А.Б.Воронцов ,Е.В.Чудинова. Психолого-педагогические основы развивающего обучения. М.,2003. 5. А.Б.Воронцов Педагогическая технология контроля и оценки учебной деятельности. М."РассказовЪ",2002. 6. Г.А.Цукерман Виды общения в обучении. Томск, "Пеленг, 1994. 7. Г.А.Цукерман Оценка без отметки. – Рига, 1999. 8. Г.А.Цукерман Как младшие школьники учатся учиться.-Рига, 2000.9. В.В.Давыдов, С.Ф.Горбов, Г.Г.Микулина, О.В.Савельева. Математика. Учебники для 1-4 класс. М., Вита-пресс, 2010
10.С.Ф.Горбов, В.М.Заславский, А.В.Морозова, Н.Л.Табачникова. Математика. Учебник-тетрадь 5 класс . М., Вита-пресс, 2005
11.С.Ф.Горбов, В.М.Заславский, О.А.Захарова, А.В.Морозова, Н.Л.Табачникова. Учебно-методический комплект « Математика. 6 класс» . М., Вита-пресс, 2006
12.С.Ф.Горбов, В.М.Заславский, А.В.Морозова, Н.Л.Табачникова. Обучение математике. 5 класс . Пособие для учителя. М., Вита-пресс, 2006