Задачи о среднем арифметическом и медиане

Задачи с решениями
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

КОЛЛЕДЖ СВЯЗИ № 54 имени П.М. ВОСТРУХИНА

Разработчик:
Преподаватель математики
Т.Н. Рудзина

медиану, то есть задачи, где ничего считать не надо, а

требуется только четко знать определение соответствующей характеристики.

Добавляет сложности и часто несколько запутанное условие.

Задача 1. Средний рост ученика в классе составляет 171см (то есть среднее арифметическое значений роста для всех учеников класса равно 171 см). Известно, что в классе учатся Вася Васин, чей рост равен 180см. Выберите верное утверждение:
А. В классе есть ученик ростом 162 см.
Б. В классе есть ученик ростом ровно 171 см.
В. В классе есть ученик ростом менее 171 см.
Г. Вася Васин – самый высокий ученик класса

Есть четыре группы кандидаток в стюардессы: А, Б, В, Г.

В какой из них, по крайней мере, половина девушек, может работать стюардессами, если выполнены следующие условия:
А – рост самой высокой девушки равен 185 см;
Б – средний рост девушек равен 171 см;
В – рост самой невысокой девушки 168 см;
Г – медиана роста девушек равна 170,5 см.

В таблице показано время (в минутах), которое тратит Петя на

дорогу из школы домой каждый день в течении недели. Найдите среднее время, которое он тратит каждый день на дорогу из школы домой.

и среднее арифметическое не один, а два или более раза.

Петя и Паша на дорогу из школы домой каждый день

в течении недели.
Найти, кто из мальчиков в среднем тратил больше времени на дорогу, и на сколько минут.

по математике: 2,3,3, 2, 2, 2, 2, 5, 2, 5.

Найдите, насколько отличается медиана его оценок от его среднего балла.

среднее и многие другие «средние» призваны показывать некоторое «характерное», «типичное»

значение варианты для данной выборки. Как мы видели в различных задачах, значение этих характеристик могут отличаться друг от друга, притом значительно. Обычно, когда в задачах говориться о среднем значении какой-то величины, имеется в виду именно среднее арифметическое значение этой величины. Как правило, более разумно «характеризующей» данную выборку величиной является среднее арифметическое, однако, это не всегда так.

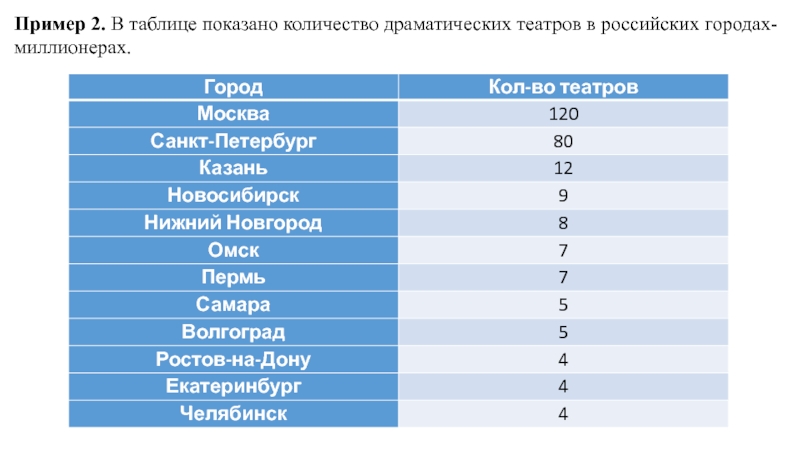
В некоторых случаях медиана является более адекватной оценкой. Это происходит в тех случаях, когда данные содержат так называемые выбросы, то есть отдельные значения вариант, резко отличающиеся от остальных, например, в большую сторону. Эти выбросы заметно влияют на среднее арифметическое, а на медиану вследствие своей малочисленности влияние практически не оказывают.

городах-миллионерах.

оценивания.
В классе Ильи годовые оценки по геометрии – следующие:
8,

5, 4, 10, 4, 4, 4, 5, 4, 10, 4, 4, 6, 4, 4.
Найдите медиану, моду и среднее арифметическое этого набора оценок.
Какая из этих характеристик, на Ваш взгляд, лучше отражает среднюю оценку по геометрии в этом классе?
Ответ обоснуйте.