{ ЛЕКЦИЯ 4 } { Алгоритмы сортировки и поиска }

R1, R2,… RN. Каждый элемент характеризуется некоторой информацией и ключом

K1. На множестве ключей определены операции сравнения: «>», «<» и т.д.
Задачей сортировки является нахождение такой перестановки ключей p1, p2,… pN, после которой ключи расположились бы в заданном порядке:
неубывания
невозрастания


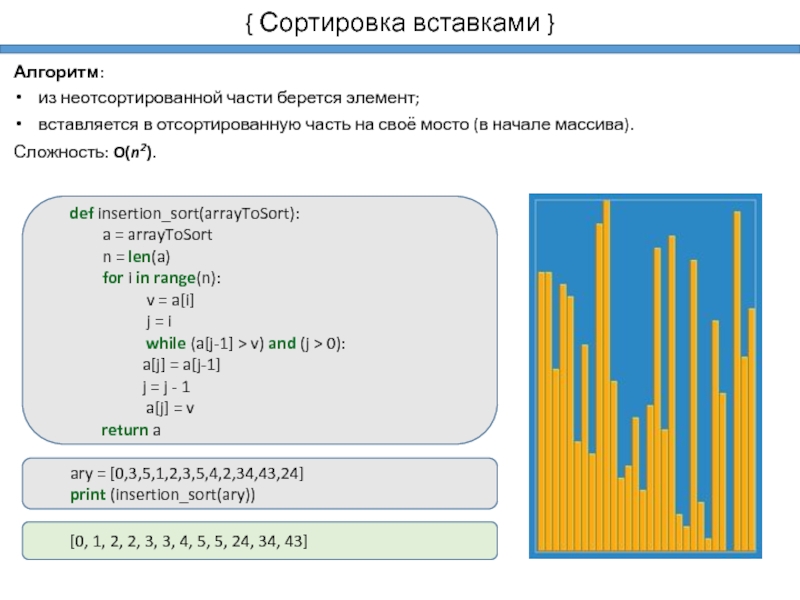
Для классификации алгоритмов сортировки используются:
сложность;
потребности в дополнительной памяти;
области хранения данных (внутренняя (в ОЗУ) и внешняя сортировка (вне ОЗУ));
свойство устойчивые (меняется ли положение элементов с одинаковыми ключами);
наличие в алгоритме операции сравнения.

сортировки.
Возможно, самый неэффективный алгоритм.
Сложность: O(n*n!).
(Колода в 32 карты будет сортироваться

компьютером в среднем 2,7⋅1019 лет.)

его в начало;
сдвинуть начало неотсортированной части.
Сложность: O(n2).

часть на своё мосто (в начале массива).
Сложность: O(n2).

за другом;
в случае несоответствия выбранному порядку меняются местами.
Сложность: O(n2).

за другом;
в случае несоответствия выбранному порядку меняются местами.
Сложность: O(n2).

одинакового размера;
Каждая из получившихся частей сортируется отдельно, например — тем

же самым алгоритмом;
Два упорядоченных массива половинного размера соединяются в один.
Сложность: O(n log2 n).

одинакового размера;
Каждая из получившихся частей сортируется отдельно, например — тем

же самым алгоритмом;
Два упорядоченных массива половинного размера соединяются в один.
Сложность: O(n log2 n).

одинакового размера;
Каждая из получившихся частей сортируется отдельно, например — тем

же самым алгоритмом;
Два упорядоченных массива половинного размера соединяются в один.
Сложность: O(n log2 n).

прямого обмена («Пузырьковая сортировка»), весьма низкой эффективности. Принципиальное отличие состоит

в том, что в первую очередь производятся перестановки на наибольшем возможном расстоянии и после каждого прохода элементы делятся на две независимые группы.
Таким образом, улучшение неэффективного прямого метода сортировки дало один из наиболее эффективных методов.
Алгоритм:
выбрать (опорным) элемент из массива;
перераспределить элементы в массиве так, что элементы меньше опорного помещаются перед ним, а больше или равные после;
применить первые два шага к подмассивам слева и справа от опорных элементов, пока в подмассивах не останется не более одного элемента.
Сложность: Средняя O(n log2 n), Худшая O(n2).

Худший случай.
Если каждое разделение даёт два подмассива размерами 1 и n-1, т.е. при каждом разбиении больший массив будет укорачиваться на 1. Это может произойти, если за опорный будет выбраться либо наименьший, либо наибольший элемент из всех обрабатываемых.
При выборе опорного элемента — первого или последнего в массиве, — такой эффект даст уже отсортированный массив.

v, i, j = a[r], l -

1, r

while (True):
i, j = i + 1, j - 1
while(a[i] < v): i = i + 1
while(a[j] > v): j = j - 1
if (i >= j): break
a[i], a[j] = a[j], a[i]

a[i], a[r] = a[r], a[i]

quicksort(a, l, i - 1)
quicksort(a, i + 1, r)

величине элемент массива:
максимальный (минимальный) элемент массива: 1-ая (N-ая) порядковая статистика;
медиана

– «средний» по величине элемент, примерно половина элементов не больше, примерно половина элементов не больше, примерно половина – не меньше.
Алгоритм нахождения k-й порядковой статистики методом «разделяй и властвуй»:
выберем случайным образом элемент v массива S;
разобьём массив на три: Sl, элементы которого меньше, чем v; Sv, элементы которого равны v, и Sr, элементы которого больше, чем v;
введём функцию Selection(S, k), где S — массив, а k — номер порядковой статистики:

R1, R2,… RN. Каждый элемент характеризуется некоторой информацией и ключом

Ki. На множестве ключей определены операции сравнения: «>», «<» и т.д.
Задачей поиска является нахождение индекса ключа, совпадающего со значением key.

Алгоритмы поиска:
линейный, последовательный поиск (неотсортированный массив);
поиск сужением зоны (отсортированный массив).

Выбором структуры данных (устройством хранимой информации) можно расставить приоритеты:
быстрое и простое изменение данных;
Быстрый поиск.

корня.

Корни нелинейного уравнения.
Пусть дана некоторая функция f(x) и требуется найти

значения x, для которых

Определение. Значение x*, при котором f(x*) = 0, называется корнем (или решением) уравнения.
Геометрически корень уравнения есть точка пересечения графика функции y = f(x) с осью абсцисс.
На графике изображены три корня:


При этом они отличаются


Корни типа называются простыми, а . – кратными (непростыми).
Большинство методов решения уравнений ориентировано на отыскание простых корней.

корня.

Двухточечные методы (уменьшение отрезка локализации).
Методы выбора точки с:
Метод половинного

деления (метод дихотомии)


Метод золотого сечения



Метод хорд

для сортировки итерируемых объектов и метод list.sort() для сортировки списка

с заменой исходного.
Сделать обычную сортировку по возрастанию просто — достаточно вызвать функцию sorted(), которая вернёт новый отсортированный список:







У list.sort() и sorted() есть параметр key для указания функции, которая будет вызываться на каждом элементе до сравнения. Значение параметра key должно быть функцией, принимающей один аргумент и возвращающей ключ для сортировки.