Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы и действия над ними.ppt
Содержание
- 1. Матрицы и действия над ними.ppt
- 2. ПЛАН ЛЕКЦИИ 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ2.
- 3. ПОНЯТИЕ И ВИДЫ МАТРИЦ
- 4. ОПРЕДЕЛЕНИЯ МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ
- 5. ВИДЫ МАТРИЦ
- 6. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ
- 7. ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВСТРОКИ НУМЕРУЮТСЯ
- 8. СТРОКА И СТОЛБЕЦ
- 9. РАЗМЕР МАТРИЦЫМАТРИЦА, ИМЕЮЩАЯ m СТРОК И n СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙРАЗМЕРА m НА n.
- 10. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
- 11. ЭЛЕМЕНТ МАТРИЦЫ
- 12. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
- 13. ТРЕУГОЛЬНЫЕ МАТРИЦЫ
- 14. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 15. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
- 16. МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
- 17. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
- 18. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
- 19. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
- 20. ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ
- 21. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ
- 22. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
- 23. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
- 24. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
- 25. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
- 26. § 1. Матрицы и действия над ними1.
- 27. Две матрицы A и B считаются равными,
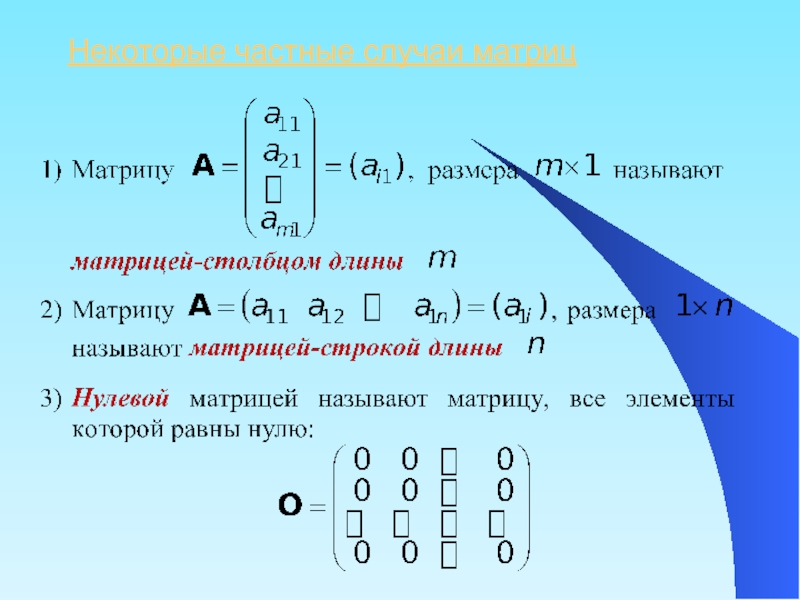
- 28. Некоторые частные случаи матриц
- 29. Элементы a11, a22, …, akk (где k
- 30. 5) Пусть A = (aij) – квадратная
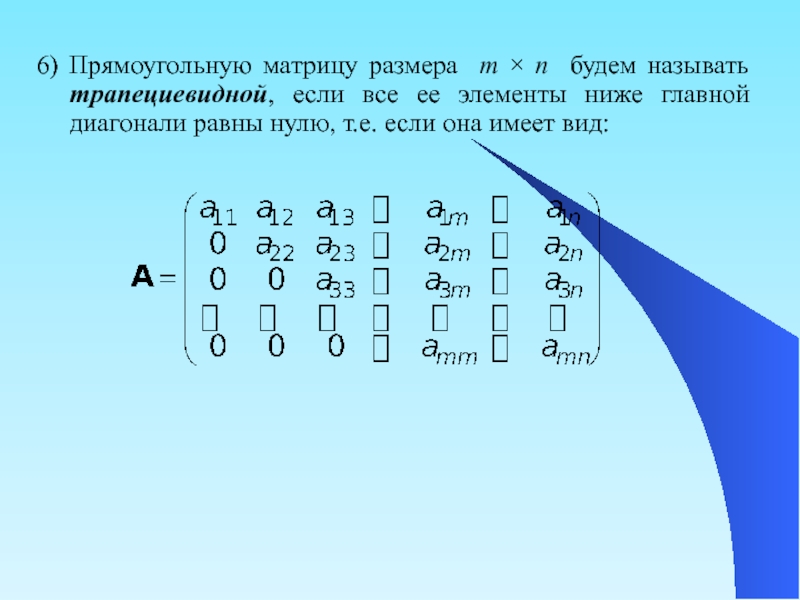
- 31. 6) Прямоугольную матрицу размера m × n
- 32. 2. Линейные операции над матрицами 1) Умножение
- 33. ОПРЕДЕЛЕНИЕ. Суммой двух матриц A=(aij) и B=(bij)
- 34. Свойства линейных операции над матрицами
- 35. 3. Нелинейные операции над матрицами 1) Умножение
- 36. ОПРЕДЕЛЕНИЕ. Пусть A=(aij) – матрица размера m
- 37. Свойства операции умножения матриц
- 38. ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m
- 39. ПримерОтветназад
- 40. Матрица, полученная из данной заменой каждой ее
- 41. В случае, когда АВ=ВА, матрицы А и
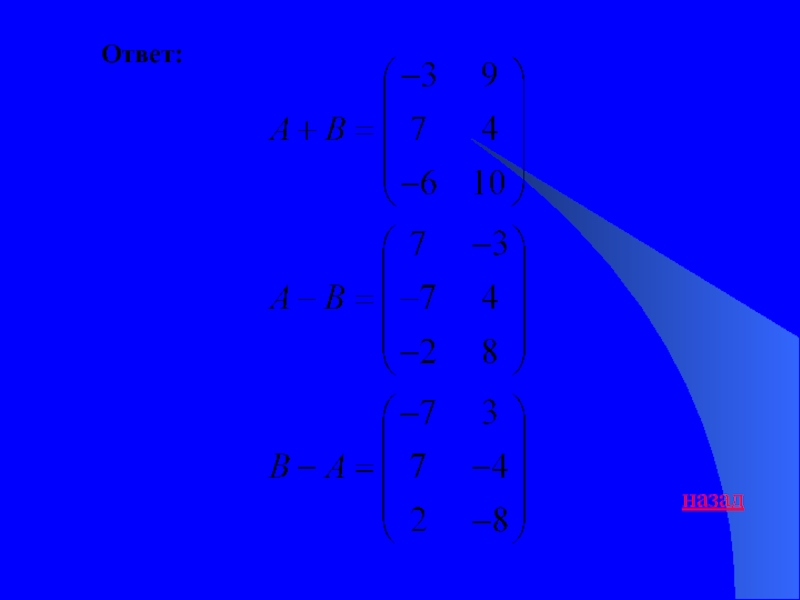
- 42. Ответ:назад
- 43. ПримерОтветназад
- 44. Ответ:назад
- 45. ПримерОтветназад
- 46. Ответ:назад
- 47. Ответ: илиилиназад
- 48. Скачать презентанцию
ПЛАН ЛЕКЦИИ 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦ 3. ОПЕРАЦИИ НАД МАТРИЦАМИ
Слайды и текст этой презентации
Слайд 4 ОПРЕДЕЛЕНИЯ
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА,
ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.
Слайд 7ПРИНЦИП НУМЕРАЦИИ
СТРОК И СТОЛБЦОВ
СТРОКИ НУМЕРУЮТСЯ СВЕРХУ
ВНИЗ, НАЧИНАЯ С
№ 1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
Слайд 20ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ
МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА,
МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО
ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ BСлайд 21 ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО
УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
Слайд 26§ 1. Матрицы и действия над ними
1. Определение и некоторые
виды матриц
ОПРЕДЕЛЕНИЕ. Матрицей размера m×n называется таблица, образованная из элементов
некоторого множества (например, чисел или функций) и имеющая m строк и n столбцов. Если m ≠ n, то матрицу называют прямоугольной.
Если m = n, то матрицу называют квадратной, порядка n.
Элементы, из которых составлена матрица, называются элементами матрицы.
Например, a24 –
a13 –
Слайд 27Две матрицы A и B считаются равными, если они одинакового
размера, и элементы, стоящие в A и B на одинаковых
местах, равны между собой, т.е. aij = bij.Слайд 29Элементы a11, a22, …, akk (где k = min{m,n}) будем
называть элементами главной диагонали матрицы.
Квадратная матрица, у которой все элементы,
стоящие вне главной диагонали, равны нулю, называется диагональной: Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной:
Обозначают: E или En.
Слайд 305) Пусть A = (aij) – квадратная матрица порядка n.
Элементы a1n, a2,n-1, a3,n-2, …, an1 будем называть элементами побочной
диагонали матрицы.Квадратные матрицы, у которых все элементы ниже (выше) главной или побочной диагонали равны нулю, называются треугольными :
Слайд 316) Прямоугольную матрицу размера m × n будем называть трапециевидной,
если все ее элементы ниже главной диагонали равны нулю, т.е.
если она имеет вид:Слайд 322. Линейные операции над матрицами
1) Умножение матрицы на число;
2)
Сложение матриц.
ОПРЕДЕЛЕНИЕ. Произведением матрицы A=(aij) на число α называется такая
матрица B=(bij), элементы которой равны произведениям соответствующих элементов матрицы A на число α, т.е. bij= α·aij.Обозначают: α·A, αA.
Частный случай: (-1)·A – противоположная матрице A,
Обозначают –A.
Слайд 33ОПРЕДЕЛЕНИЕ. Суммой двух матриц A=(aij) и B=(bij) одинакового размера, называется
такая матрица C=(cij), элементы которой равны суммам соответствующих элементов
матриц A и B, т.е. cij = aij + bij .Обозначают: A+B
Частный случай: A+(–B) – разность матриц A и B.
Обозначают: A–B
Слайд 353. Нелинейные операции над матрицами
1) Умножение двух матриц;
2) Транспонирование
матрицы.
ОПРЕДЕЛЕНИЕ. Пусть A=(a1i) и B=(bi1) – матрица-строка и матрица-столбец одинаковой
длины n. Произведением матрицы-строки A на матрицу-столбец B называется число c, равное сумме произведений их соответствующих элементов, т.е. c = a11 · b11 + a12 · b21 + a13 · b31 + … + a1n · bn1 .
Слайд 36ОПРЕДЕЛЕНИЕ. Пусть A=(aij) – матрица размера m × n, B=(bij)
– матрица размера n × k (т.е. количество столбцов в
матрице A совпадает с количеством строк матрицы B). Произведением матрицы A на матрицу B называется матрица C =(cij) размера m × k такая, что каждый ее элемент cij является произведением i-й строки матрицы A на j-й столбец матрицы B, т.е.cij = ai1 · b1j + ai2 · b2j + ai3 · b3j + … + ain · bnj .
Обозначают: A ·B, AB.
Слайд 38ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m × n. Матрица
размера n × m, полученная из A заменой каждой ее
строки столбцом с тем же номером, называется транспонированной к A и обозначается AТ.Операция нахождения матрицы AТ называется транспонированием матрицы A.
Свойства операции транспонирования матриц
1) (AТ )T = A ;
2) (A + B)T = AT + BT ;
3) (αA)T = αAT ;
4) (A · B)T = BT · AT .
Слайд 40Матрица, полученная из данной заменой каждой ее строки столбцом с
тем же номером, называется матрицей, транспонированной относительно данной.
Например:
Свойства
назад
Слайд 41В случае, когда АВ=ВА, матрицы А и В называют перестановочными
или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
Пример 2.
Найти все перестановочные матрицы к матриценазад