Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Lec1.ppt
Содержание
- 1. Lec1.ppt
- 2. ЛЕКЦИЯ 1 .ЭЛЕКТРОННАЯ ВЕТВЬ ВОЗБУЖДЕНИЯ В КРИСТАЛЛАХ.
- 3. Разложение функции в ряд Фурье В силу
- 4. “Операторность” заключена
- 5. Система металла (как и любая устойчивая макроскопическая
- 6. В этой формуле последние три слагаемые- некулоновские
- 7. ; ; Таким образом, выражение в фигурных скобках равно
- 8. ПолучаемОстался вклад только от одной ячейки (в
- 9. (!) отвечает бесконечная длина волны;
- 10. Для плоского (двумерного) кристалла первый член уже
- 11. Ионная решетка, погруженная в электронную жидкость. Эта
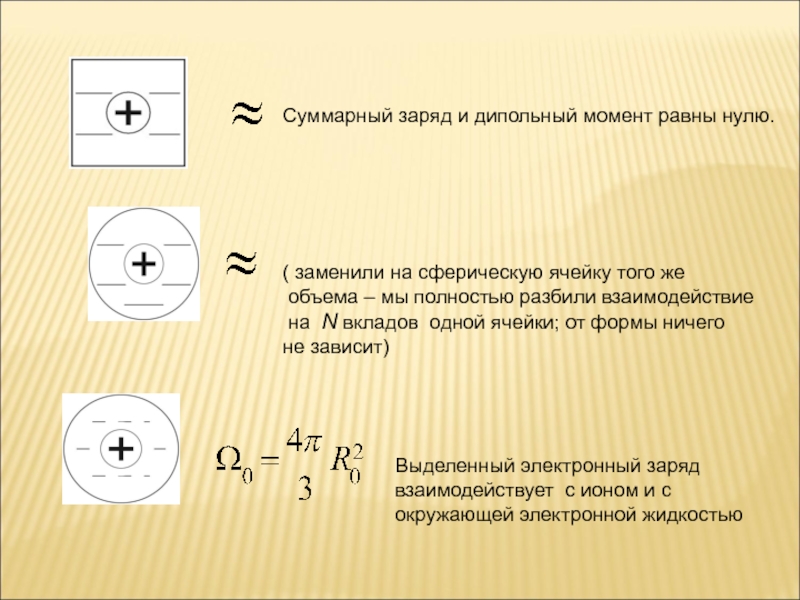
- 12. Суммарный заряд и дипольный момент равны нулю. (
- 13. Интегрируем по всей ячейке.(При расчете считаем ,
- 14. Энергия системы оказалась отрицательной. Таким образом, система с полностью скомпенсированным (погашенным) зарядом устойчива.
- 15. Скачать презентанцию
ЛЕКЦИЯ 1 .ЭЛЕКТРОННАЯ ВЕТВЬ ВОЗБУЖДЕНИЯ В КРИСТАЛЛАХ. ПЛАЗМЕННАЯ МОДЕЛЬ НЕПЕРЕХОДНОГО МЕТАЛЛА. ГАМИЛЬТОНИАН ЭЛЕКТРОН-ИОННОЙ СИСТЕМЫ. УСЛОВИЕ ГЛОБАЛЬНОЙ И ЛОКАЛЬНОЙ ЭЛЕКТРОНЕЙТРАЛЬНОСТИ.Гамильтониан системы, Ионы тяжелые, их кин. энергию учитывать не будемКинетическая энергия электронов Энергия
Слайды и текст этой презентации
Слайд 2ЛЕКЦИЯ 1 .ЭЛЕКТРОННАЯ ВЕТВЬ ВОЗБУЖДЕНИЯ В КРИСТАЛЛАХ. ПЛАЗМЕННАЯ МОДЕЛЬ НЕПЕРЕХОДНОГО
МЕТАЛЛА. ГАМИЛЬТОНИАН ЭЛЕКТРОН-ИОННОЙ СИСТЕМЫ. УСЛОВИЕ ГЛОБАЛЬНОЙ И ЛОКАЛЬНОЙ ЭЛЕКТРОНЕЙТРАЛЬНОСТИ.
Гамильтониан системы
,
Ионы тяжелые, их кин. энергию учитывать не будем
Кинетическая энергия электронов
Энергия электрон – электронного
взаимодействия
Слайд 3Разложение функции в ряд Фурье
В силу полноты набора экспоненциальных
функций типа плоских волн
любую функцию можно разложить в ряд
Фурье.Оператор электрон-
электронного
взаимодействия
Слайд 4“Операторность” заключена в координатах электронов.
Вклад
дают обратному расстоянию между частицами
Слайд 5Система металла (как и любая устойчивая макроскопическая
система в целом
электронейтральна. Электроны могут
(в принципе) собраться все в одной части
металла, тогда она будет заряжена отрицательно, а кусок (область) , где
электронов нет – положительно. Конечно, в реальности такого
никогда не происходит. Чтобы избежать этой возможности
при описании, потребуем локальной электронейтральности
(чтобы нейтральными был любой, даже быть может,
микроскопически малый объем).
--среднее значение
Слайд 6В этой формуле последние три слагаемые- некулоновские члены;
первый член
самый главный:
расстояния большие -это кулоновское взаимодействие (конкретный вид).
Слайд 8Получаем
Остался вклад только от одной ячейки (в первом слагаемом),
второе
слагаемое содержит
.
Первое слагаемое
Второе слагаемое
- макроскопическое число. 
Слайд 9
(!)
отвечает бесконечная длина волны;
максимальная длина волны
равна размеру кристалла
.
(всего ячеек
– линейный размер)Второе слагаемое всегда >> первого в
раз.
Слайд 10Для плоского (двумерного) кристалла первый член уже нельзя было бы
выкинуть , следовательно, условие
локальной электронейтральностисистем пониженной размерности требует отдельного рассмотрения.
Таким образом, с макроскопической точностью,
Мы использовали трехмерность системы.
Таким образом, с макроскопической точностью,
Слайд 11Ионная решетка, погруженная в электронную жидкость.
Эта система чисто вспомогательная;
мы предполагаем,
что - жидкость остается неоднородной,
несмотря на присутствие
ионов.
Слайд 12Суммарный заряд и дипольный момент равны нулю.
( заменили на сферическую
ячейку того же
объема – мы полностью разбили взаимодействие
на
N вкладов одной ячейки; от формы ничего не зависит)
Выделенный электронный заряд взаимодействует с ионом и с окружающей электронной жидкостью
Слайд 13Интегрируем по всей ячейке.
(При расчете считаем , что ионы точечные!
)
Для вспомогательных электронов не надо учитывать неточечность. Этот электронный
заряд взаимодействует также и с остальными электронами из сферы. По теореме Гаусса, заряд, распределенный по сфере, эквивалентен точечному заряду в центре;
Слайд 14
Энергия системы оказалась отрицательной. Таким образом, система с
полностью скомпенсированным
(погашенным) зарядом устойчива.
