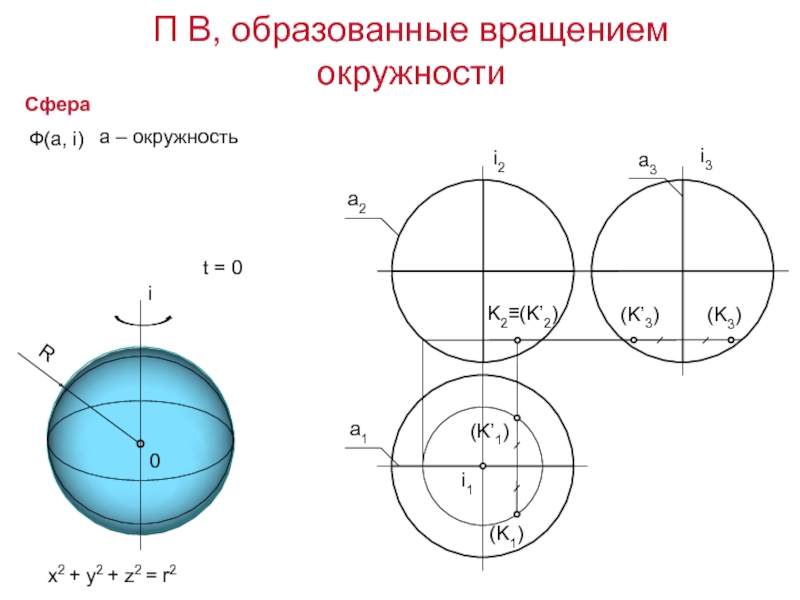
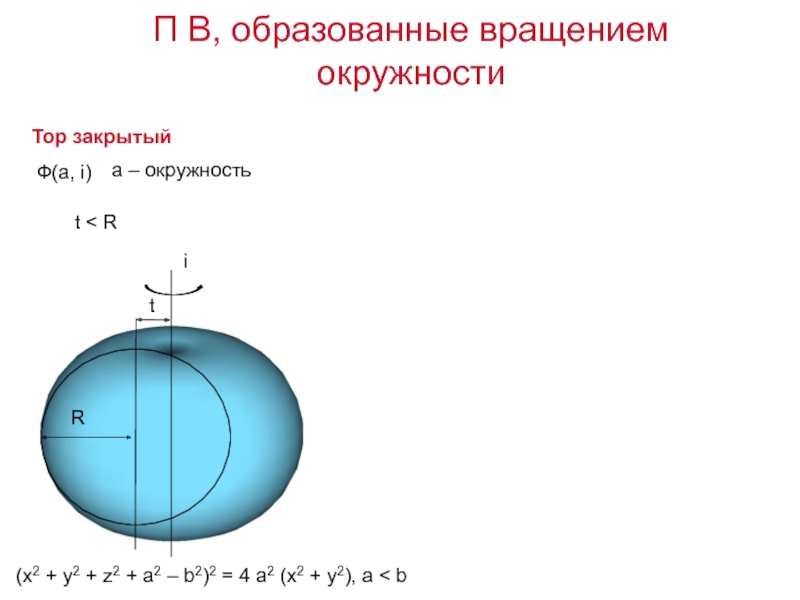
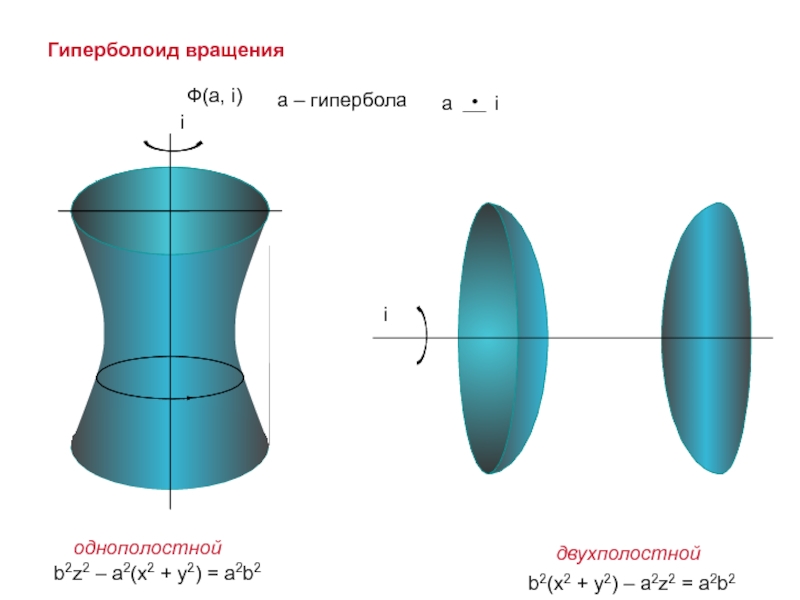
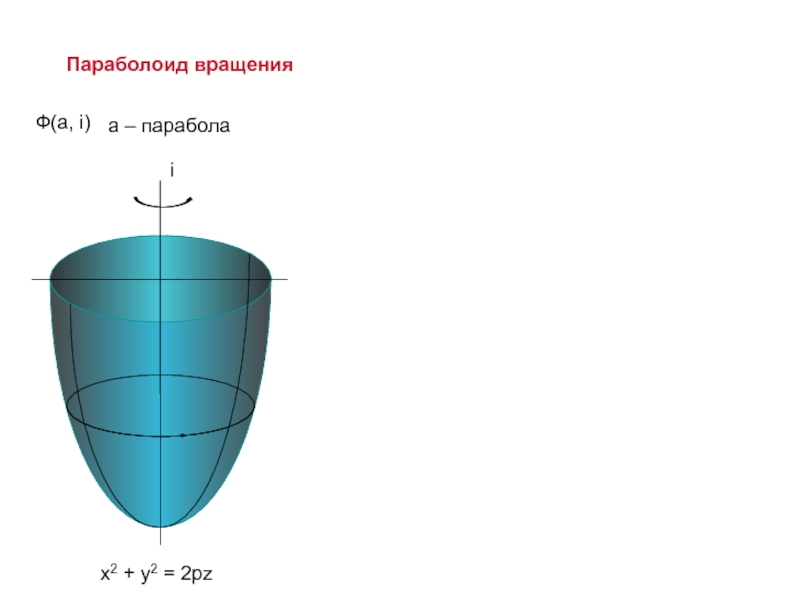
линии a, перемещающейся в пространстве по определенному закону.
Закон перемещения линии
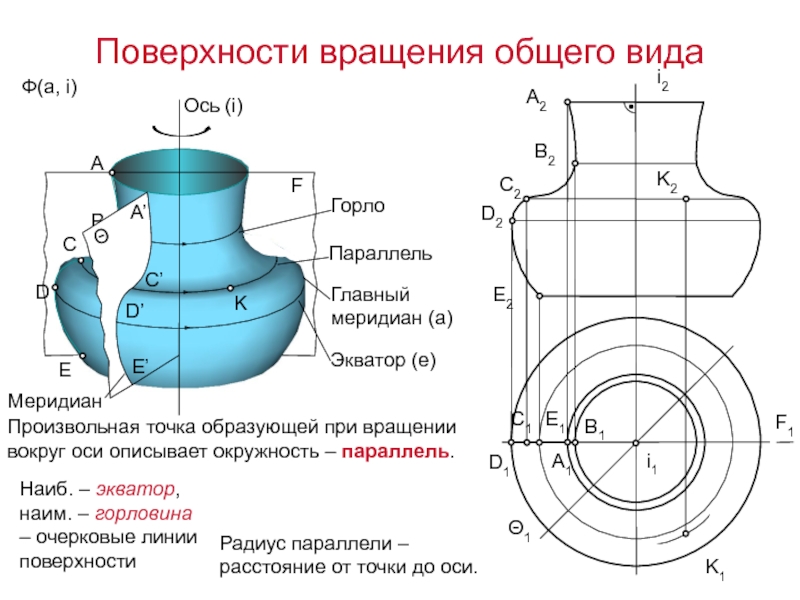
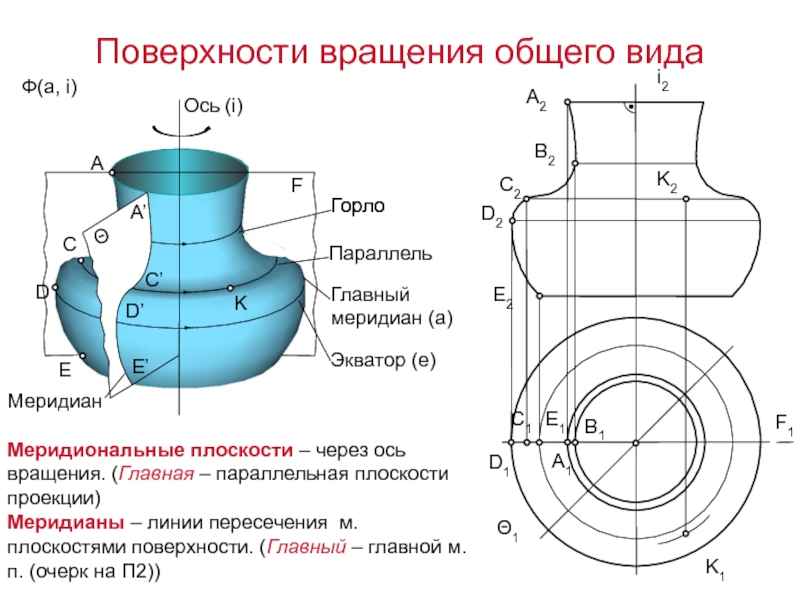
а целесообразно задать в виде семейства линий m, n. Подвижная линия а называется образующей, неподвижные линии m, n – направляющими.
m
n
a''
a
a'




![5.Поверхности_кор.ppt Линейчатые развёртываемые поверхности Цилиндрические поверхности Ф(a, m, s) [a ∩ m, Линейчатые развёртываемые поверхности Цилиндрические поверхности Ф(a, m, s) [a ∩ m, a II s],](/img/thumbs/44b3224f144e873b1e78d171516e4e65-800x.jpg)
![5.Поверхности_кор.ppt Призматические поверхности Ф(a, m, s) [a ∩ m, a II s] m-ломаная линия s-направляющий вектор asma'a'''a'' Призматические поверхности Ф(a, m, s) [a ∩ m, a II s] m-ломаная линия s-направляющий вектор](/img/thumbs/f822b4e2f25252754deb15ec2e0c696e-800x.jpg)
![5.Поверхности_кор.ppt Пирамидальные поверхности Sama'a''a'''Ф(a, m, S) [a∩m, S∈ a] Пирамидальные поверхности Sama'a''a'''Ф(a,](/img/thumbs/1d00c4a6be1a0b66c513cdde87023fc5-800x.jpg)