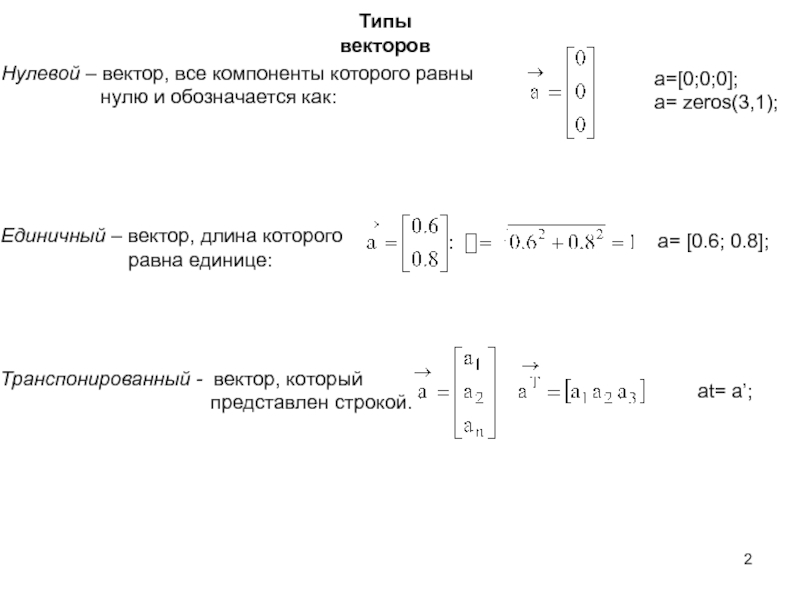
вектора в n-мерном пространстве и обозначить как:
или понятие точки
A(a1,a2,a3,…,an). Числа a1,a2,a3,…,an называются элементами(проекциями) вектора или координатами точки A, а количество элементов в векторе называется размерностью этого вектора. Положение элемента ai определяется индексом i, где i = 1,2,· ··,n. Элементы вектора записываются в виде столбца.
ВЕКТОРЫ И МАТРИЦЫ