Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМ
Содержание
- 1. КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМ
- 2. КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМВ основе
- 3. КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМФункция с секретом
- 4. RSA Алгоритм шифрования, в основе сложная задача
- 5. Задача. Зашифровать аббревиатуру RSA при p=17, q=31.
- 6. Слайд 6
- 7. ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬЧисло, зависящее от сообщения и
- 8. ЦИФРОВАЯ ПОДПИСЬ: ОТЛИЧИЯ ОТ СОБСТВЕННОРУЧНОЙСП. Не
- 9. ЦИФРОВАЯ ПОДПИСЬ: структура и требованияЭЦП включает
- 10. ЦИФРОВАЯ ПОДПИСЬ: ОБЩИЕ СХЕМЫ1. Схемы на
- 11. ЦИФРОВАЯ ПОДПИСЬ : ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.Основан на
- 12. ЦИФРОВАЯ ПОДПИСЬ : ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.Алгоритм подписи
- 13. ЦИФРОВАЯ ПОДПИСЬ : ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.Замечания.1. Число
- 14. ЦИФРОВАЯ ПОДПИСЬ: АЛГОРИТМЫ, ПОСТРОЕННЫЕ ПО ПРИНЦИПУ
- 15. ОДНОРАЗОВАЯ ЦИФРОВАЯ ПОДПИСЬ СХЕМА Диффи-ЛампортаНужно подписать
- 16. ОДНОРАЗОВАЯ ЦИФРОВАЯ ПОДПИСЬ СХЕМА Диффи-Лампорта
- 17. ИНФРАСТРУКТУРА ОТКРЫТЫХ КЛЮЧЕЙИОК необходима для исключения возможности
- 18. СЕРТИФИКАТЫ ЭЦПСертификат – набор данных, заверенный ЭЦП
- 19. ТРЕБОВАНИЯ К СЕРТИФИКАТАМ Удостоверяющий центр – это
- 20. РЕКОМЕДАЦИИ ПО ГЕНЕРИРОВАНИЮ КЛЮЧЕЙ1) Ключи может
- 21. ЮРИДИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ЭЦПЮридические аспекты использования
- 22. КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫОбъекты - удаленные абоненты, взаимодействующие по
- 23. КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ (примеры задач) Протокол
- 24. ТЕХНОЛОГИЯ ОТКРЫТОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙЗадача. Организовать такую процедуру
- 25. ОТКРЫТОЕ РАСПРЕДЕЛЕНИЕ КЛЮЧЕЙ. ПРОТОКОЛ ДИФФИ-ХЕЛЛМАНА Алгоритм Основан
- 26. ОТКРЫТОЕ РАСПРЕДЕЛЕНИЕ КЛЮЧЕЙ. ПРОТОКОЛ ДИФФИ-ХЕЛЛМАНАПосле обмена вычисляют
- 27. ИНТЕРАКТИВНОЕ ДОКАЗАТЕЛЬСТВО С НУЛЕВЫМ РАЗГЛАШЕНИЕМД -доказывающий,
- 28. ДОКАЗАТЕЛЬСТВО С НУЛЕВЫМ РАЗГЛАШЕНИЕМАВСDПЕЩЕРА АЛИ-БАБЫЦель: Доказывающий
- 29. Доказательство с нулевым разглашениемФормальное определение в терминах
- 30. Доказательство с нулевым разглашениемПолнота
- 31. Доказательство с нулевым разглашениемНулевое разглашение Для любой
- 32. ZK – доказательство «Изоморфизм графов»Рассмотрим графы G1
- 33. ZK – доказательство «Изоморфизм графов». Доказывающий выбирает
- 34. ZK – доказательство «Изоморфизм графов»Доказательство принимается, если
- 35. ПРОТОКОЛ АУТЕНТИФИКАЦИИ ФИАТА - ШАМИРАОтносится к
- 36. ПРОТОКОЛ АУТЕНТИФИКАЦИИ ФИАТА - ШАМИРА2.3. А
- 37. KERBEROSKerberos –это сервер аутентификации, (доверенная третья сторона)
- 38. KERBEROS. Kerberos не полагается на средства аутентификации,
- 39. KERBEROS28
- 40. ОТ ЧЕГО KERBEROS НЕ ЗАЩИЩАЕТАтаки на
- 41. ОТ ЧЕГО KERBEROS НЕ ЗАЩИЩАЕТПовторное использование
- 42. Слайд 42
- 43. Слайд 43
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
СЕРВИСЫ БЕЗОПАСНОСТИ.
ИДЕНТИФИКАЦИЯ И АУТЕНТИФИКАЦИЯ
Пестунова Тамара Михайловна
кандидат технических наук,
доцент
Слайд 2 КРИПТОГРАФИЯ
С ОТКРЫТЫМ КЛЮЧОМ
В основе теоретико-сложностный подход.
Гипотеза P≠
NP .
Односторонние функции F: X→ Y
а) существует полиномиальный алгоритм
вычисления y=F(x);б) не существует полиномиального алгоритма инвертирования функции F, т.е. решения уравнения F(x)=y относительно x .
Более сильное требование, чем принадлежность к NP-полным проблемам, т.к. требуется отсутствие полиномиального алгоритма почти всюду.
19
Слайд 3КРИПТОГРАФИЯ
С ОТКРЫТЫМ КЛЮЧОМ
Функция с секретом f K : X→
Y
а) при любом k существует полиномиальный алгоритм вычисления f K;
б)
при неизвестном k не существует полиномиального алгоритма инвертирования данной функции;в) при известном k существует полиномиальный алгоритм ее инвертирования.
Дифи У., Хеллман М. Защищенность и имитостойкость. Введение в криптографию // ТИИЭР т.67, №3, 1979
20
Слайд 4RSA
Алгоритм шифрования, в основе сложная задача факторизации больших чисел
1. Абонент выбирает пару простых чисел: p и q
вычисляет и публикует n=pq 2.Функция Эйлера: φ(n) = (p-1)(q-1)
3. Случайное e
4. Вычисляем d: ed=1 (mod φ(n))
5. Открытый ключ: (n,e)
6. Секретный ключ: (p, q, φ(n), d)
Шифрование: s=te (mod n)
Расшифрование: t=sd (mod n)
20
Слайд 5Задача. Зашифровать аббревиатуру RSA при p=17, q=31.
Решение. 1) Вычисляем
модуль n=p∙q=17∙31=527
2) Функция Эйлера φ(n)=(p-1)(q-1)=480.
3) Случайное е, т.ч. (е, φ(n))=1, например е = 7. 4) Вычисляем d, т.ч. e∙d=1(mod 480) , d=343, т.к.
343∙7=2401=480∙5+1
5) Переведем слово «RSA» в числовой вид:
R → 1810 = (10010)2
S → 1910 = (10011)2
A→ 110 = (00001)2
Общая последовательность (с учетом диапазона [0,526]):
RSA → (100101001100001) → (100101001),(100001) = (M1 = 297, M2 = 33)
RSA-пример
Слайд 6
6) Шифруем последовательно M1 и M2
С1 = Ek (M1) = M1e (mod 527) = 2977 (mod 527) = 474 С2 = Ek (M2) = M2e (mod 527) = 337 (mod 527) = 407
Получаем шифрограмму: С= (474,407)
7) Расшифрование
Dk (C1) = C1d (mod 527) = 474 343 (mod 527) = 297
Dk (C2) = C2d (mod 527) = 407 343 (mod 527) = 33
Для упрощения вычислений можно использовать соотношение:
343=256+64+16+4+2+1
Домашнее задание: написать программу на языке, реализующую RSA, проверить
Пример для теста – зашифровать и расшифровать последовательность, включающую свои имя и фамилию (без пробела) + 3 собственных примера.
RSA-пример
(продолжение)
Слайд 7ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ
Число, зависящее от сообщения и от некоторого секретного,
известного только подписывающему субъекту ключа.
Легко проверяема, проверку подписи может
осуществить каждый без получения доступа к секретному ключу. При возникновении спорной ситуации (отказ от подписи, подделка подписи), третья сторона должна иметь возможность разрешить спор.
Таким образом, решаются три задачи:
аутентификация источника сообщения,
установление целостности сообщения,
невозможность отказа от подписи конкретного сообщения.
32
Слайд 8ЦИФРОВАЯ ПОДПИСЬ:
ОТЛИЧИЯ ОТ СОБСТВЕННОРУЧНОЙ
СП. Не зависит от подписываемого текст,
всегда одинаковая
ЦП. Зависит от текста, почти всегда разная
СП. Неразрывна связана
с подписывающим лицом, ЦП. Определяется секретным ключом, может быть утеряна.
СП. Неотделима от носителя, каждый экземпляр подписывается отдельно.
ЦП. Верна для всех копий.
СП. Не требует доп. механизмов для реализации.
ЦП. Требует доп. механизмов ( алгоритмы, вычисления)
СП. Не требует поддерживающей инфраструктуры.
ЦП. Нужна доверенная инфраструктура сертификатов открытых ключей
33
Слайд 9ЦИФРОВАЯ ПОДПИСЬ:
структура и требования
ЭЦП включает два алгоритма:
Алгоритм вычисления
подписи и Алгоритм проверки подписи.
Основные требования:
Исключить возможность получения подписи
без знания секретного ключа Гарантировать возможность проверки подписи без знания секретного ключа.
Надежность подписи обеспечивается сложностью трех задач:
Подделки подписи (нахождение значения подписи лицам, не являющимся владельцем ЭЦП)
Создания подписанного сообщения (нахождение хотя бы одного сообщения с правильным значением подписи)
Подмены сообщения (подбор двух разных сообщений с одинаковым значением подписи)
34
Слайд 10ЦИФРОВАЯ ПОДПИСЬ:
ОБЩИЕ СХЕМЫ
1. Схемы на основе симметричных систем шифрования.
2.
Схемы на основе специально разработанных алгоритмов вычисления и проверки подписи.
3.
Схемы на основе шифрования с открытыми ключами (с восстановлением текста.)
(E,D) - пара преобразований, А - автор, П- получатель, М - сообщение,
S - подпись автора.
E зависит от открытого ключа, D - от секретного.
A: S=D(M) П: E(S)= M.
Требования: M= E (D(M)) для всех M;
невозможно вычислить D(M) без знания секретного ключа.
Возможно: данные подписываются, потом шифруются
35
Слайд 11ЦИФРОВАЯ ПОДПИСЬ :
ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.
Основан на вычислении логарифма в конечном
поле.
p - простое число,
Z(p) - конечное поле,
w - примитивный
элемент в Z(p).Выбрать случайное число 1≤a ≤ p -2
(a - секретный ключ).
Вычислить b= w a mod p .
((p, w, b)- открытый ключ).
36
Слайд 12ЦИФРОВАЯ ПОДПИСЬ :
ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.
Алгоритм подписи
1. Выбрать случайное число
1≤r ≤ p -2;
2. Вычислить c = w r mod
p ;3. Для x=M вычислить d = (x- a∙c)r -1 mod (p-1) ;
4. S=(c, d).
Алгоритм проверки. b с c d ≡ w x (mod p ).
36
Слайд 13ЦИФРОВАЯ ПОДПИСЬ :
ПРОТОКОЛ ЭЛЬ-ГАМАЛЯ.
Замечания.
1. Число r должно уничтожаться сразу
после вычисления подписи. Иначе секретный ключ вычисляется
a=(x- r∙d)c -1 mod
(p-1)2. Число r должно быть случайным, не должно повторяться для разных подписей . На шаге 3 реально обычно берется не x=M, а x=h(M) - свертка, полученная с помощью хэш-функции.
3. На одном секретном ключе можно выработать ЭЦП для многих сообщений
37
Слайд 14ЦИФРОВАЯ ПОДПИСЬ:
АЛГОРИТМЫ, ПОСТРОЕННЫЕ ПО ПРИНЦИПУ
ПРОТОКОЛА ЭЛЬ-ГАМАЛЯ
Схема проверки подписи
вида
α A β B≡ γ C (mod p ),
где (А,В,С) – перестановка элементов (±x, ±d, ±c )
заложена во многих стандартных алгоритмах ЭЦП, в том числе в
ГОСТ 34-10-94 и DSS.
38
Слайд 15ОДНОРАЗОВАЯ ЦИФРОВАЯ ПОДПИСЬ
СХЕМА Диффи-Лампорта
Нужно подписать сообщение M=(m1m2…mn), где
mi из {0,1}
Подписывающий
1) выбирает
2n случайн. секретных ключей: K=[(k10,k11), (k20,k21),…,
(kn0,kn1)] 2n случайных чисел из {0,1}:
S=[(s10,s11), (s20,s21), … , (sn0,sn1)]
2) вычисляет
Rij=Ekij(sij) , где j из {0,1}, i=1,2,…,n
3) Публикует наборы
S и R=[(R10,R11), (R20,R21), … , (Rn0,Rn1)]
Подпись для M имеет вид (k1m1, k2m2, … , knmn)
Проверка подписи: Rij=Ekij(sij), где j=mi, i=1,2,…,n
38
Слайд 16ОДНОРАЗОВАЯ ЦИФРОВАЯ ПОДПИСЬ
СХЕМА Диффи-Лампорта
(продолжение)
Недостатки:
1) Слишком большой размер
ключа
Можно хранить только секретный ключ k , и на
его основе формировать всю последовательность kij=Ek (i,j)
2) После проверки весь секретный ключ или его часть становится известны проверяющему,
поэтому система одноразовая
Слайд 17ИНФРАСТРУКТУРА ОТКРЫТЫХ КЛЮЧЕЙ
ИОК необходима для исключения возможности подделки открытого ключа
лицами, которые хотели бы выдать себя в качестве владельца секретного
ключа.ИОК включает в себя сеть центров сертификации открытых ключей.
Цель – обеспечить подтверждение достоверности принадлежности открытого ключа заявленному владельцу.
39
Слайд 18СЕРТИФИКАТЫ ЭЦП
Сертификат – набор данных, заверенный ЭЦП центра сертификации, включающий
открытый ключ и дополнительны атрибуты.
Типовая структура сертификатов ключей определена
спецификациями X509, имеющих статус международного добровольного стандарта. Порядковый номер сертификата.
Идентификационный алгоритм ЭЦП.
Имя центра сертификации (удостоверяющего центра).
Срок действия ЭЦП.
Имя владельца сертификата.
Открытые ключи владельца сертификата.
Идентификационный алгоритм, ассоциированный с открытыми ключами владельца.
ЭЦП центра сертификации.
40
Слайд 19ТРЕБОВАНИЯ К СЕРТИФИКАТАМ
Удостоверяющий центр – это компонент глобальной службы
каталогов, отвечающий за управление криптографическими ключами пользователей
Свойства сертификатов:
Любой
пользователь, знающий ОК удостоверяющего центра (УЦ), может узнать ОК других клиентов УЦ и проверить целостность сертификата. Никто, кроме УЦ, не может модифицировать информацию о пользователе, без нарушения целостности сертификата.
В Х509 не описываются конкретные процедуры генерации ключей, но дается ряд общих рекомендаций.
41
Слайд 20РЕКОМЕДАЦИИ
ПО ГЕНЕРИРОВАНИЮ КЛЮЧЕЙ
1) Ключи может генерировать сам пользователь. Тогда
Секретный ключ не попадает в руки третьих лиц, но надо
решить проблему безопасности связи с УЦ.2) Ключи может генерировать доверенное лицо, тогда стоит задача безопасной доставки секретного ключа владельцу, а также предоставление достоверных данных в УЦ.
3) Ключи могут генерироваться УЦ, тогда должна быть решена задача безопасной передачи секретного ключа владельцу.
42
Слайд 21ЮРИДИЧЕСКИЕ АСПЕКТЫ
ИСПОЛЬЗОВАНИЯ ЭЦП
Юридические аспекты использования ЭЦП обусловлены необходи-мостью разрешения
споров, связанных с отказом от автор-ства, подделкой, возмещением убытков в
спорных ситуациях.Кто несет ответственность если подписанная сделка не состоялась;
Кто несет ответственность, если система взломана и выявлен факт подделки секретного ключа;
Какова ответственность уполномоченного по сертификатам, если открытый ключ сфальсифицирован;
Какова ответственность владельца в случае утраты ОК;
Кто несет ответственность при повреждении и разглашении секретного ключа;
Каков порядок разрешения споров.
43
Слайд 22КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ
Объекты - удаленные абоненты, взаимодействующие по открытой сети, в
общем случае не доверяющие друг другу.
Цель - решение некоторой
задачи. Имеется противник, преследующий свои цели (противником может быть не только внешняя сторона, но один или несколько абонентов или сервер).
Протокол - некоторый распределенный алгоритм, определяющий последовательность действий каждой из сторон.
16
Слайд 23
КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ (примеры задач)
Протокол подписания контракта (исключить ситуацию, когда
один подписал контракт, а другой нет).
Протокол подбрасывания монеты (не
допустить, чтобы подбрасывающий мог изменить результат подбрасывания после получения информации о догадке угадывающего). Протокол идентификации абонента (Один абонент должен доказать другому, что он именно тот, за кого себя выдает).
Протокол электронной подписи (обеспечить аутентификацию, проверку целостности сообщения, невозможность отказа от факта подписи конкретного сообщения)
Протокол разделения секрета (содержание секрета разделяется таким образом, что каждый из пользователей обладает его частью, но без участия всех участников восстановить его невозможно)
17
Слайд 24ТЕХНОЛОГИЯ ОТКРЫТОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ
Задача.
Организовать такую процедуру взаимодействия удаленных абонентов
А и В, чтобы выполнить следующие условия:
а) вначале у А
и В нет общей секретной информации, но в конце процедуры такая общая секретная информация вырабатывается (общий ключ) ;
б) пассивный противник, который перехватывает все передачи информации и знает, что хотят получить А и В, не может восстановить общий ключ.
29
Слайд 25ОТКРЫТОЕ РАСПРЕДЕЛЕНИЕ КЛЮЧЕЙ. ПРОТОКОЛ ДИФФИ-ХЕЛЛМАНА
Алгоритм Основан на общепризнанной трудной
задаче дискретного логарифмирования,
т.е. инвертирования функции aX (mod p), где p
– простое число . Абоненты А и В выбирают натуральные числа xA и xB соответственно.
Вычисляют yA= aXA (mod p) и yB= aXB (mod p) .
Обмениваются результатами по сети. При этом p и a общедоступны.
30
Слайд 26ОТКРЫТОЕ РАСПРЕДЕЛЕНИЕ КЛЮЧЕЙ. ПРОТОКОЛ ДИФФИ-ХЕЛЛМАНА
После обмена вычисляют новые значения
A:
(yB ) XA = (aXB) XA (mod p),
B: (yA) XB
= (aXA )XB (mod p). У абонентов появился общий элемент aXА XВ.
Противник знает p, a, aXА, aXВ и хочет узнать aXА XВ
В настоящее время неизвестно более эффективных действий , чем дискретное логарифмирование - является труднорешаемой задачей.
31
Слайд 27ИНТЕРАКТИВНОЕ ДОКАЗАТЕЛЬСТВО
С НУЛЕВЫМ РАЗГЛАШЕНИЕМ
Д -доказывающий,
П- проверяющий,
У -
доказываемое утверждение
Д хочет доказать П, что У истинно. П без
помощи Д не может проверить истинность У. Число раундов не ограничено. Требования к протоколу:а) полнота (если У истинно, то Д убедит П признать это);
б) корректность (если У ложно, то Д вряд ли убедит П , что У истинно)
в) нулевое разглашение (в результате работы протокола П не увеличит свои знания об У, т.е. Не сможет извлечь никакой информации, почему У истинно).
18
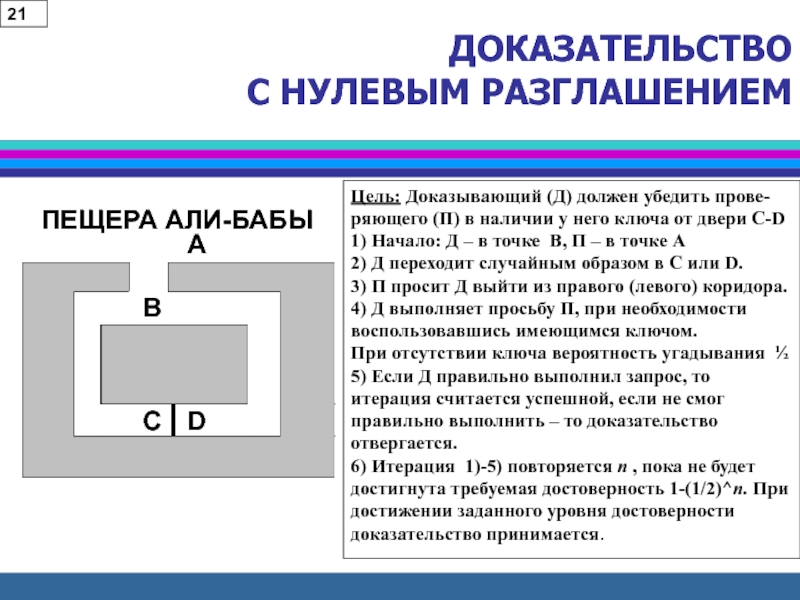
Слайд 28ДОКАЗАТЕЛЬСТВО
С НУЛЕВЫМ РАЗГЛАШЕНИЕМ
А
В
С
D
ПЕЩЕРА АЛИ-БАБЫ
Цель: Доказывающий (Д) должен убедить прове-ряющего
(П) в наличии у него ключа от двери C-D
1) Начало:
Д – в точке В, П – в точке А 2) Д переходит случайным образом в С или D.
3) П просит Д выйти из правого (левого) коридора.
4) Д выполняет просьбу П, при необходимости воспользовавшись имеющимся ключом.
При отсутствии ключа вероятность угадывания ½
5) Если Д правильно выполнил запрос, то итерация считается успешной, если не смог правильно выполнить – то доказательство отвергается.
6) Итерация 1)-5) повторяется n , пока не будет достигнута требуемая достоверность 1-(1/2)^n. При достижении заданного уровня достоверности доказательство принимается.
21
Слайд 29Доказательство с нулевым разглашением
Формальное определение в терминах машин Тьюринга (МТ)
Интерактивным доказательством для языка L
называется пара интерактивных МТ (P(x),
V(x)), где P – моделирует доказывающего,
V – моделирует проверяющего,
х – входное слово допустимого МТ языка L,
[P(x), V(x)] – слово на выходе
22
Слайд 30Доказательство с нулевым разглашением
Полнота ∀х Вер{[ P(x),
V(x)] =1}=1
Если оба участника следуют протоколу, то доказательство будет
принято Корректность ∀P* и полинома p
при x∉ L достаточно большой длины
Вер{[ P*(x), V(x)] =1} < 1 / p(|x|)
Если противник будет пытаться доказывать ложное утверждение, как угодно отклоняясь от протокола, то вероятность успеха для него пренебрежимо мала
22
Слайд 31Доказательство с нулевым разглашением
Нулевое разглашение
Для любой полиномиальной вероятностной МТ
V *,
существует вероятностная МТ MV*
работающая в среднем
за полиномиальное время, т.ч ∀х ∈ L MV* (x) = [ P(x), V*(x)] Защищает доказывающего от нечестного проверяющего:
Как бы ни отклонялся проверяющий от действий ,
предписанных протоколом (использует V * вместо V),
он сможет при этом получить только такую информацию,
которую и сам может самостоятельно вычислить
в среднем за полиномиальное время
22
Слайд 32ZK – доказательство «Изоморфизм графов»
Рассмотрим графы
G1 = (X,U1) и
G0 = (X,U0) ,
т.ч. G1 = ϕ (G0), где
ϕ – изоморфизм Изоморфизм - перестановка на множестве вершин X0, такая что
ребро (x,y) существует в графе G0 тогда и только тогда,
когда ребро (ϕ (x), ϕ(y)) существует в графе G1.
(обозначается G1 ≅ G0 )
23
Слайд 33ZK – доказательство «Изоморфизм графов»
. Доказывающий
выбирает случайную перестановку π
на множестве вершин X, вычисляет H = π (G1) и
посылает H проверяющему.. Проверяющий
выбирает случайный бит α и посылает его доказывающему.
. Если α = 1 , то
доказывающий отсылает проверяющему перестановку π ,
иначе – π ○ ϕ.
. Если полученная проверяющим перестановка не является изоморфизмом между Gα и H, то доказательство отвергается.
Иначе выполняется следующая итерация протокола.
23
Слайд 34ZK – доказательство «Изоморфизм графов»
Доказательство принимается,
если все проверки ш.
4 выполнены достаточное количество раз
(с учетом заданной вероятности достоверности)
и всегда давали положительный результат.
Данный протокол является протоколом с абсолютно нулевым разглашением для языка «изоморфизм графов»
23
Слайд 35ПРОТОКОЛ АУТЕНТИФИКАЦИИ
ФИАТА - ШАМИРА
Относится к числу протоколов «нулевого разглашения».
Основан на сложности задачи извлечения корня (аналогична факторизации)
1.Предварительный этап.
1.1. Доверенный центр T выбирает два простых числа p и q, рассылает всем доказывающим число n=pq.
1.2. А выбирает секрет s, т.ч. (s,n)=1, 1≤s≤n-1.
вычисляет v = s2 (mod n),
2. Итерация.
2.1. А выбирает случайное z, т.ч. 1
отправляет x проверяющему B
2.2. B выбирает случайный бит с и отправляет его А
24
Слайд 36ПРОТОКОЛ АУТЕНТИФИКАЦИИ
ФИАТА - ШАМИРА
2.3. А вычисляет y =z, если
с = 0
y =zs, если с = 1 и отправляет y проверяющему B
2.2. B принимает итерацию, если y2 = xvc (mod n).
Комментарий.
Полнота – непосредственно следует из вычисления формулы
Корректность. Например, пусть некто пытается выдать себя за А, подбирая значение x, не зная секрета: x= z2 / v.
Тогда он сможет дать правильный ответ при c=1,
но не сможет ответить правильно при с=0,
( надо вычислить корень из V, что является труднорешаемой задачей).
25
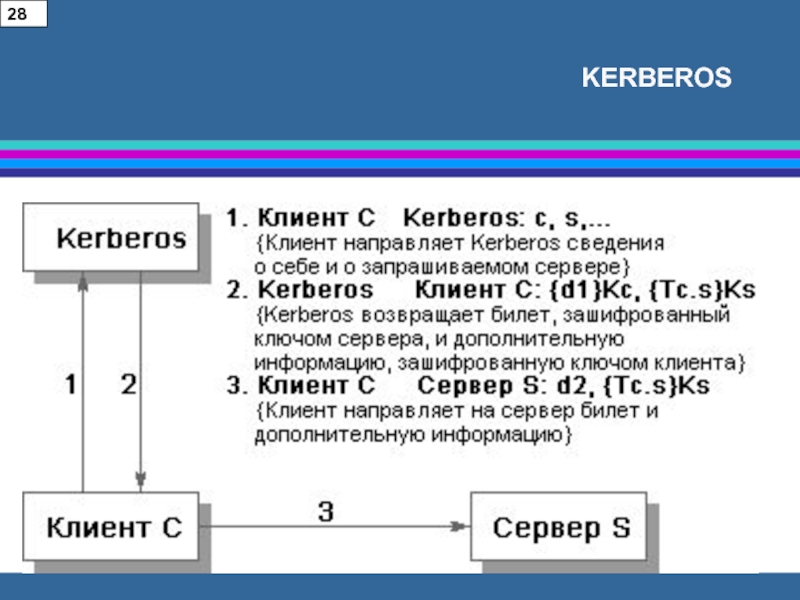
Слайд 37KERBEROS
Kerberos –это сервер аутентификации, (доверенная третья сторона) .
Функции: владеет
секретными ключами обслуживаемых субъектов и помогает им в попарной проверке
подлинности.Предоставляет средства проверки подлинности субъектов,
Условия абонентов: незащищенная сеть,
возможность перехвата,
модификации,
дополнения пересылаемой информации.
26
Слайд 38KERBEROS
.
Kerberos не полагается
на средства аутентификации, операционных систем сетевых
компьютеров,
на подлинность сетевых адресов,
на физическую защищенность сетевых компьютеров
(кроме тех, на которых работает сервер Kerberos). Физическая реализация Kerberos —
один или несколько серверов проверки подлинности,
функционирующих на физически защищенных компьютерах.
Серверы поддерживают базу данных субъектов и их секретных ключей.
26
Слайд 40ОТ ЧЕГО KERBEROS
НЕ ЗАЩИЩАЕТ
Атаки на доступность. отражение таких атак
и реакция на "нормальные" отказы возлагается на пользователей и администраторов.
Кража секретных ключей. Забота о сохранности своих ключей лежит на субъектах.
Угадывание паролей.
По слабому паролю можно вычислить секретный ключ и расшифровать полученную от Kerberos информацию.
При использовании "троянца" злоумышленник может узнать пароли многих пользователей.
След-но Kerberos все же предполагает некоторый базовый уровень защищенности обслуживаемых компьютеров.
27
Слайд 41ОТ ЧЕГО KERBEROS
НЕ ЗАЩИЩАЕТ
Повторное использование идентификаторов субъектов. Т
Теоретически возможно:
новый субъект Kerberos получит тот же идентификатор, что был у
ранее выбывшего субъекта.Возможно, что этот идентификатор остался в списках управления доступом какой-либо системы в сети.
Тогда новый субъект унаследует права доступа выбывшего.
Рассогласование часов на компьютерах.
Допустимая погрешность часов может устанавливаться индивидуально для каждого сервера.
Если синхронизация часов выполняется сетевыми средствами, соответствующий протокол должен сам заботиться о безопасности.
Более подробно о KERBEROS – см., например,
http://www.jetinfo.ru/1996/12-13/1/article1.12-13.1996.html
27




























![КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМ Доказательство с нулевым разглашениемПолнота ∀х Вер{[ P(x), V(x)] =1}=1 Если Доказательство с нулевым разглашениемПолнота ∀х Вер{[ P(x), V(x)] =1}=1 Если оба участника следуют протоколу,](/img/thumbs/3fbc96462407c9bfe0880ad7faf71f7e-800x.jpg)