Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геом Поиск Локализация
Содержание
- 1. Геом Поиск Локализация
- 2. 06.04.2007Геометрический поиск Локализация точки 2Геометрический поискПланарные
- 3. 06.04.2007Геометрический поиск Локализация точки 2Геометрический поискПланарные
- 4. 06.04.2007Геометрический поиск Локализация точки 2Формула Эйлера:
- 5. 06.04.2007Геометрический поиск Локализация точки 2Стереографическая проекцияvv′N
- 6. 06.04.2007Геометрический поиск Локализация точки 2Следствие 1:
- 7. 06.04.2007Геометрический поиск Локализация точки 2Следствие 2б:Для
- 8. 06.04.2007Геометрический поиск Локализация точки 2Плоские триангуляцииТриангуляция:
- 9. 06.04.2007Геометрический поиск Локализация точки 2Представление ППЛГ
- 10. 06.04.2007Геометрический поиск Локализация точки 2Представление ППЛГ Реберный список с двойными связями (РСДС) e1e6e7e4e5e2e3v4v3v1v5f4f3f2f1v2
- 11. 06.04.2007Геометрический поиск Локализация точки 2массивы входов:по
- 12. 06.04.2007Геометрический поиск Локализация точки 2Представление ППЛГ
- 13. 06.04.2007Геометрический поиск Локализация точки 2Представление ППЛГ
- 14. 06.04.2007Геометрический поиск Локализация точки 2Множество C
- 15. 06.04.2007Геометрический поиск Локализация точки 2Построение ПММЦ Балансировка весов ребер1111111112111111131221
- 16. 06.04.2007Геометрический поиск Локализация точки 2Регуляризация графа Метод заметания
- 17. 06.04.2007Геометрический поиск Локализация точки 2Метод детализации
- 18. 06.04.2007Геометрический поиск Локализация точки 2Локализация точкиМетод трапеций (Зайделя) будет позжеКонец лекции
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 106.04.2007
Геометрический поиск Локализация точки 2
Вычислительная геометрия
Лекция 6
Геометрический поиск
Локализация точки
Продолжение
Метод
трапеций (Зайделя) позже
Слайд 206.04.2007
Геометрический поиск Локализация точки 2
Геометрический поиск
Планарные графы. Планарное прямолинейное
подразбиение плоскости
Представление ППЛГ. Реберный список с двойными связями
Метод цепей (продолжение)
Метод
детализации триангуляцииСлайд 306.04.2007
Геометрический поиск Локализация точки 2
Геометрический поиск
Планарные графы
Планарное прямолинейное подразбиение
плоскости
Граф G = (V, E) называется планарным, если его можно
уложить на плоскости без самопересечений. Планарное подразбиение или карта порождается прямолинейной укладкой ребер планарного графа на плоскости.
V = { v1, v2, …, vn } – вершины,
E = { e1, e2, …, em } – ребра,
{ f1, f2, …, fl } – грани,
n – число вершин,
m – число ребер,
l – число граней
n = 5 m = 6
l = 3
5 + 3 = 6 + 2
f2
f1
f3
f2
f1
n = 6 m = 6
l = 2
6 + 2 = 6 + 2
f1
n = 5 m = 4
l = 1
5 + 1 = 4 + 2
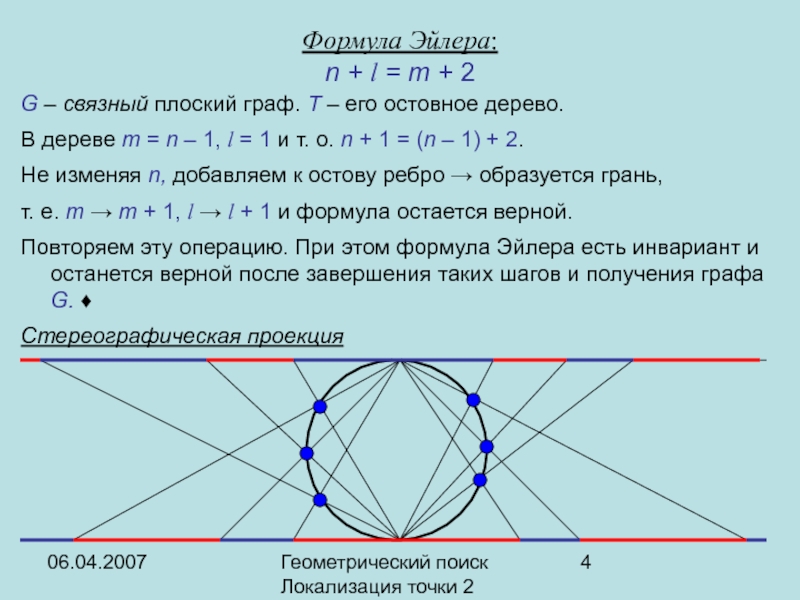
Формула Эйлера:
n + l = m + 2
Слайд 406.04.2007
Геометрический поиск Локализация точки 2
Формула Эйлера:
n + l =
m + 2
G – связный плоский граф. T – его
остовное дерево. В дереве m = n – 1, l = 1 и т. о. n + 1 = (n – 1) + 2.
Не изменяя n, добавляем к остову ребро → образуется грань,
т. е. m → m + 1, l → l + 1 и формула остается верной.
Повторяем эту операцию. При этом формула Эйлера есть инвариант и останется верной после завершения таких шагов и получения графа G. ♦
Стереографическая проекция
Слайд 606.04.2007
Геометрический поиск Локализация точки 2
Следствие 1:
Во всяком выпуклом
многограннике n + l = m + 2
Следствие 2а:
Для связного
планарного графа m ≤ 3n – 6 при n ≥ 3.Формула Эйлера:
n + l = m + 2
(т.к. граф без петель и параллельных ребер)
Т.о. 2m ≥ 3l .
l = m + 2 – n → 2m ≥ 3(m + 2 – n ) → m ≤ 3n – 6 ♦
d (fi) – степень грани (число ребер границы, мосты – дважды)
Слайд 706.04.2007
Геометрический поиск Локализация точки 2
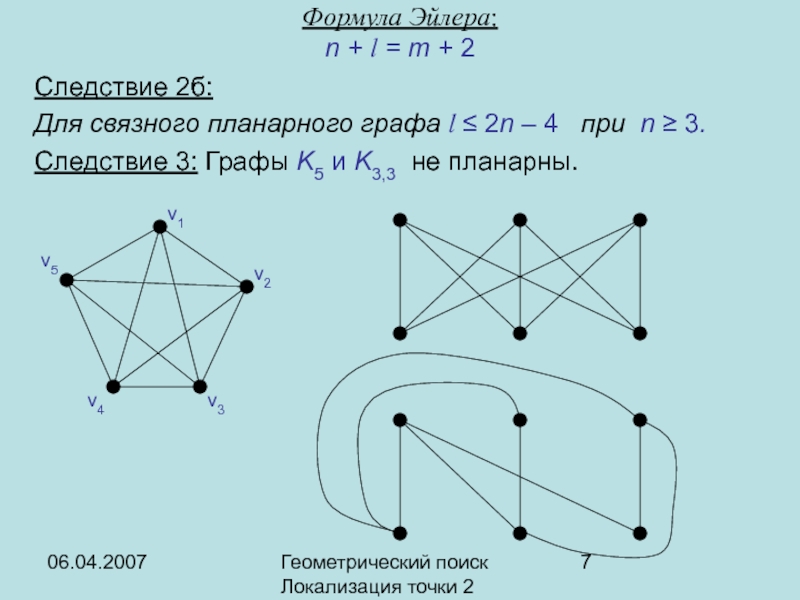
Следствие 2б:
Для связного планарного графа
l ≤ 2n – 4 при n ≥ 3.
Следствие
3: Графы K5 и K3,3 не планарны.Формула Эйлера:
n + l = m + 2
Слайд 806.04.2007
Геометрический поиск Локализация точки 2
Плоские триангуляции
Триангуляция: все конечные грани
– треугольники.
Триангуляция множества точек – триангуляция выпуклой оболочки.
Плоская триангуляция:
связный плоский граф, каждая грань которого (в том числе и внешняя) – треугольник.В этом случае m = 3n – 6 и l = 2n – 4
n = 3
m = 3
l = 2
n := n + 1
m := m + 3
l := l + 2
n := n + 1
m := m + 3
l := l + 2
n := n + 1
m := m + 2
l := l + 1
Слайд 906.04.2007
Геометрический поиск Локализация точки 2
Представление ППЛГ
Реберный список с двойными
связями (РСДС)
Основная компонента (элемент списка) РСДС – реберный узел
v6
f2
v5
v4
v3
v2
v1
f1
p2
p1
ek
Слайд 1006.04.2007
Геометрический поиск Локализация точки 2
Представление ППЛГ
Реберный список с двойными
связями (РСДС)
e1
e6
e7
e4
e5
e2
e3
v4
v3
v1
v5
f4
f3
f2
f1
v2
Слайд 1106.04.2007
Геометрический поиск Локализация точки 2
массивы входов:
по вершинам head_V [1..n]
по граням head_F [1..l]
Представление ППЛГ
Реберный список с
двойными связями (РСДС)
Слайд 1206.04.2007
Геометрический поиск Локализация точки 2
Представление ППЛГ
Реберный список с двойными
связями (РСДС)
Процедура «Инцидентные ребра»
(см. файл MS Word «РеберныйСписокДС»)
Слайд 1306.04.2007
Геометрический поиск Локализация точки 2
Представление ППЛГ
Реберный список с двойными
связями (РСДС)
Процедура «Граница грани» (см. файл MS Word «РеберныйСписокДС»)
Слайд 1406.04.2007
Геометрический поиск Локализация точки 2
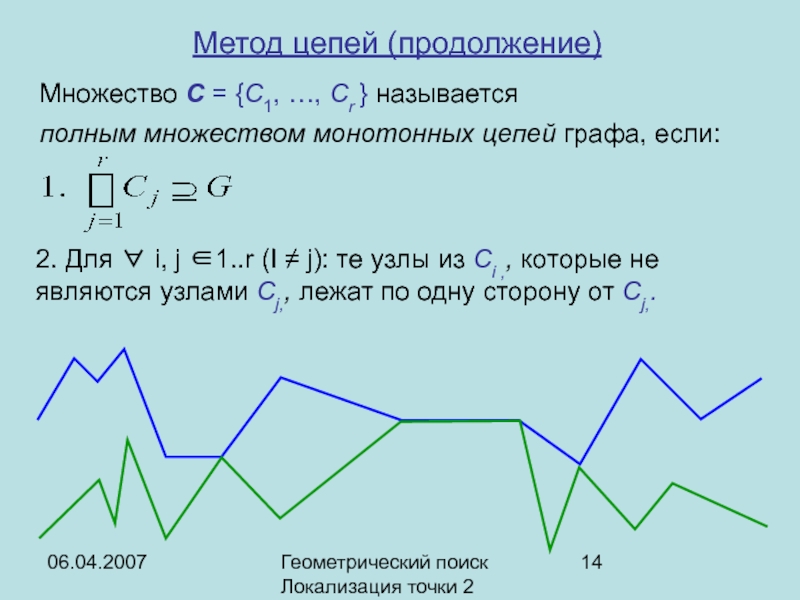
Множество C = {C1, …,
Cr } называется
полным множеством монотонных цепей графа, если:
Метод
цепей (продолжение)2. Для ∀ i, j ∈1..r (I ≠ j): те узлы из Ci ,, которые не являются узлами Cj,, лежат по одну сторону от Cj,.








![Геом Поиск Локализация 06.04.2007Геометрический поиск Локализация точки 2массивы входов:по вершинам head_V [1..n] по граням 06.04.2007Геометрический поиск Локализация точки 2массивы входов:по вершинам head_V [1..n] по граням head_F [1..l] Представление](/img/thumbs/e0c299347e245dbef324ae89208f9c5c-800x.jpg)