Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тройной интеграл Виды поверхностей второго порядка Замена переменных в тройном интеграле Тройной интеграл в цилиндрических коор
Содержание
- 1. Тройной интеграл Виды поверхностей второго порядка Замена переменных в тройном интеграле Тройной интеграл в цилиндрических коор
- 2. Виды поверхностей второго порядкаЦилиндрические поверхностиВсякое уравнение, не
- 3. Виды поверхностей второго порядкаУравнениепредставляет на плоскости XOY
- 4. Эти уравнения представляют собой цилиндрические поверхности у
- 5. Поверхности вращенияУравнение поверхности содержит переменные x и
- 6. Зададим x = 0, и получим уравнение линии на плоскости YOZ:Пример 4параболоид вращенияВиды поверхностей второго порядка6/17
- 7. Зададим x = 0, и получим уравнение
- 8. Зададим x = 0, и получим уравнение
- 9. Замена переменных в тройном интегралеЗаменим переменные :определитель
- 10. Тогда справедлива формула замены переменной в тройном
- 11. Цилиндрические координатыПоложение точки M(x; y; z) в
- 12. Цилиндрические координаты точки связаны с ее декартовыми
- 13. Формула замены переменных примет вид:Внутренний интеграл берется
- 14. К цилиндрическим координатам удобно переходить в том
- 15. Dz = 1Приведем уравнение конуса к цилиндрическим
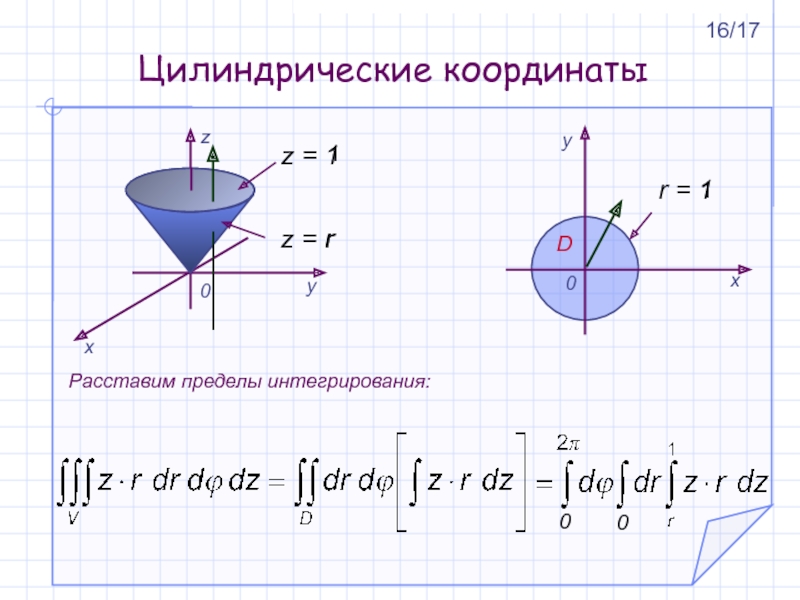
- 16. z = rРасставим пределы интегрирования:r1Цилиндрические координаты00116/17
- 17. Цилиндрические координаты17/17
- 18. Скачать презентанцию
Виды поверхностей второго порядкаЦилиндрические поверхностиВсякое уравнение, не содержащее переменной z и представляющее на плоскости XOY некоторую линию L представляет в пространстве цилиндрическую поверхность, у которой образующая параллельна оси OZ, а направляющей
Слайды и текст этой презентации
Слайд 1Тройной интеграл
Виды поверхностей второго порядка
Замена переменных в тройном интеграле
Тройной интеграл
в цилиндрических координатах
Слайд 2Виды поверхностей второго порядка
Цилиндрические поверхности
Всякое уравнение, не содержащее переменной z
и представляющее на плоскости XOY некоторую линию L представляет в
пространстве цилиндрическую поверхность, у которой образующая параллельна оси OZ, а направляющей служит линия L.1
Для построения этой поверхности рисуем линию на плоскости XOY с таким же уравнением, затем переносим ее параллельно оси OZ.
Правило
2/17
Слайд 3Виды поверхностей второго порядка
Уравнение
представляет на плоскости XOY эллипс с полуосями
а и b.
Пример 1
Пример 2
Уравнение
представляет на плоскости XOY гиперболу с
полуосями а и b.эллиптический цилиндр
гиперболический цилиндр
3/17
Слайд 4Эти уравнения представляют собой цилиндрические поверхности у которых образующие параллельны
осям OY и OX.
Уравнение
Пример 3
представляет на плоскости YOZ параболу.
параболический
цилиндрДля построения первой поверхности рисуем линию на плоскости XOZ, затем переносим ее параллельно оси OY , для построения второй поверхности рисуем линию на плоскости YOZ, затем переносим ее параллельно оси OX .
Виды поверхностей второго порядка
4/17
Слайд 5Поверхности вращения
Уравнение поверхности содержит переменные x и y в виде
2
Для
построения этой поверхности задаем x = 0, рисуем линию на
плоскости YOZ с уравнением , затем вращаем ее вокруг оси OZ.Правило
Аналогично изображаются поверхности:
(задаем x = 0, рисуем линию на плоскости YOZ , затем вращаем ее вокруг оси OY )
(задаем y = 0, рисуем линию на плоскости XOZ , затем вращаем ее вокруг оси OX )
Виды поверхностей второго порядка
5/17
Слайд 6Зададим x = 0, и получим уравнение линии на плоскости
YOZ:
Пример 4
параболоид вращения
Виды поверхностей второго порядка
6/17
Слайд 7
Зададим x = 0, и получим уравнение линии на плоскости
YOZ:
Пример 5
конус
- уравнения двух прямых
Виды поверхностей второго порядка
7/17
Слайд 8Зададим x = 0, и получим уравнение линии на плоскости
YOZ:
Пример 6
сфера
- уравнение окружности
В общем случае уравнение сферы с центром
в точке (a; b; c) и радиусом R:Виды поверхностей второго порядка
8/17
Слайд 9Замена переменных в тройном интеграле
Заменим переменные :
определитель Якоби (якобиан)
Пусть
в замкнутой области V пространства задана непрерывная функция F =
f(x, y, z).Пусть функции x, y и z имеют в некоторой области V* плоскости 0uvw непрерывные частные производные и не равный нулю определитель:
9/17
Слайд 10Тогда справедлива формула замены переменной в тройном интеграле:
Для вычисления тройного
интеграла наиболее часто используют так называемые цилиндрические и сферические координаты.
Замена
переменных в тройном интеграле10/17
Слайд 11Цилиндрические координаты
Положение точки M(x; y; z) в пространстве можно определить
заданием трех чисел r; φ; z.
r – длина радиус –
вектора проекции точки M на плоскость X0Y.r
φ – угол, образованный этим радиус – вектором с осью 0X.
φ
z – аппликата точки М.
z
M(x; y; z)
M(r; φ; z)
Эти три числа (r; φ; z) называются цилиндрическими координатами точки М.
11/17
Слайд 12Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
Возьмем
в качестве u, v, w цилиндрические координаты r, φ, z
и вычислим Якобиан преобразования:Цилиндрические координаты
12/17
Слайд 13Формула замены переменных примет вид:
Внутренний интеграл берется по переменной z,
пределы расставляются также, как в декартовых координатах (уравнения поверхностей должны
быть приведены к цилиндрическим координатам) .Оставшийся двойной интеграл – это интеграл в полярных координатах по области D.
Цилиндрические координаты
13/17
Слайд 14
К цилиндрическим координатам удобно переходить в том случае, если область
D (проекция области V на XOY) – круг или часть
круга или если область V образована цилиндрической поверхностью.Замечание
Вычислить
V – область, ограниченная верхней частью конуса
и плоскостью z = 1.
Цилиндрические координаты
14/17
Слайд 15
D
z = 1
Приведем уравнение конуса к цилиндрическим координатам:
z = r
Найдем
уравнение линии, ограничивающей область D:
В полярных координатах:
r = 1
r =
1Цилиндрические координаты
15/17
