Схемотехника электронных средств

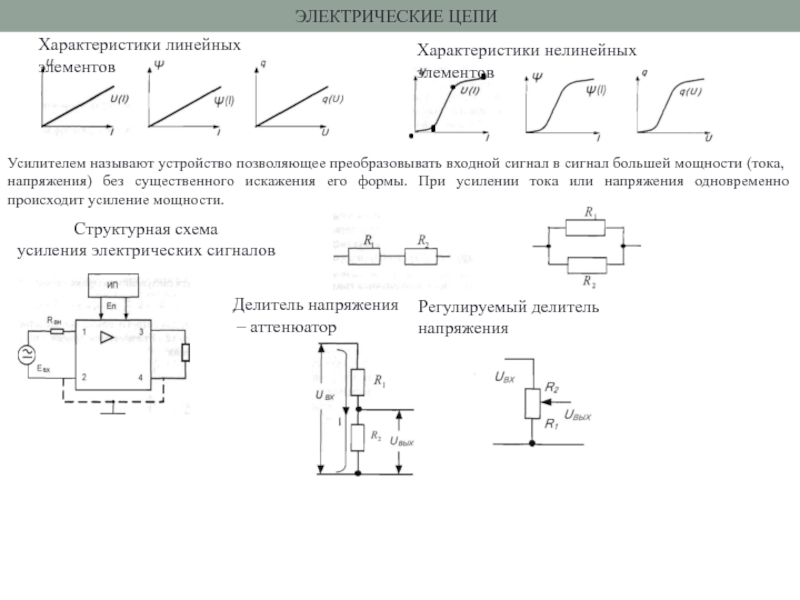
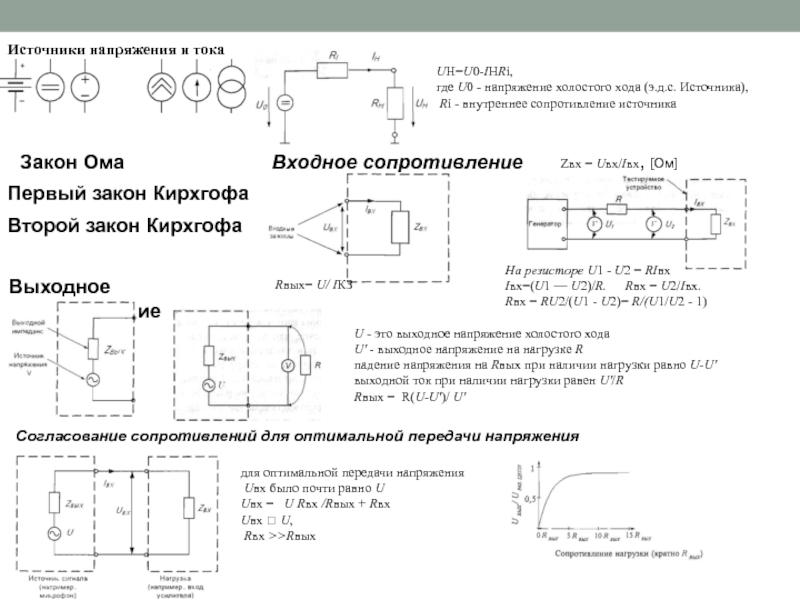
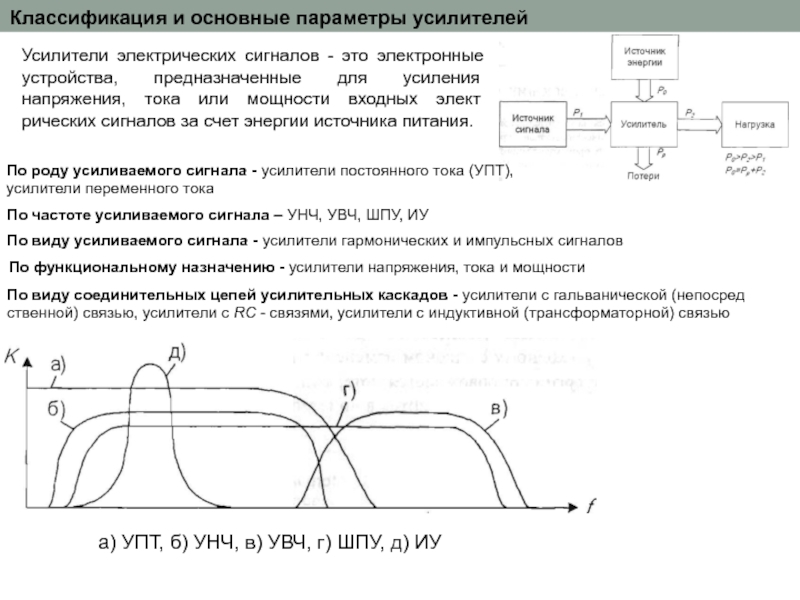
время, передаточная функция - комплексную переменную s, а амплитудно-фазовая частотная

характеристика - угловую частоту ω.
Прохождение сигналов через линейную цепь. Рассмотрим линейную цепь, на которую воздействует сигнал s(t). На выходе возникает реакция - выходной сигнал y(t) (рис.).
Известно, что при воздействии на линейную цепь гармонического сигнала s(t)=Smcos(ωt+ϕs), на выходе цепи устанавливается сигнал, форма которого тоже гармоническая: y(t) = Ymcos(ωt+ϕY). Гармонический сигнал - единственный сигнал, не изменяющий свою форму при прохождении через линейную электрическую цепь.

Пусть на линейную цепь воздействует сложный негармонический сигнал s(t). Форма сложного сигнала при прохождении через цепь будет искажаться. Для расчетов искажений выходного сигнала y(t) наиболее часто используются спектральные методы и их обобщения. Суть спектрального метода проста. Сложный сигнал с помощью рассмотренных выше спектральных разложений представляется в виде суммы гармонических колебаний. Затем находятся частичные реакции линейной цепи на каждый их гармонических входных сигна­лов. После этого, в соответствии с принципом суперпозиции результирующий выходной сигнал находится как сумма частичных реакций линейной цепи.
Спектральный метод анализа линейных цепей определяет два простых правила, которыми следует пользоваться при определении характера прохож­дения сигнала через эти цепи.
Во-первых, в зависимости от требований к форме выходного сигнала следует сравнить спектр входного сигнала и амплитудно-частотную характе­ристику цепи. Допустим, что требования к форме выходного сигнала доста­точно высоки, тогда форма АЧХ должна быть такой, чтобы без затухания пере­давать все значимые гармоники входного сигнала.
Во-вторых, в результате сравнения спектра сигнала и АЧХ линейной цепи можно оценить форму выходного сигнала.
В качестве примера рассмотрим прохождение прямоугольных импуль­сов через фильтр нижних частот. Прямоугольный импульс формируется набо­ром нечетных гармоник, однако за формирование фронта и среза отвечают высокие гармоники, а за формирование вершины импульса - нижние гармо­ники. При прохождении сигнала через фильтр высокие гармоники подавляют­ся, следовательно, в выходном сигнале уменьшится их амплитуда. Это приве­дет к тому, что фронты прямоугольных импульсов будут более пологими, а вершины не изменятся.

вход­ной сигнал в сигнал большей мощности (тока, напряжения) без существенного

искажения его формы. При усилении тока или напряжения одновременно происходит усиление мощности.

Структурная схема усиления электрических сигналов

Делитель напряжения
– аттенюатор

Регулируемый делитель напряжения

(э.д.с. Источника),
Ri - внутреннее сопротивление источника
Закон Ома
Первый закон Кирхгофа
Второй

закон Кирхгофа

Входное сопротивление

Zвx = Uвx/Iвx, [Ом]

На резисторе U1 - U2 = RIвx
Iвx=(U1 — U2)/R. Rвx = U2/Iвx.
Rвx = RU2/(U1 - U2)= R/(U1/U2 - 1)

Выходное сопротивление

Rвыx= U/ IКЗ

U - это выходное напряжение холостого хода
U' - выходное напряжение на нагрузке R
падение напряжения на Rвыx при наличии нагрузки равно U-U'
выходной ток при наличии нагрузки равен U'/R
Rвыx = R(U-U')/ U'

Согласование сопротивлений для оптимальной передачи напряжения

для оптимальной передачи напряжения
Uвx было почти равно U
Uвx = U Rвx /Rвыx + Rвx
Uвx  U,
Rвx >>Rвых

= Rвыx Xвx = -Xвыx
Согласование сопротивлений для оптимальной передачи тока
Максимум

входного тока Iвx , когда полное сопротивление в цепи выбирается возможно меньшим
При фиксированном Rвыx следует стремиться к возможно меньшему значению Rвx

устройства, пред­назначенные для усиления напряжения, тока или мощности входных элект­рических

сигналов за счет энергии источника питания.

По роду усиливаемого сигнала - усилители посто­янного тока (УПТ), усилители переменного тока

По частоте усиливаемого сигнала – УНЧ, УВЧ, ШПУ, ИУ

По виду усиливаемого сигнала - усилители гармоничес­ких и импульсных сигналов

По функциональному назначению - усилители напряже­ния, тока и мощности

По виду соединительных цепей усилительных каскадов - усилители с гальванической (непосред­ственной) связью, усилители с RC - связями, усилители с индуктивной (трансформаторной) связью

а) УПТ, б) УНЧ, в) УВЧ, г) ШПУ, д) ИУ

усилителя.
В зависимости от типа усиливаемой величины различают коэффициенты усиления по

напряжению КU, току КI или мощности КP.: КU =Uвых /Uвх , КI = Iвых /Iвх, КP =Pвых /Pвх,
КU (дБ) = 20lg КU; КI (дБ) = 20lgКI; КP(дБ) = 10lg КP
Для многокаскадного усилителя К = К1К2..КN К (дБ)= К1(дБ)+К2(дБ)+..+КN(дБ)

 

Амплитудная характеристика - это зависимость амплитуды выходно­го напряжения (тока) от амплитуды входного напряжения (тока).
Точка 1 соответствует сигналу шумов, измеряемому при нулевом входном сигнале
Точка 2 - минимальному входному напряжению, при котором мож­но различить сигнал на фоне шумов.
Участок 2-3 - это рабочий участок, на котором сохраняется пропорциональность между входным и выходным на­пряжениями усилителя.
После точки 3 наблюдается ограничение сигнала из-за попадания транзисторов в режим насыщения

Динамический диапазон усиления характеризует диапазон изменения входного сигнала D = Uвхмакс /Uвхмин.

выходного сигнала (тока, напряжения) от времени при скачкообразном входном воздействии.

Эта характеристика используется для определения динамических свойств устройства. Численно по данной характеристике определяют два параметра: время нарастания выходного напряжения tнар и перерегулирование выходного напряжения (выброс фронта импульса) δ.

Частотная, фазовая и переходная характеристики усилителя однозначно связаны друг с другом. Области верхних частот соответствует переходная харак­теристика в области малых времен, области низких частот - переходная характе­ристика в области больших времен.

Коэффициент полезного действия (КПД):
η= Pвых/P0 где Р0 - мощность, потребляемая усилителем от источника питания.
КПД характеризует экономичность усилителя. Особенно важен для мощных выходных каскадов.
Входное и выходное сопротивление . Их значения учитываются при согласовании усилителя с источником входного сигнала (датчиком) и с нагрузкой. В общем виде зна­чения входного и выходного сопротивлений носят комплексный характер и яв­ляются функцией частоты. Последняя зависимость особенно важна в случае дей­ствия на входе усилительного устройства непериодического сигнала.
Выходная мощность усилителя - эта та часть мощности, которая мо­жет быть выделена в нагрузке длительное время.

нелинейной зави­симостью выходного сигнала от входного, обусловленной нелинейностью ста­тических ВАХ

применяемых элементов,
2. с зависимостью коэф­фициента передачи усилителя от частоты.
Поэтому при анализе работы усили­телей рассматривают два вида искажений выходного сигнала по отношению к входному: нелинейные и линейные (частотные и фазовые), в результате кото­рых меняется как форма, так и частотный спектр усиливаемого сигнала.

Причина возникновения нелинейных искажений:
При воздействии на вход усилителя синусои­ды выходной сигнал кроме входной гармоники будет содержать ряд допол­нительных гармоник. Появление этих гармоник обусловлено зависимостью коэффициента усиления от величины входного сигнала. Следовательно, по­явление нелинейных искажений всегда связано с появлением на выходе до­полнительных, отсутствующих на входе гармонических составляющих.

 

Коэффициент гармоник (коэффициент нелинейных искажений) КГ для количественной оценки величины нелинейных искажений. Отношение величины высших гармоник к основной в вы­ходном сигнале, на вход усилителя подается синусоида:

сигнала из выходной цепи во входную.
Электрические цепи, обеспечивающие пере­дачу сигнала

из выходной цепи во входную , называются цепями обратной связи.
Выходной сигнал усилителя (в виде напряжения Uвых) через цепь обратной связи частично или полностью подается к схеме сложения. В ней происходит вычитание сигнала ОС UОС из входного сигнала Uвх. В ре­зультате этого на вход усилителя поступает сигнал, равный разности вход­ного сигнала и сигнала обратной связи UΣ.

Петлей обратной связи называют замкнутый контур, включающий в себя цепь ОС и часть усилителя между точками ее подключения. В качестве це­пей ОС часто используют пассивные цепи, коэффициенты преобразования и час­тотные свойства которых существенно влияют на свойства усилителей.
Местной обратной связью называют ОС, охватывающую отдель­ные каскады или части усилителя, а общей обратной связью - такую ОС, которая охватывает весь усилитель.
Обратную связь называют отрицательной, если ее сигнал вычитается из входного сигнала, и положительной, если сигнал ОС суммируется со вход­ным. При отрицательной ОС (OOС) коэффициент усиления усилителя умень­шается, а при положительной (ПОС) - увеличивается.

Из-за схемных особенностей усилителя и цепи ОС возможны вариан­ты, когда ОС существует только для медленно изменяющейся составляющей выходного сигнала, либо только для переменной составляющей его, либо для всего выходного сигнала. В таких случаях говорят, ОС реализована по по­стоянному, по переменному, а также по постоянному и переменному токам.

В зависимости от способа получения сигнала различают ОС по напря­жению (рис. а), когда снимаемый сигнал ОС пропорционален напряже­нию выходной цепи; ОС по току (рис. б), когда снимаемый сигнал про­порционален току выходной цепи.

последователь­ную схему введения ОС (рис. а), когда напряжение сигнала ОС

сумми­руется со входным напряжением; параллельную схему введения ОС (рис. б), когда ток цепи ОС суммируется с током входного сигнала.
Для количественной оценки степени влияния обратной связи использу­ют коэффициент обратной связи β, показывающий, какая часть выходного сигнала поступает на вход усилителя:
βU=Uoc/UBbIX, βI =IОС/IBbIX,
а также коэффициент петлевого усиления Кβ и (1 - Кβ) - глубину обратной связи.

обратной связи равен К, а благодаря обратной связи из входного

напряжения вычитается часть выходного (βUBbIX). На вход усилителя поступает напряжение, равное UBX - βUBbIX. Выходное напряжение больше входного в К раз:
UBbIX = К(UBX - βUBbIX )

и коэффициент усиления по напряжению при замкнутой цепи ООС равен КООС = К/(1+βК).
Обратная связь оказывает влияние практически на все основные характе­ристики усилителя. Введение ООС повышает стабильность основных характеристик усилителя. Если δК = ΔК/К - относительная нестабильность коэффи­циента усиления усилителя, где ΔК - абсолютная нестабильность, то относи­тельная нестабильность коэффициента усиления усилителя, охваченного ООС,
δКос = ΔКОС / КОС = δК/(1+βК).
Следовательно, в результате воздействия ООС нестабильность коэффи­циента усиления уменьшается в /(1+βК) раз.
При βК >> 1 коэффициент усиления усилителя, охваченного глубокой ООС, равен КООС ≈ 1/β.
-> Коэффициент усиле­ния усилителя с отрицательной обратной связью определяется только обрат­ной связью и не зависит от параметров самого усилителя.

Коэффициент усиления. Рассмотрим усилитель, обладающий конечным коэффициентом усиления и охваченный петлей ООС, образующий неинвертирующий усилитель

Применение ООС обеспечивает повышение стабильности коэффици­ента усиления при изменении параметров элементов, при смене активных элементов, изменении напряжения питания и т.д., снижение нелинейности, которая определяется изменениями коэффициента усиления в зависимости от уровня сигнала и собственных помех, возникающих в той части усилите­ля, которая охвачена ООС.
Отрицательная обратная связь позволяет уменьшить все воздействия на усилитель, охваченный ООС, но не компенсирует воздействий на цепь обратной связи. Поэтому в качестве элементов цепи ООС рекомендуется ис­пользовать резистивные делители, выполненные на высокостабильных ре­зисторах.
ООС оказывает влияние на входное и выходное сопротивление усилителя.
Последовательная ООС увеличивает входное сопротивление, что явля­ется положительным фактором:
ZBXОС=ZBX(1+βК), где ZBXОС, ZBX — входное сопротивление усилителя соответственно с ООС и без ООС.

ZBX в (1 + βК) раз.
В качестве примера последовательной ООС

схема неинвертирующего усилителя на ОУ. Входное сопротивление этой схемы определяется по формуле ZBXОС=ZBX(1+βК). Параллельная ООС в схеме инвертирующего усилителя на ОУ (рис.). Вход­ное сопротивление при введении ООС уменьшилось в (1 + βК ) и равно R1. Введение ООС по напряжению уменьшает выходное сопротивление усилителя ZBЫXОС =ZBЫX/(1 + βК), а ООС по току увеличивает ZBЫX на то же значение. Схемы инвертирующего и неинвертирующего усилителя содержат ООС по напряжению.

Влияние ООС на частотную характеристику усилителей.
Никакой усилитель не дает один и тот же коэффициент усиления на всех частотах. Коэффициент усиления любого усилителя начинает падать на высоких часто­тах, главным образом из-за его внутренней паразитной емкости. Это вы­зывает частотные искажения. ООС может скорректировать частотную характеристику в пределах интервала частот, на котором коэффициент усиле­ния без ОС остается много большим, чем усиление с обратной связью, в этих пределах применимо равенство КООС = 1/β и усиление не зависит от частоты.
На рис. приведены частотные характеристики усилителя на основе К140УД7. Верхняя кривая относится к разомкнутой петле обратной связи. Быстрое умень­шение усиления на высоких частотах введено умышленно с помощью вну­треннего конденсатора из соображений устойчивости. Кривая, расположенная ниже, показывает, как ООС выравнивает частотную характеристику за счет усиления: приведена характеристика усилителя с обратной связью и она доста­точно ровная вплоть до области частот, где коэффициент усиления с ООС достигает кривой, относящейся к случаю разомкнутой петли ОС.

? ООС расширяет полосу пропус­кания усилителя. Так как АЧХ усилителя однозначно определяет ФЧХ, то ООС оказывает благотворное влияние на нее, а соответственно уменьшают­ся частотные и фазовые искажения в схеме.
?влияние ООС позволяет улучшить характеристики уси­лителя: повысить стабильность коэффициента усиления; увеличить входное и уменьшить выходное сопротивление (последовательная ООС по напряже­нию), уменьшить входное и увеличить выходное сопротивление (параллель­ная 00С по току); расширить полосу пропускания усилителя; уменьшить нелинейные, частотные и фазовые искажения в схеме; уменьшить уровень собственных помех.
Уменьшение коэффициента усиления может быть скомпен­сировано введением дополнительных усилительных каскадов.