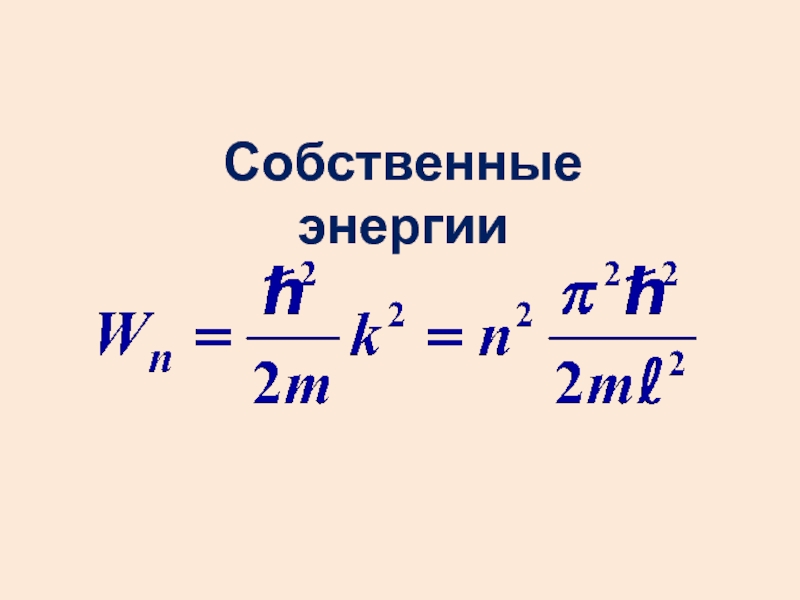Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение Шредингера
Содержание
- 1. Уравнение Шредингера
- 2. В 1926 г. швейцарский теоретик Эрвин Шредингер
- 3. Для частицы, движущейся в силовом поле:
- 4. оператор Лапласапотенциальная энергия частицы в силовом поле
- 5. Если пси-функция не зависит от времени, то
- 6. Волновая функция должна быть конечной, однозначной, непрерывной, интегрируемой и подчиняться условию нормировки
- 7. Уравнение Шредингера имеет решение только при некоторых
- 8. Чтобы решить уравнение Шредингера, надо задать потенциальную
- 9. Уравнение Шредингера – это уравнение движения микрочастицы.
- 10. Принцип причинности в квантовой механике состоит в
- 11. Движение свободной частицыПусть частица движется вдоль оси х. Для свободной частицы U=0. Тогдаили
- 12. Получили обычную связь энергии и импульса нерелятивистской частицы:
- 13. Решение уравнения имеет вид:константы интегрированияили
- 14. С учетом зависимости пси-функции от времениДля свободной
- 15. Волновое число, а, значит, и энергия частицы
- 16. Частица в одномерной потенциальной яме с бесконечно высокими стенками
- 17. Потенциальная энергия частицы:
- 18. Снаружи и на краях ямы частица быть
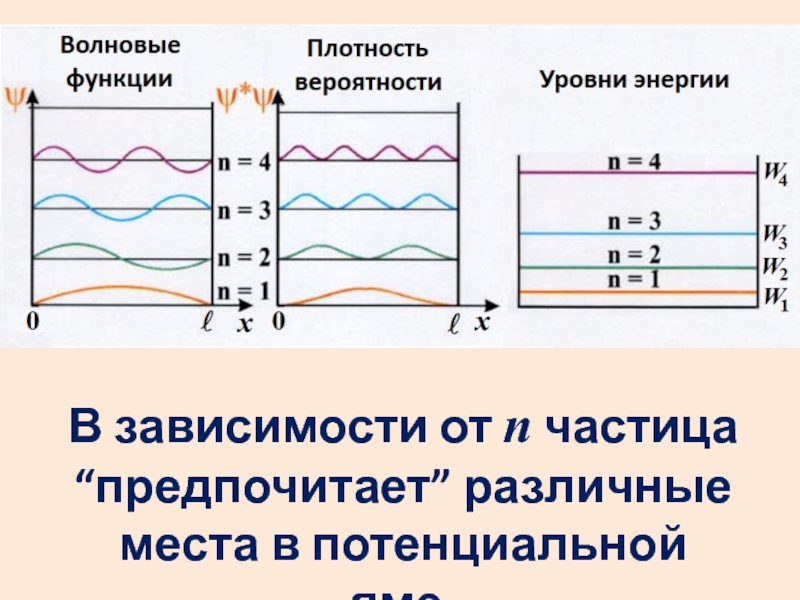
- 19. Собственные функциипредставляют собой стоячие волны де Бройля с узлами на краях ямы.
- 20. Собственные энергии
- 21. Энергия принимает дискретные значения – квантуется.Wn – уровни энергии,n – главное квантовое число.
- 22. В зависимости от n частица “предпочитает” различные места в потенциальной яме.
- 23. Расстояние между энергетическими уровнями:Относительное расстояние:
- 24. При больших квантовых числах Принцип соответствия Бора:
- 25. Линейный гармонический осцилляторГармоническим осциллятором называют частицу массой m, совершающую движение под действием квазиупругой силы
- 26. Потенциальная энергия такой частицы уравнение Шредингера
- 27. Так как частица движется в ограниченной области пространства, энергетический спектр будет дискретным. Собственные энергии:
- 28. Уровни отделены друг от друга на одну и ту же энергиюТакой спектр называют эквидистантным.
- 29. Состояние с наименьшей энергией называют основным.Энергия квантового осциллятора не может обращаться в нуль.
- 30. Движение частицы в основном состоянии называют нулевыми
- 31. При переходе между состояниями выделяется или затрачивается энергияв полном соответствии с гипотезой Планка.
- 32. Туннельный эффектТуннельный эффект - это «просачивание» микрочастицы
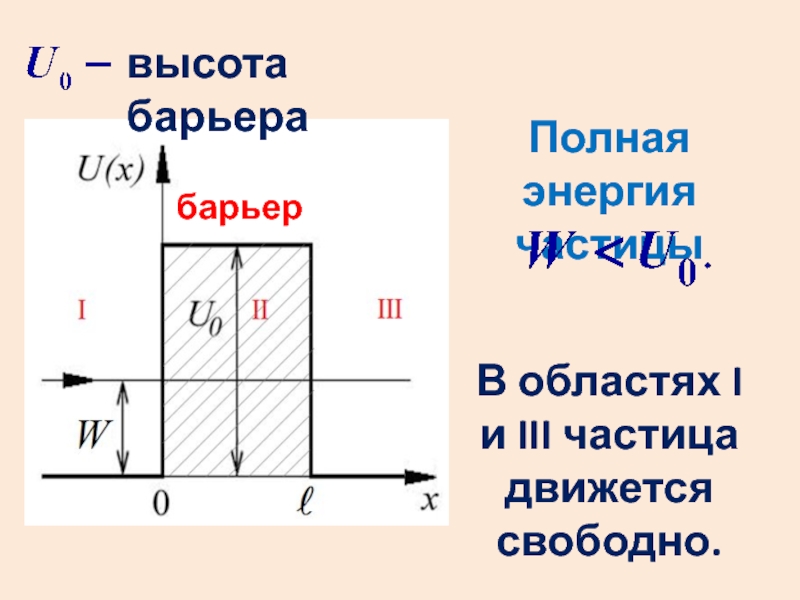
- 33. высота барьераПолная энергия частицыбарьерВ областях I и III частица движется свободно.
- 34. В областях I и III волновые функции
- 35. Слайд 35
- 36. Отношение интенсивностей прошедшей и падающей волн дает вероятность прохождения барьера частицей.Еще эту величину называют прозрачностью барьера.
- 37. Туннельный эффект широко используется в электронной микроскопии и микроэлектронике.
- 38. Радиоактивный альфа-распад – пример туннелирования частиц α-распад
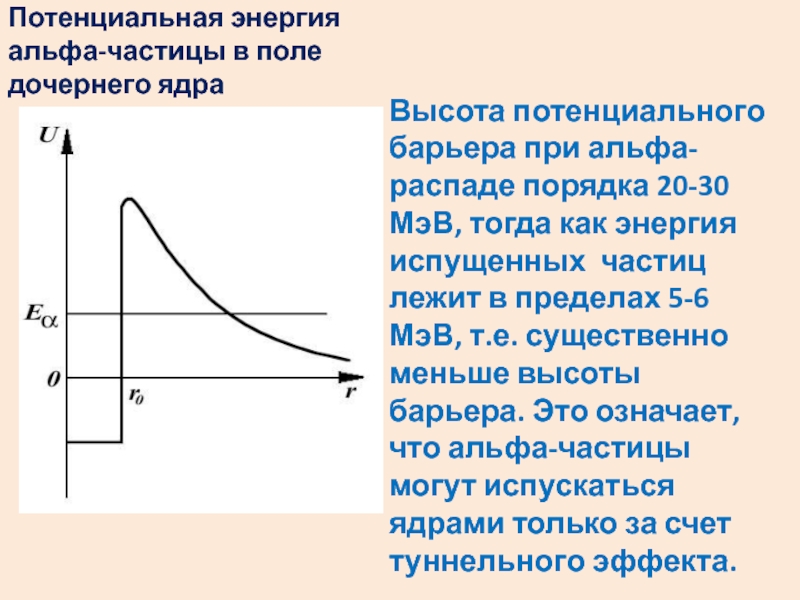
- 39. Потенциальная энергия альфа-частицы в поле дочернего ядра
- 40. Сканирующий туннельный микроскоп (СТМ) был создан в
- 41. Атомный силовой микроскоп. Принцип работы сканирующего зондового микроскопа
- 42. Остриё шипа
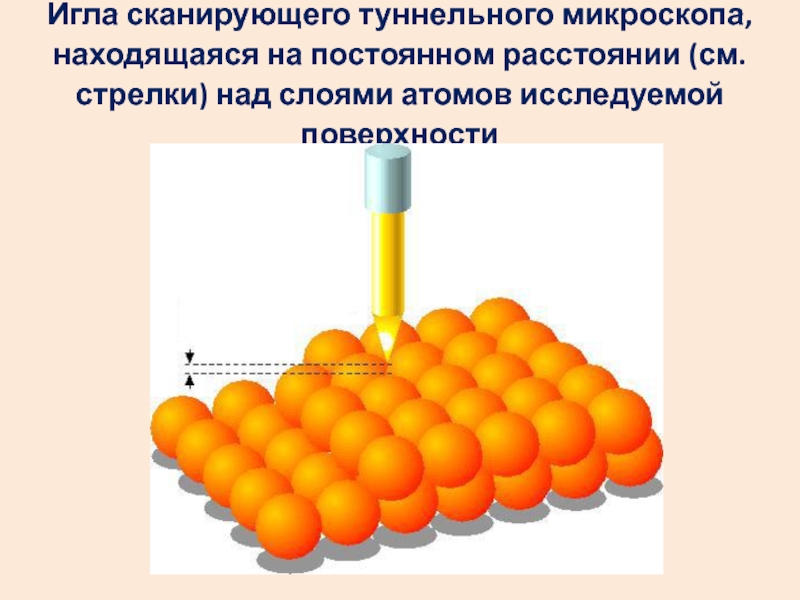
- 43. Игла сканирующего туннельного микроскопа, находящаяся на постоянном расстоянии (см. стрелки) над слоями атомов исследуемой поверхности
- 44. Изображение атомов углерода на поверхности графита, полученное
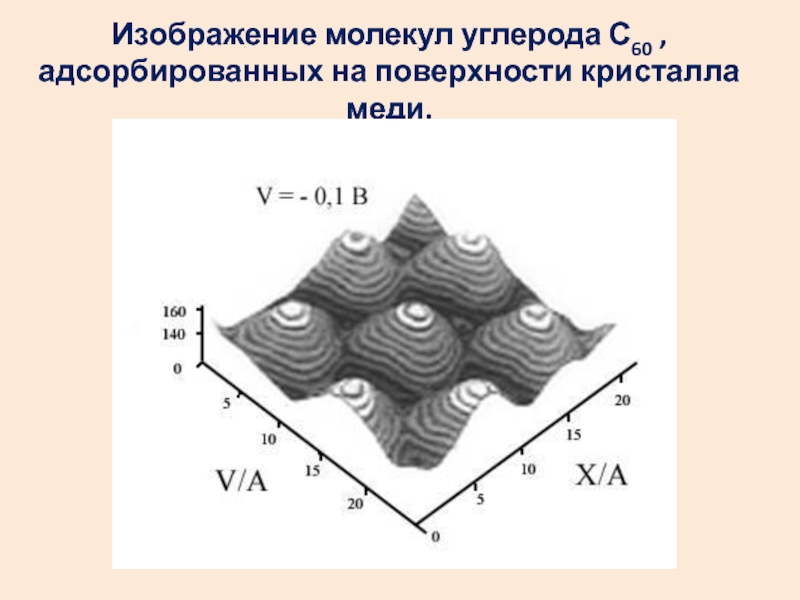
- 45. Изображение молекул углерода С60 , адсорбированных на поверхности кристалла меди.
- 46. Нанотехнология – это исследование и изготовление приборных структур нанометрового размера.
- 47. Атомная структура поверхности высокоориентированного пиролитического графита. Размер изображения 17х17х2 Å
- 48. Туннельная микроскопия с низкотемпературным сканированиемНадпись IBM составлена
- 49. «Квантовый коралл» - 48 атомов железа, расположенных в форме овала.
- 50. Скачать презентанцию
В 1926 г. швейцарский теоретик Эрвин Шредингер открыл фундаментальное уравнение, которому волны де Бройля удовлетворяют во всех случаях.
Слайды и текст этой презентации
Слайд 2В 1926 г. швейцарский теоретик Эрвин Шредингер открыл фундаментальное уравнение,
которому волны де Бройля удовлетворяют во всех случаях.
Слайд 5Если пси-функция не зависит от времени, то состояние частицы называют
стационарным.
Для этого состояния:
волновая функция стационарного состояния
полная энергия частицы
Слайд 6Волновая функция должна быть конечной, однозначной, непрерывной, интегрируемой и подчиняться
условию нормировки
Слайд 7Уравнение Шредингера имеет решение только при некоторых значениях энергии W.
Эти значения называют собственными значениями энергии.
Соответствующие волновые функции называют
собственными функциями.
Слайд 8Чтобы решить уравнение Шредингера, надо задать потенциальную энергию как функцию
координат и граничные условия для волновой функции. Решение представляет из
себя набор собственных значений энергии и собственных функций.
Слайд 9Уравнение Шредингера – это уравнение движения микрочастицы. Его роль та
же, что и второго закона Ньютона в классической механике.
Слайд 10Принцип причинности в квантовой механике состоит в том, что зная
волновую функцию в начальный момент времени, можно, применив уравнение Шредингера,
найти ее в последующие моменты времени.
Слайд 11Движение свободной частицы
Пусть частица движется вдоль оси х. Для свободной
частицы U=0. Тогда
или
Слайд 14С учетом зависимости пси-функции от времени
Для свободной частицы собственные функции
уравнения Шредингера – это плоские монохроматические волны де Бройля произвольных
частот.
Слайд 15
Волновое число, а, значит, и энергия частицы могут принимать любое
значение.
Энергетический спектр свободной частицы является сплошным.
Слайд 18Снаружи и на краях ямы частица быть не может: ψ
=0.
Внутри ямы:
Граничные условия: ψ(0) =0, ψ(l) =0.
Тогда В=0, т.к.
cos0≠0, а
Слайд 21Энергия принимает дискретные значения – квантуется.
Wn – уровни энергии,
n –
главное квантовое число.
Слайд 24При больших квантовых числах
Принцип соответствия Бора:
в пределе при
больших n законы квантовой механики переходят в законы классической физики.
Энергетический спектр становится непрерывным.
Слайд 25Линейный гармонический осциллятор
Гармоническим осциллятором называют частицу массой m, совершающую движение
под действием квазиупругой силы
Слайд 27Так как частица движется в ограниченной области пространства, энергетический спектр
будет дискретным.
Собственные энергии:
Слайд 29Состояние с наименьшей энергией
называют основным.
Энергия квантового осциллятора не может
обращаться в нуль.
Слайд 30Движение частицы в основном состоянии называют
нулевыми колебаниями.
Отличие от
нуля минимальной энергии квантового гармонического осциллятора — это следствие соотношения
неопределенностей Гейзенберга.
Слайд 31При переходе между состояниями выделяется или затрачивается энергия
в полном соответствии
с гипотезой Планка.
Слайд 32Туннельный эффект
Туннельный эффект - это «просачивание» микрочастицы сквозь потенциальный барьер,
т. е. проникновение в недоступную с классической точки зрения область
пространства.
Слайд 34В областях I и III волновые функции – плоские волны
де Бройля с амплитудами А1 и А3.
В области барьера
волновая функция убывает с расстоянием.
Слайд 36
Отношение интенсивностей прошедшей и падающей волн дает вероятность прохождения барьера
частицей.
Еще эту величину называют прозрачностью барьера.
Слайд 38Радиоактивный альфа-распад – пример туннелирования частиц
α-распад – это самопроизвольное
испускание радиоактивным ядром альфа-частицы, т.е. ядра атома гелия, состоящего из
двух протонов и двух нейтронов.
Слайд 39Потенциальная энергия альфа-частицы в поле дочернего ядра
Высота потенциального барьера
при альфа-распаде порядка 20-30 МэВ, тогда как энергия испущенных частиц
лежит в пределах 5-6 МэВ, т.е. существенно меньше высоты барьера. Это означает, что альфа-частицы могут испускаться ядрами только за счет туннельного эффекта.
Слайд 40Сканирующий туннельный микроскоп (СТМ) был создан в 1982 г сотрудниками
исследовательского отдела фирмы IBM Г. Биннигом и Х. Рёрером.
Туннельная
микроскопияК поверхности проводящего образца на расстояние, составляющее доли нанометра, подводится очень тонкое металлическое острие (игла). При приложении между образцом и иглой разности потенциалов в цепи появляется ток, обусловленный туннелированием электронов через зазор.
Слайд 43Игла сканирующего туннельного микроскопа, находящаяся на постоянном расстоянии (см. стрелки)
над слоями атомов исследуемой поверхности
Слайд 44Изображение атомов углерода на поверхности графита, полученное с помощью туннельного
микроскопа. Оранжевые линии - изображение электронных орбит, черные области - положение
ядер атомов графита.
Слайд 47Атомная структура поверхности высокоориентированного пиролитического графита. Размер изображения 17х17х2 Å
Слайд 48Туннельная микроскопия с низкотемпературным сканированием
Надпись IBM составлена из атомов ксенона.
Микроскоп,
способен визуализировать отдельные атомы на металлической или полупроводниковой поверхности.
