молекул
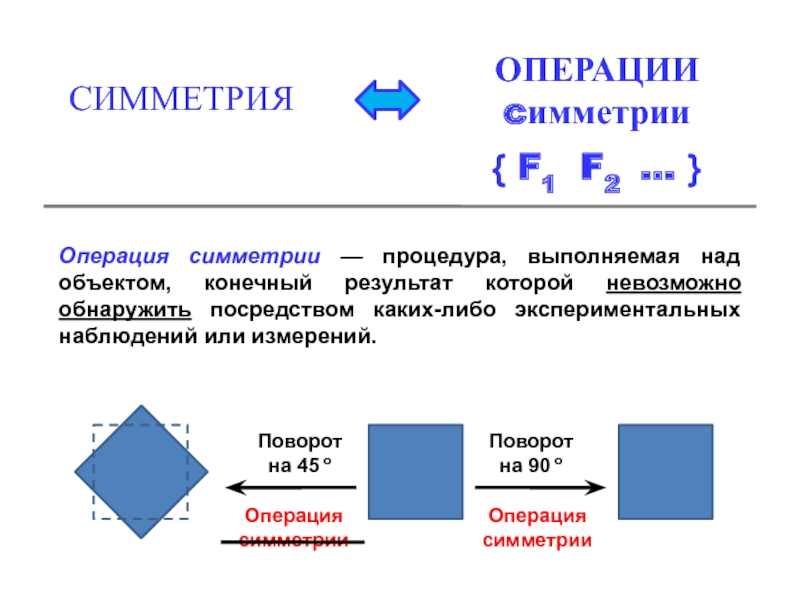
Правила отбора в спектроскопии
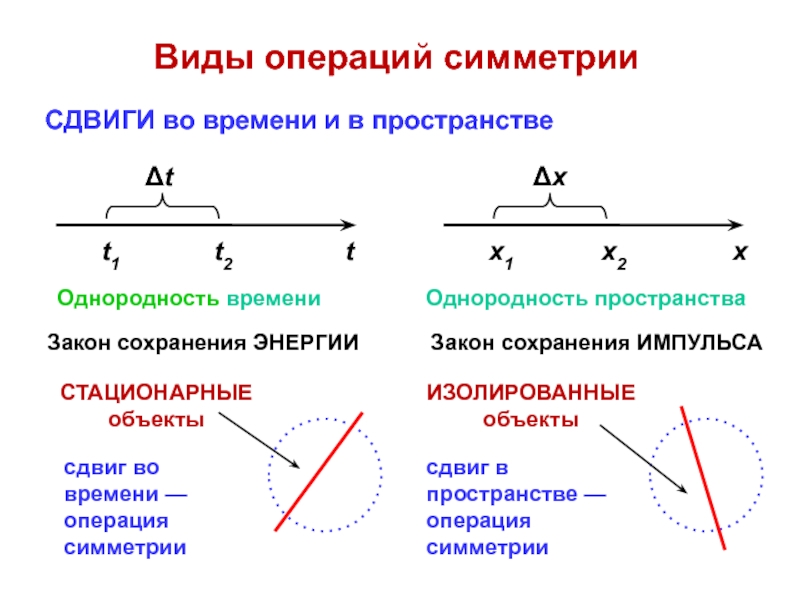
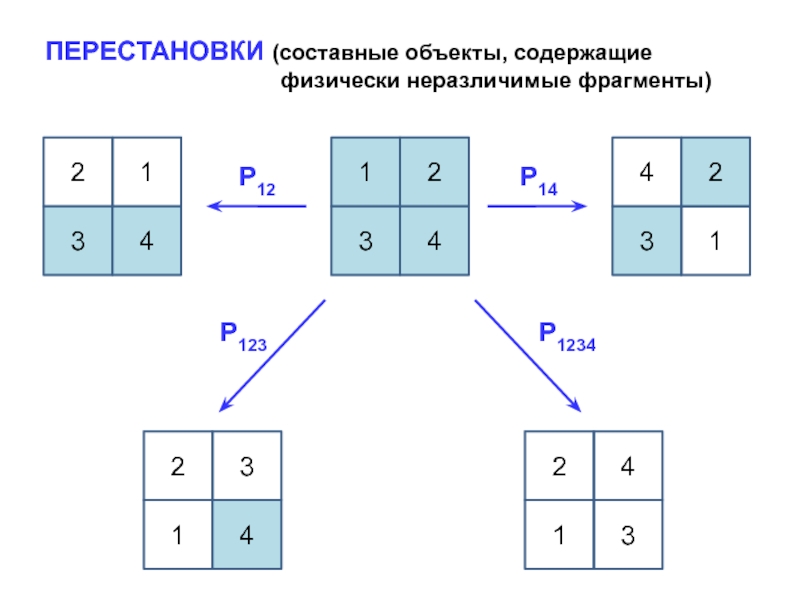
Разделение элементарных химических реакций на «разрешенные» и
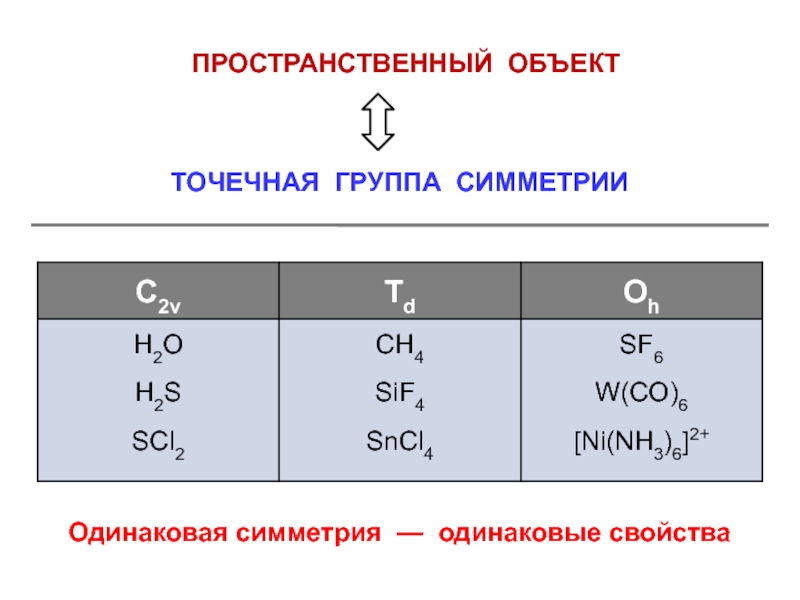
«запрещенные»Классификация свойств атомов и молекул по «типам симметрии»




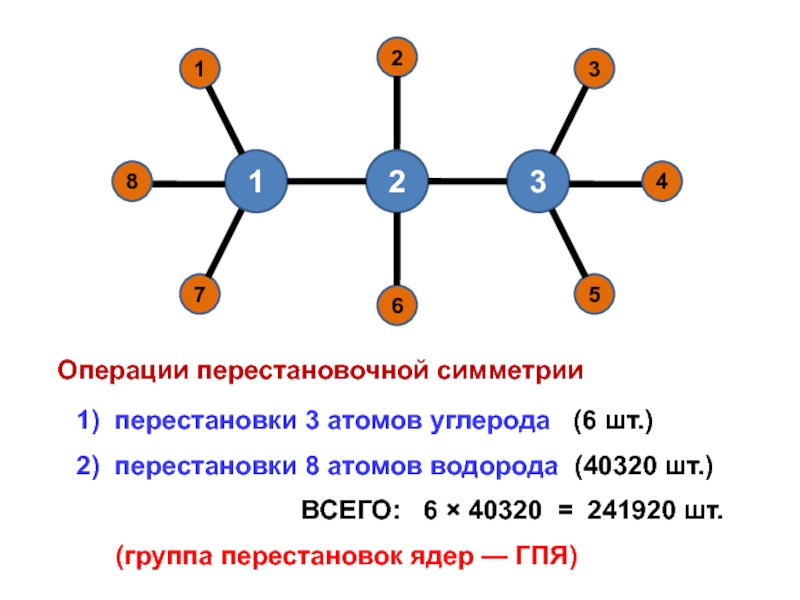
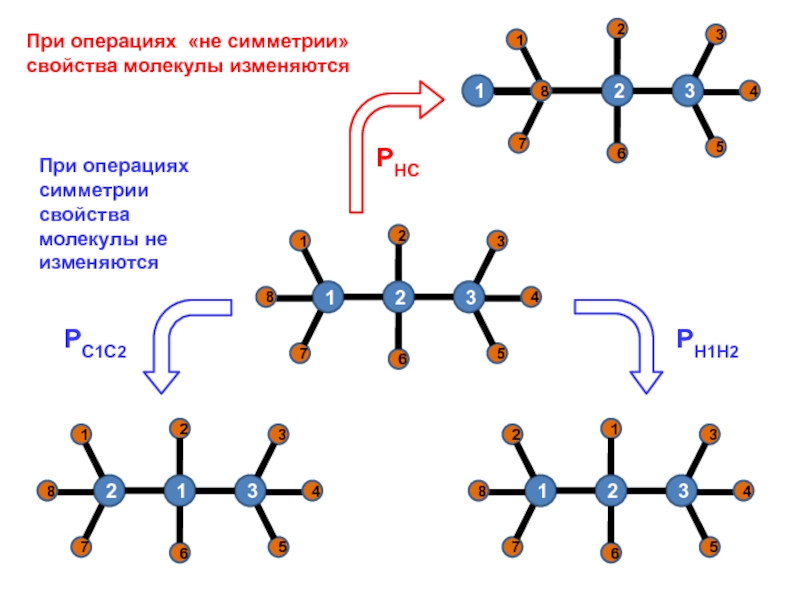
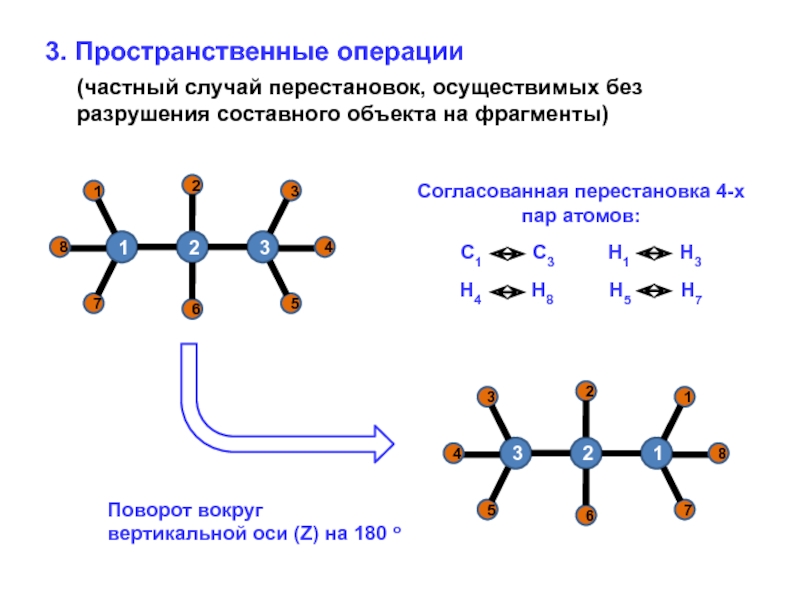

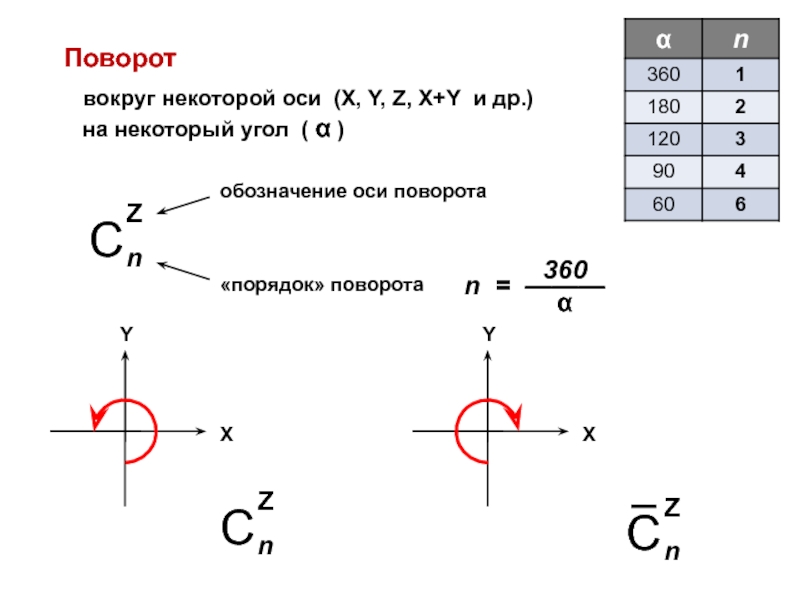
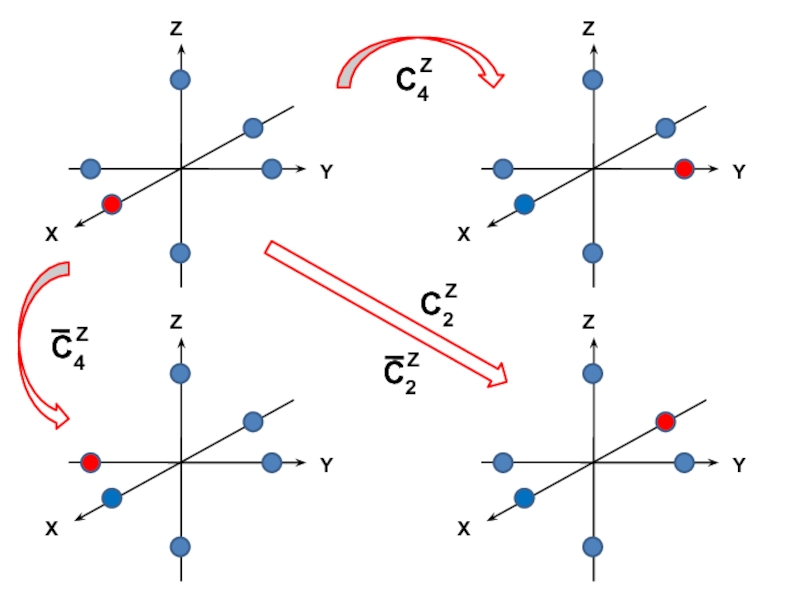


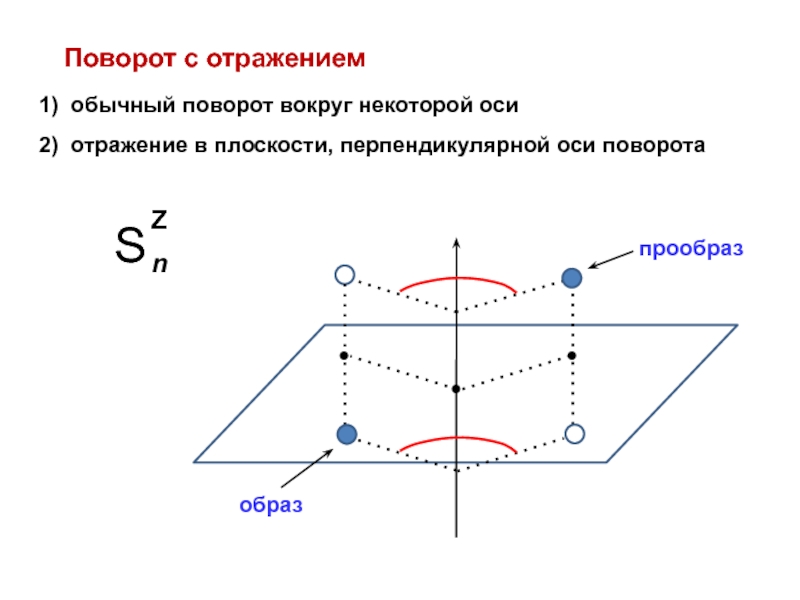
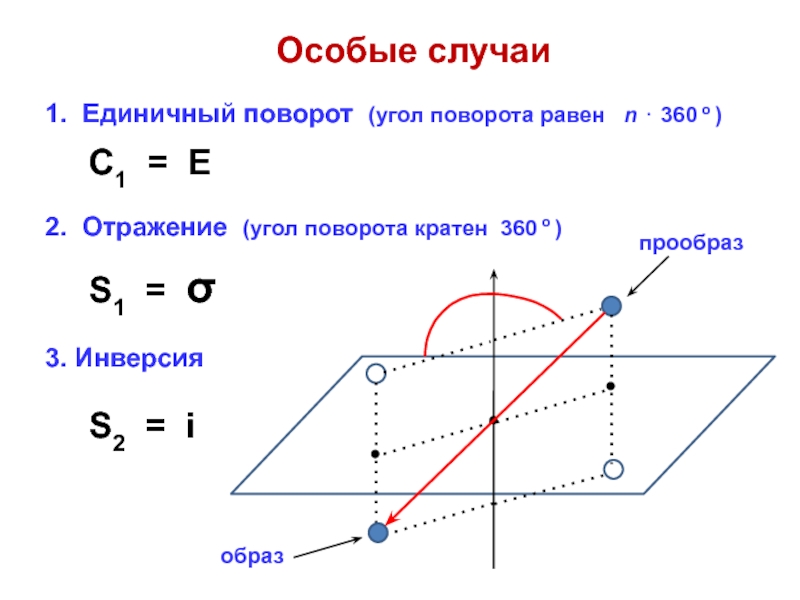
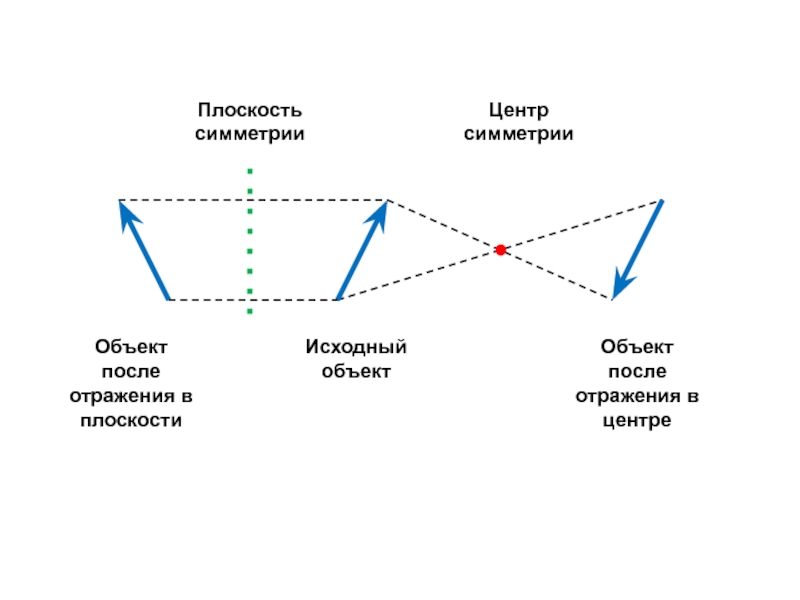
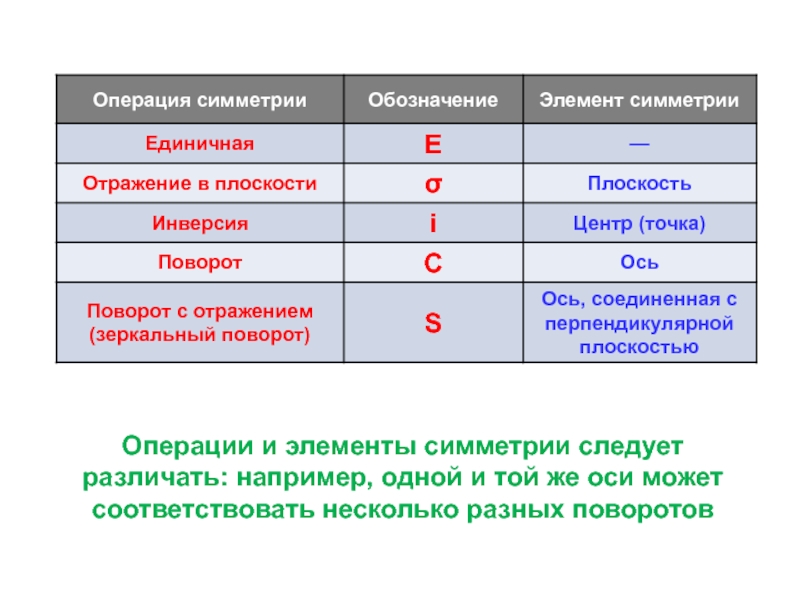

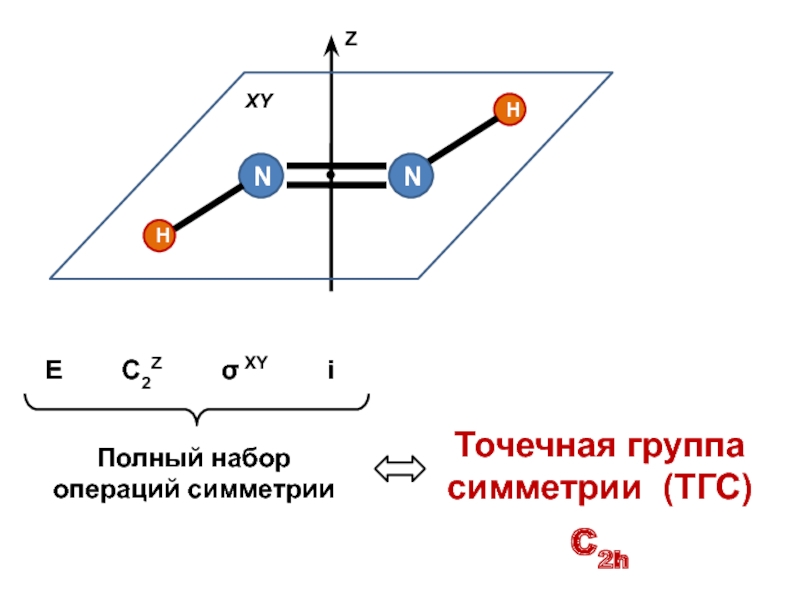
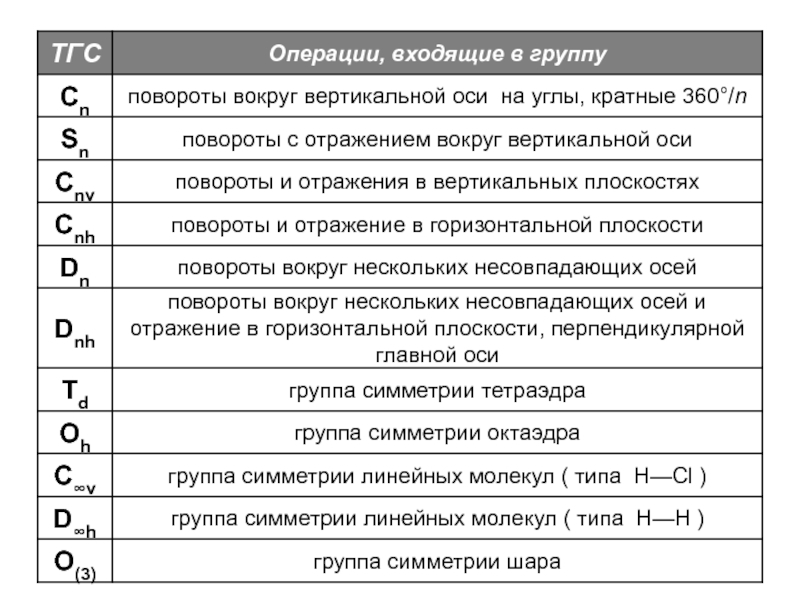






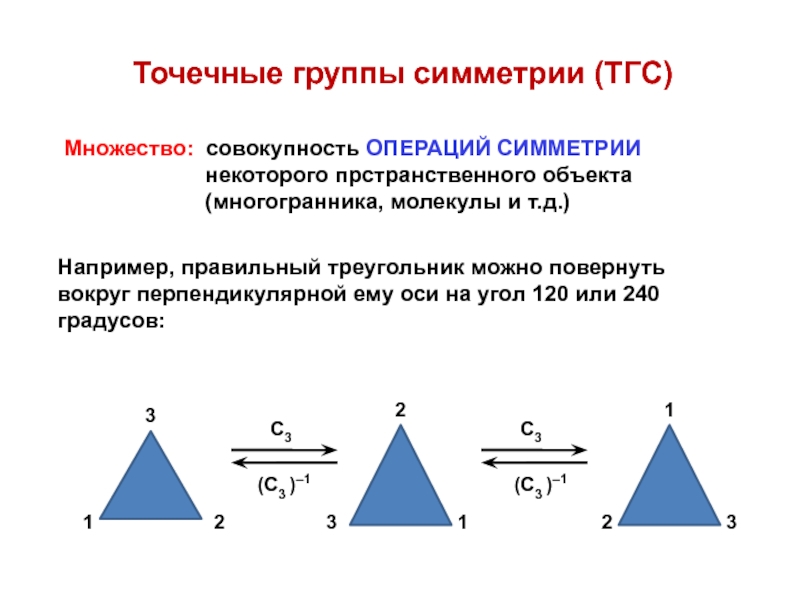
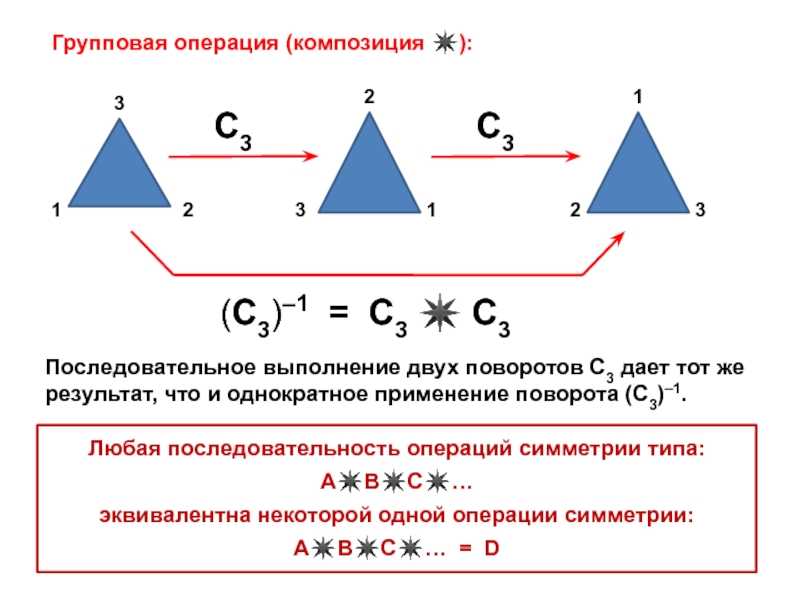
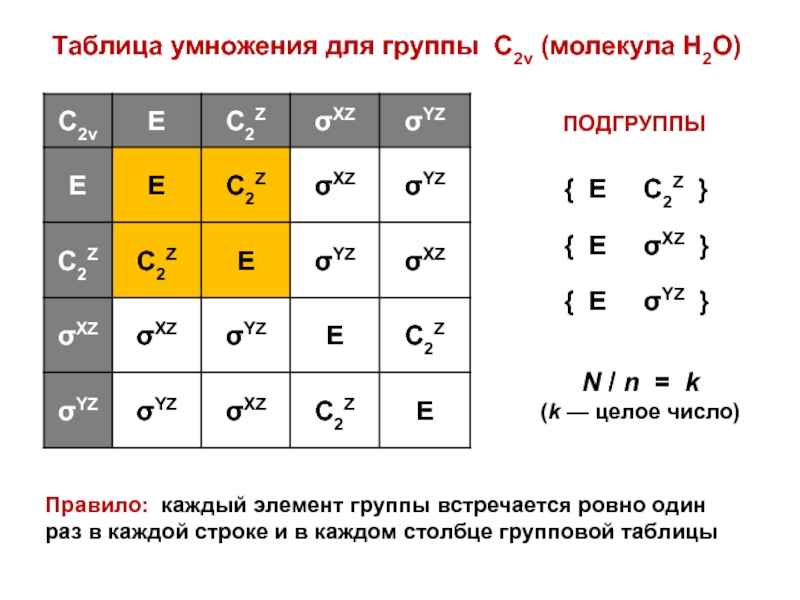

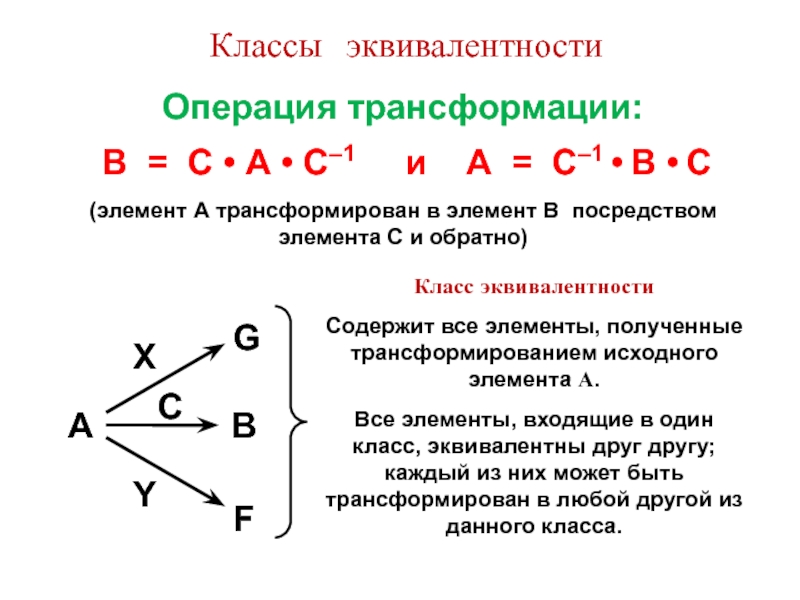
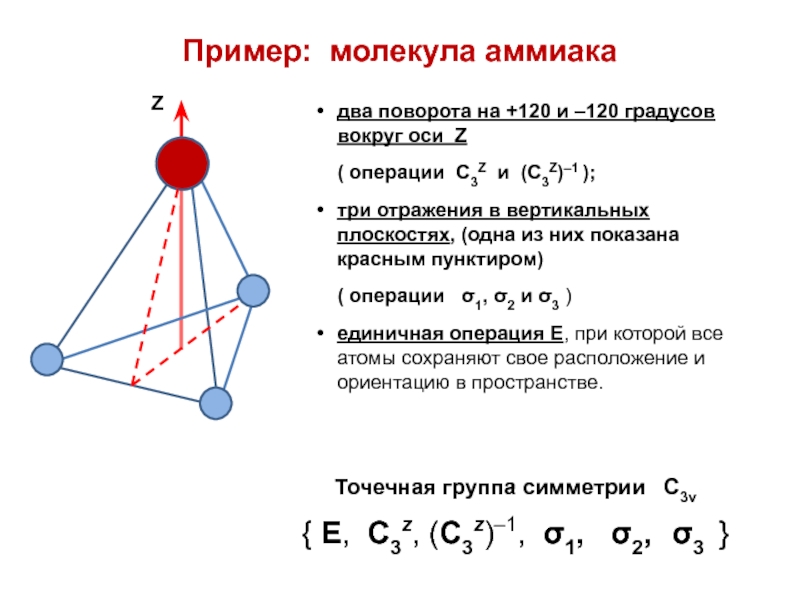

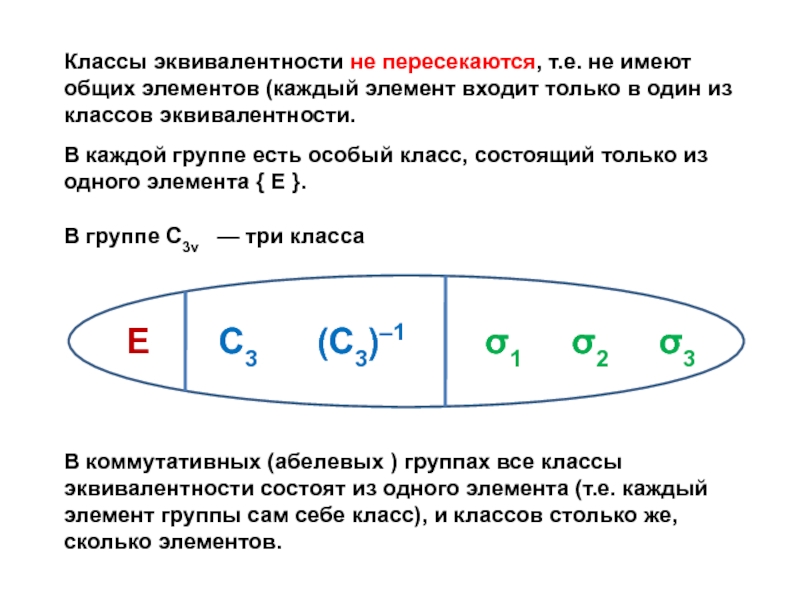
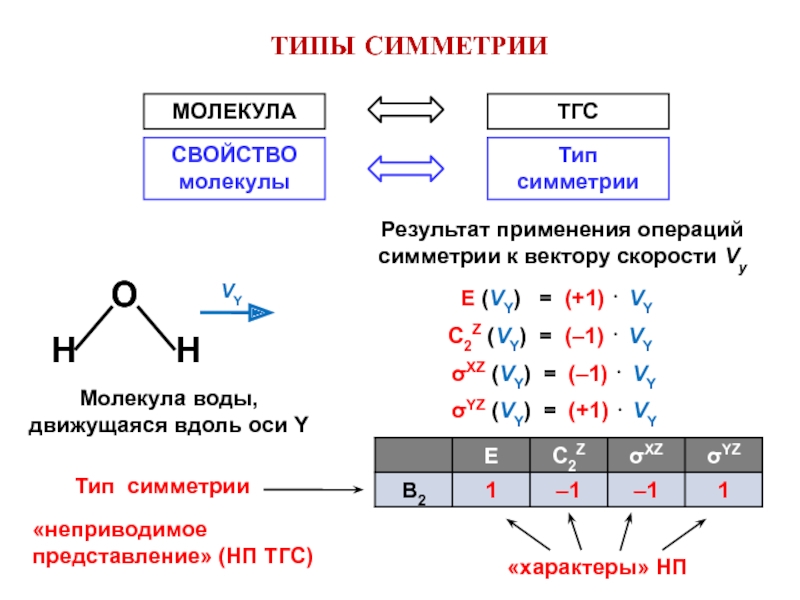



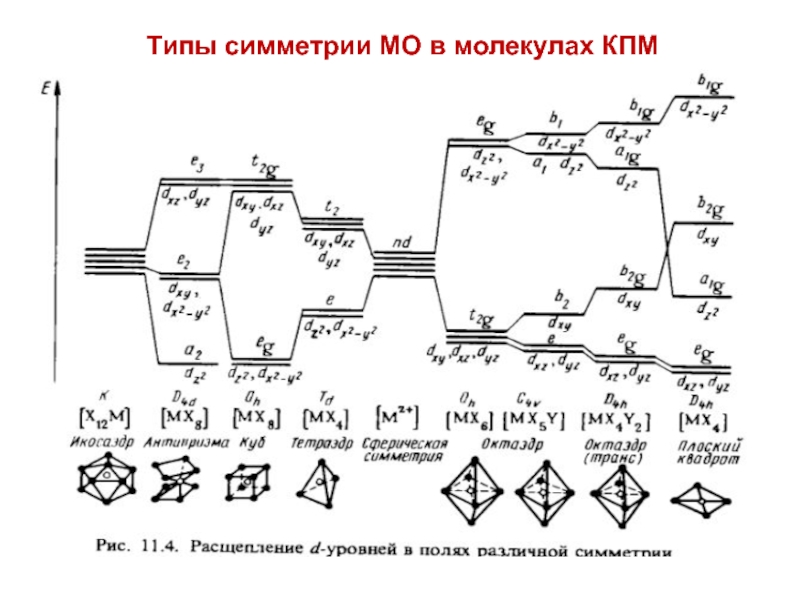
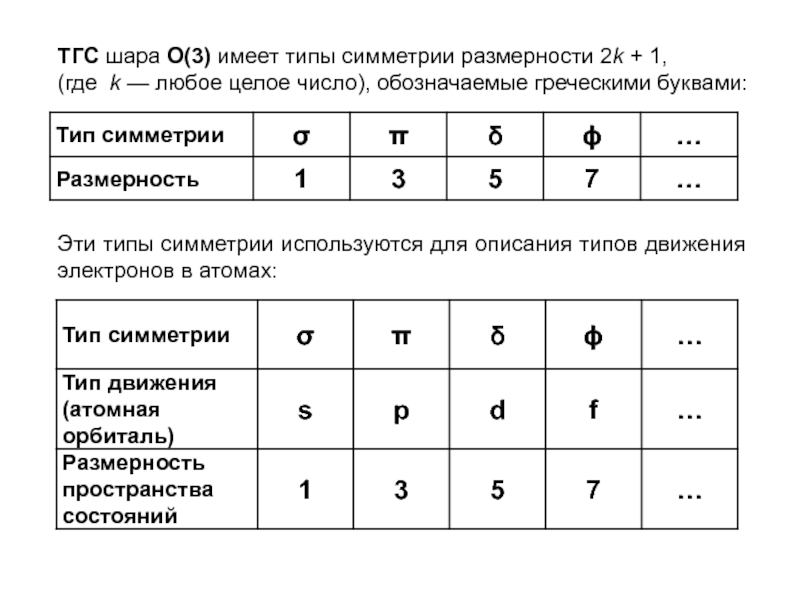









![Звуковая история Автоматизация звука [С] в прямом слоге и со стечением согласных](/img/tmb/7/638822/5f88ff8b5e1adadb4ef4610c87406b5e-800x.jpg)











