Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
16.12.19 1 Теория вероятностей и математическая статистика
Содержание
- 1. 16.12.19 1 Теория вероятностей и математическая статистика
- 2. Теория вероятностей Тема 1. Случайные события.
- 3. Теория вероятностей - раздел математики, изучающий
- 4. Литература1. Письменный Д. Конспект лекций по теории
- 5. Основные понятия теории вероятностейСобытия обозначаются обычно большими латинскими буквами A, B, D, F ...
- 6. Классификация событийДостоверное -событие, которое при повторении
- 7. Взаимосвязь событий
- 8. Взаимосвязь событий
- 9. Полная группа событий -несколько событий таких, что
- 10. События: A1
- 11. Анализ событий опыта:E - невозможное событиеF -
- 12. Алгебра событийСумма (объединение) событий А1, А2, …,Аn
- 13. Частота события и ее свойстваЕсли опыт воспроизведен
- 14. Доказательство:Пусть опыт повторен n раз, причем событие
- 15. 5) Р*(АВ)=Р*(А)Р*(В/А).Доказательство:Пусть опыт повторен n раз, событие
- 16. Частота случайного события обладает свойством устойчивости, т.е.
- 17. Вероятность события. Аксиомы теории вероятностейВероятностью Р(А) события
- 18. Классическая формулаСобытия Е1, Е2,...,Еn называются случаями в
- 19. Пример 4:Опыт - бросание игральной костиСобытие А
- 20. Пример 5:Два счета из десяти выполнены с
- 21. Основные теоремыТеорема 1. Теорема сложения вероятностей.Р(А1+А2+А3+...+Аn)= Р(А1)
- 22. Доказательство (для n=3).Р(А+В+С) = Р((А+В)+С) =
- 23. Следствие 1. Вероятность суммы двух любых событий
- 24. Замечание . Так как ,
- 25. Определение. Условной вероятностью Р(А/В) события А относительно
- 26. Доказательство Воспользуемся методом математической индукции. Р(А1А2)=Р(А1)Р(А2/А1).Предполагаем,
- 27. Следствие 1. Вероятность произведения двух любых событий
- 28. Пример 7:Студент знает ответы на 20 из
- 29. Решение. Рассмотрим события:А- студент знает ответ на
- 30. Определение.Несколько событий называют независимыми (или независимыми в
- 31. Пример 8:Два студента выполняют независимо друг от
- 32. Решение. События: А - задание выполнит первый
- 33. Пример 9: Для получения кредита предприятие обратилось
- 34. Решение. События: А - первый банк выделит
- 35. а) Т.к. D = AB
- 36. Теорема 3. Формула полной вероятностиПусть в результате
- 37. Доказательство. Р(А)=Р(А = =Р(А(Н1+Н2+...+Нn)=P(AH1+AH2+...+AHn)= /события
- 38. Пример 10:В лабораторию поступают образцы с трех
- 39. По условию Р(Н1)=50/100=0,5; Р(Н2)=30/100=0,3; Р(Н3)=20/100 = 0,2.Р(А/Н1)=0,09; Р(А/Н2)=0,1; Р(А/Н3)=0,08.Следовательно, по формуле полной вероятности Р(А)=0,50,09+0,30,1+0,20,08=0,091.Запомним
- 40. Теорема 4. Формула Байеса (теорема переоценки гипотез)Пусть
- 41. Пример 11:Пусть в предыдущем примере событие А
- 42. Теорема 5 . Формула БернуллиПроизводится n независимых
- 43. P (Xn=k) = pk
- 44. Наивероятнейшее число наступлений события при повторении испытанийЕсли
- 45. Пример 13:Найти наивероятнейшее число отказавших элементов, если
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Теория вероятностей -
раздел математики, изучающий закономерности случайных явлений,
наблюдаемых при массовых повторениях
испытаний
Слайд 4Литература
1. Письменный Д. Конспект лекций по теории вероятностей и математической
статистике. М.: Айрис-Пресс,2004.
2. Гмурман В.Е. Теория вероятностей и математическая статистика.,
М.: Высшая школа, 1977.3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979.
Слайд 5Основные понятия теории вероятностей
События обозначаются обычно большими латинскими буквами A,
B, D, F ...
Слайд 6Классификация событий
Достоверное -
событие, которое при
повторении опыта
обязательно
произойдет
обычно
обозначатся - Невозможное -событие, которое при повторениях опыта никогда не происходит
обычно обозначается
Случайное -
событие, которое при повторении опыта иногда происходит, иногда нет
обычно обозначается - A, B, C, D ...
Слайд 9Полная группа событий -
несколько событий таких, что в результате опыта
непременно должно произойти хотя бы одно из них.
Противоположные события -
2
несовместных события , образующих полную группу событийВзаимосвязь событий
Пример 1:
Опыт - бросание игральной кости
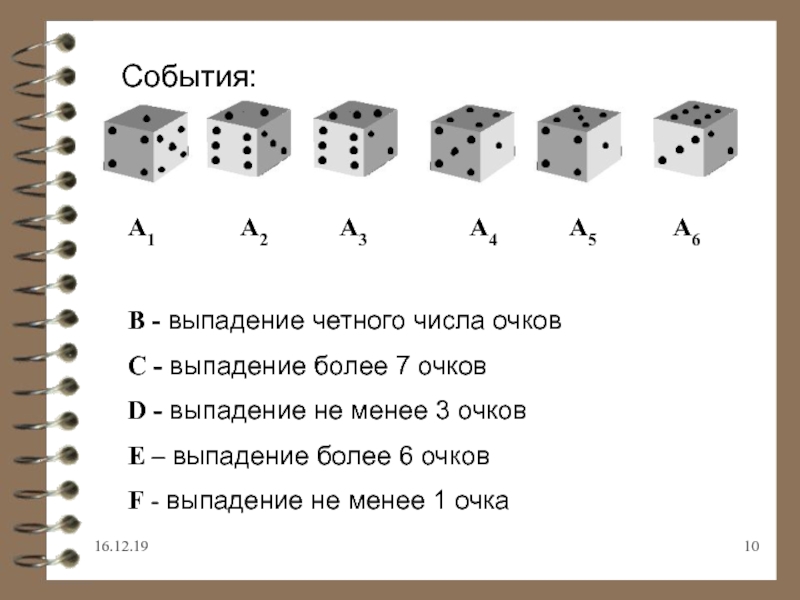
Слайд 10События:
A1
A2
A3 A4 A5 A6B - выпадение четного числа очков
C - выпадение более 7 очков
D - выпадение не менее 3 очков
E – выпадение более 6 очков
F - выпадение не менее 1 очка
Слайд 11Анализ событий опыта:
E - невозможное событие
F - достоверное событие
A1 -
A6 - элементарные события
A1 - A6 - полная группа несовместных
равновозможных событийB, C, D - можно выразить через более
простые (элементарные) события
Например:
В - наступит либо А2, либо А4, либо А6
Слайд 12Алгебра событий
Сумма (объединение) событий А1, А2, …,Аn -
событие, состоящее
в появлении хотя бы одного из этих событий
Обозначение: А1+ А2
+…+Аn = А1 А2 … АnПроизведение (пересечение) событий А1, А2, …,Аn -
событие, состоящее в появлении всех этих событий
Обозначение: А1·А2 · … ·Аn = А1 А2 … Аn
Слайд 13 Частота события и ее свойства
Если опыт воспроизведен n раз, а
событие А произошло m раз, то частотой (относительной частотой) события
А назовемР*(А)=
т.е. отношение числа испытаний, в которых появилось событие А, к числу всех испытаний.
Свойства частоты.
1) 0< Р*(А) < 1, так как 0< m< n, следовательно,
2) Р*()=1, так как m=n.
3) Р*()=0, так как m=0.
4) Р*(А+В)=Р*(А)+Р*(В)-Р*(АВ).
Слайд 14Доказательство:
Пусть опыт повторен n раз, причем событие А появилось m1
раз, событие В появилось m2 раза, вместе А и В
появились при этом m3 раза. ТогдаСлайд 155) Р*(АВ)=Р*(А)Р*(В/А).
Доказательство:
Пусть опыт повторен n раз, событие А при этом
появилось m1 раз, событие В появилось m2 раза, вместе А
и В появились m3 раза. ТогдаАналогично, можно доказать, что Р*(АВ)=Р*(В)Р*(А/В).
Слайд 16Частота случайного события обладает свойством устойчивости, т.е. при увеличении числа
опытов значения частоты события группируются около некоторого числа, характеризующего возможность
появления данного события в данном опыте.Таким образом, мы приходим к понятию вероятности события в данном опыте.
Слайд 17 Вероятность события. Аксиомы теории вероятностей
Вероятностью Р(А) события А в опыте
назовем численную меру объективной возможности появления события А в данном
опыте.Основные аксиомы:
Аксиома1. Вероятность любого события А есть число Р(А), удовлетворяющее неравенствам 0
Аксиома 2. Вероятность достоверного события равна единице, т.е. Р()=1.
Аксиома 3. Вероятность невозможного события равна нулю, т.е. Р()=0.
Слайд 18Классическая формула
События Е1, Е2,...,Еn называются случаями в опыте, если
они
образуют полную группу событий, т.е. Е1+Е2+...+Еn=;
несовместны, т.е. ЕiEj=, где ij;
равновозможны.
Случай называется благоприятным событию А, если появление этого случая влечет появление события А. Пусть в данном опыте благоприятными событию А являются случаи Е1, Е2,...,Еm, т.е. А= Е1 + Е2 +... + Еm, тогда
где m - число благоприятных событию А случаев, n - число всех случаев в данном опыте.
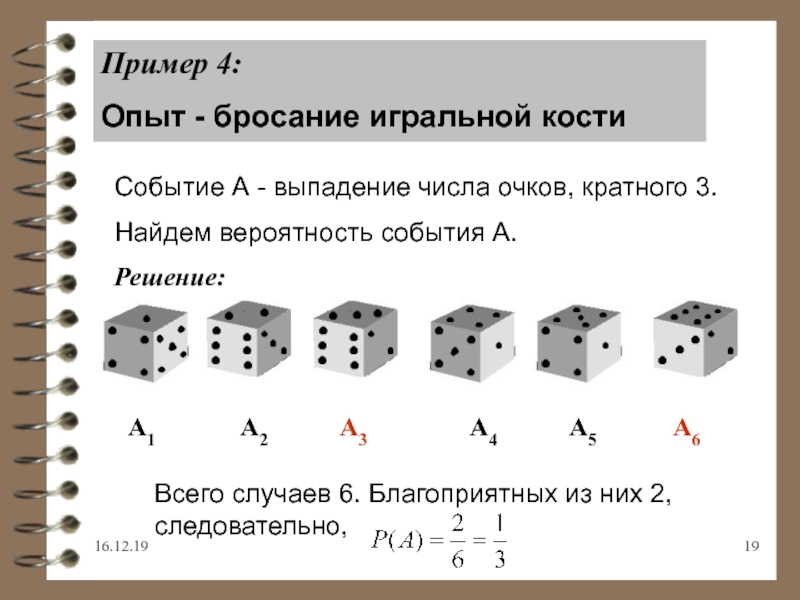
Слайд 19Пример 4:
Опыт - бросание игральной кости
Событие А - выпадение числа
очков, кратного 3.
Найдем вероятность события А.
Решение:
A1
A2 A3 A4 A5 A6Всего случаев 6. Благоприятных из них 2, следовательно,
Слайд 20Пример 5:
Два счета из десяти выполнены с ошибками. Найти вероятность
того, что из четырех взятых на проверку счетов один счет
окажется с ошибкамиРешение:
Имеем дело с неупорядоченными выборками без повторений, следовательно, всего случаев n=С104,
благоприятных из них m=С21С83.
Следовательно
= = =
Слайд 21Основные теоремы
Теорема 1. Теорема сложения вероятностей.
Р(А1+А2+А3+...+Аn)= Р(А1) + Р(А2) +
Р(А3) + ... + Р(Аn) - Р(А1А2) - Р(А1А3) -
Р(A2A3) -...- - P(An-1An) + P(A1A2A3) + P(A1A2A4) +...+ + P(An-2An-1An) -...++(-1)n-1 P(A1A2...An).
Слайд 22 Доказательство (для n=3).
Р(А+В+С) = Р((А+В)+С) = / по аксиоме
4 / = Р(А+В)+Р(С)-Р((А+В)С) = Р(А+В) + Р(С) - Р(АС+ВС)
= Р(А+В) + Р(С) - (Р(АС) + Р(ВС) - Р(АВС)) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС)- Р(ВС) + Р(АВС).Следствие.
Если события А1, А2, ... ,Аn несовместны,
то
Р(А1+А2+...+Аn)=P(A1)+P(A2)+...+P(An).
Слайд 23Следствие 1. Вероятность суммы двух любых событий равна сумме вероятностей
этих событий без вероятности их произведения, т.е.
Р(А+В)=Р(А)+Р(В)-Р(АВ).
Следствие 2. Если
события А и В несовместны, то АВ= и следовательно, Р(А+В)=Р(А)+Р(В).
Следствие 2. Если события А1, А2, ... ,Аn несовместны, то
Р(А1+А2+...+Аn)=P(A1)+P(A2)+...+P(An).
Слайд 25Определение. Условной вероятностью Р(А/В) события А относительно события В назовем
вероятность события А при условии, что событие В уже произошло.
Теорема
2. Теорема умножения вероятностей.Р(А1А2А3...Аn) = Р(А1)Р(А2/А1)Р(А3/А1А2) … Р(Аn/А1А2А3...Аn-1).
Слайд 26 Доказательство
Воспользуемся методом математической индукции.
Р(А1А2)=Р(А1)Р(А2/А1).
Предполагаем, что теорема верна
для (n-1) событий; докажем, что она верна для n событий.
Найдем
Р(А1А2А3...Аn)=P((A1A2A3...An-1)An) = =P(A1A2A3...An-1)P(An/A1A2A3...An-1) = / по предположению /= P(A1)P(A2/A1) P(A3/A1A2) ..P(An-1/A1A2A3An-2)P(An/A1A2A3...An-1).Слайд 27Следствие 1. Вероятность произведения двух любых событий равна произведению вероятности
одного из них на условную вероятность другого относительно первого, т.е.
Р(АВ)=Р(А)Р(В/А)=Р(В)Р(А/В).
Событие А называется независимым от события В, если условная вероятность события А относительно события В равна безусловной вероятности события А, т.е. Р(А/В)=Р(А). Нетрудно доказать, что если А не зависит от В, то и В не зависит от А.
Следствие 2. Если события А и В независимы, то
Р(АВ)=Р(А)Р(В).
Слайд 28Пример 7:
Студент знает ответы на 20 из 25 вопросов. Какова
вероятность того, что он ответит на два выбранных наудачу вопроса?
Слайд 29Решение.
Рассмотрим события:
А- студент знает ответ на первый вопрос,
В-
студент знает ответ на второй вопрос.
Найдем Р(АВ).
Р(АВ) = Р(А)Р(В/А) =
Слайд 30Определение.
Несколько событий называют независимыми
(или независимыми в совокупности),
если независимы
каждые два из них и
независимы каждое событие и все
возможные произведения остальных.Следовательно, если А1, А2, ... ,Аn независимы, то Р(А2/А1) = Р(А2), Р(А3/А1А2) = Р(А3), ... , Р(Аn/A1A2A3...An-1) = P(An), тогда
Р(А1A2A3...An)=P(A1)P(A2)P(A3)...P(An).
Слайд 31Пример 8:
Два студента выполняют независимо друг от друга задание. Вероятность
того, что задание будет выполнено первым студентом 0,6;
для второго
студента эта вероятность равна 0,8. Найти вероятность того, что
1) оба студента выполнят задание;
2) только один из них выполнит задание;
3) хотя бы один из них выполнит задание.
Слайд 32Решение.
События: А - задание выполнит первый студент,
В - задание
выполнит второй студент.
По условию Р(А) = р1 = 0,6;
Р(В)=р2 = 0,8; следовательно, Р( ) = 1-p1 = q1 = 1-0,6 = 0,4; P( ) = 1-p2 = q2 = 1-0,8 = 0,2.Р(АВ) = /события А и В - независимые события / = Р(А)Р(В) = р1р2 =0,60,8 = 0,48.
Р(А + B) = / A и B - несовместные события /= Р(А ) + Р( В) = Р(А)Р( ) +
Р( )Р(В) = p1q2+q1p2 = 0,60,2 + 0,40,8 = 0,44.
P(A+B)=/ А и В - совместные события /= Р(А)+Р(В)-Р(АВ)=0,6+0,8-0,48=0,92
или т.к. А+В и противоположные события, то
Р(А+В)=1-Р( )= 1 - Р( )Р( ) = 1-q1q2 = 1-0,40,2 = 1-0,08 = 0,92.
Слайд 33Пример 9:
Для получения кредита предприятие обратилось к трем банкам.
Статистические исследования показали, что вероятности выделения кредита этими банками соответственно
равны р1=0,5, р2=0,4 и р3=0,9. Банки выделяют кредит независимо друг от друга и, если примут решение о его выделении, то в размере: первый банк-160 тыс. руб., второй-40 тыс. руб., третий-200 тыс. руб.Найти вероятности того, что предприятие получит кредит
а) в размере 200 тыс. руб.,
б) не менее 240 тыс. руб.
с) в любом размере.
Слайд 34Решение.
События:
А - первый банк выделит кредит,
В -
второй банк выделит кредит,
С - третий банк выделит кредит,
D - предприятие получит кредит в размере 200 тыс. руб.,
E - предприятие получит кредит в размере не менее 240 тыс. руб.,
F – получит кредит.
Слайд 35а) Т.к. D = AB
,
то P(D) = 0,50,4(1 - 0,9) + (1 - 0,5)(1 - 0,4)0,9 = 0,02 + 0,27 = 0,29.
б)Т.к.E=A ,
то P(E)=0,5(1-0,4)0,9+(1-0,5)0,40,9+0,50,40,9=0,63.
с) , то P(F) = 1 – P( F ) = 1 – 0 ,5 0,6 0,1= 0,97.
Слайд 36Теорема 3. Формула полной вероятности
Пусть в результате опыта может появиться
какое-либо из несовместных событий Н1,Н2,...,Нn, образующих полную группу. Событие А
может появиться только вместе с одним из этих событий. События Н1, Н2,..., Нn называются гипотезами.Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А/Нi), где i = , то
Слайд 37Доказательство.
Р(А)=Р(А = =Р(А(Н1+Н2+...+Нn)=P(AH1+AH2+...+AHn)=
/события AHi и AHj,
где несовместные события, т.к.
(AHi)(AHj)=AHiHj=A(HiHj)=A = /= Р(АН1)+Р(АН2)+...+Р(АНn)=
=P(H1)P(A/H1)+P(H2)P(A/H2)+...+P(Hn)P(A/Hn).
Слайд 38Пример 10:
В лабораторию поступают образцы с трех баз, причем 50%
с первой базы,30% со второй базы, остальные с третьей базы.
Вероятность того, что образец c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу образец окажется бракованным.Решение.
Рассмотрим гипотезы:
Н1 -взятый образец поступил с первой базы,
Н2 -взятый образец поступил со второй базы,
Н3 -взятый образец поступил с третьей базы.
Событие А - образец окажется бракованным.
Слайд 39По условию
Р(Н1)=50/100=0,5;
Р(Н2)=30/100=0,3;
Р(Н3)=20/100 = 0,2.
Р(А/Н1)=0,09;
Р(А/Н2)=0,1;
Р(А/Н3)=0,08.
Следовательно, по
формуле полной вероятности
Р(А)=0,50,09+0,30,1+0,20,08=0,091.
Запомним
Слайд 40Теорема 4. Формула Байеса
(теорема переоценки гипотез)
Пусть в условиях предыдущей
теоремы событие А наступило и мы нашли вероятность Р(А). Спросим,
как изменились вероятности гипотез в связи с появлением события А, т.е. найдем Р(Нi/А), где i=1,2,...,n.Слайд 41Пример 11:
Пусть в предыдущем примере событие А наступило, т.е. взятый
наудачу образец оказался бракованным. Определить вероятность того, что этот образец
поступил со второй базы.Решение.
Р(Н2/А) =
Слайд 42Теорема 5 . Формула Бернулли
Производится n независимых испытаний, в каждом
из которых событие А наступает с постоянной вероятностью р. Найдем
вероятность того, что в этих n испытаниях событие А появится ровно k раз, т.е. найдем P (Xn=k).Слайд 43P (Xn=k) = pk qn-k, где q=1-p
Пример
12:
Каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4.
Найти вероятность того, что откажут три элемента из пяти.Решение.
Р5(3)= р3q2= 0,430,62 =
=100,0640,36=0,23.
Слайд 44Наивероятнейшее число наступлений события при повторении испытаний
Если k0 - наивероятнейшее
число появления события А в n независимых испытаниях, в каждом
из которых событие А наступает с постоянной вероятностью рnp-q < k0 < np+p.
Слайд 45Пример 13:
Найти наивероятнейшее число отказавших элементов, если каждый из пяти
независимо работающих элементов отказывает с вероятностью 0,4.
Решение.
Так как n=5,
p=0,4, q=0,6, то 50,4-0,6 k0 < 50,4+0,4 или
1,4 < k0 < 2,4. Следовательно, k0=2.