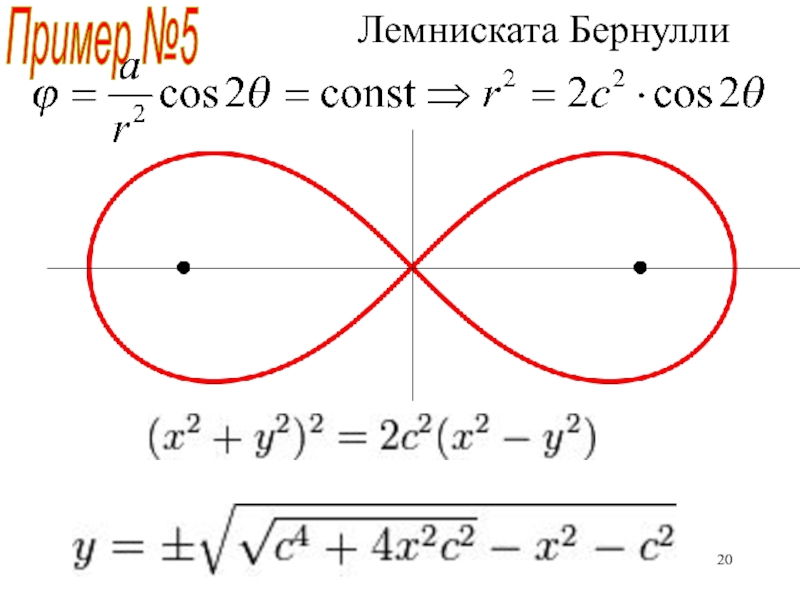
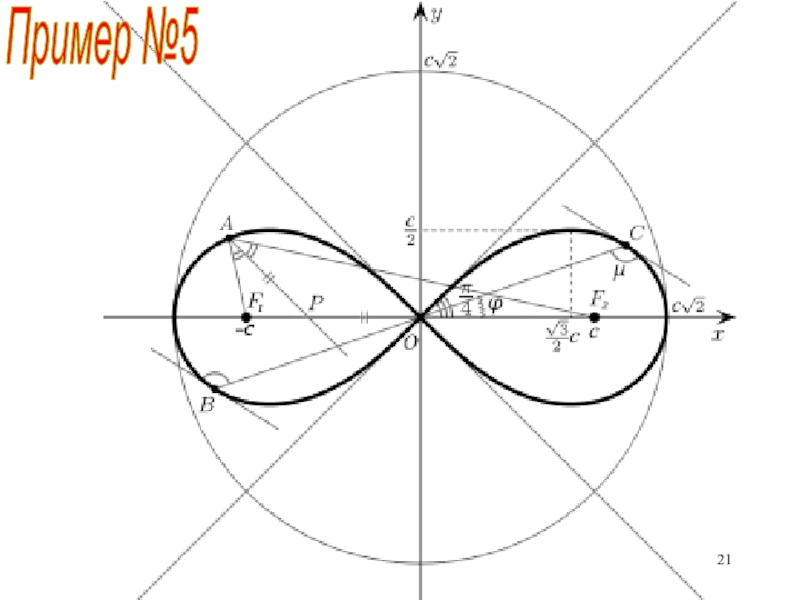
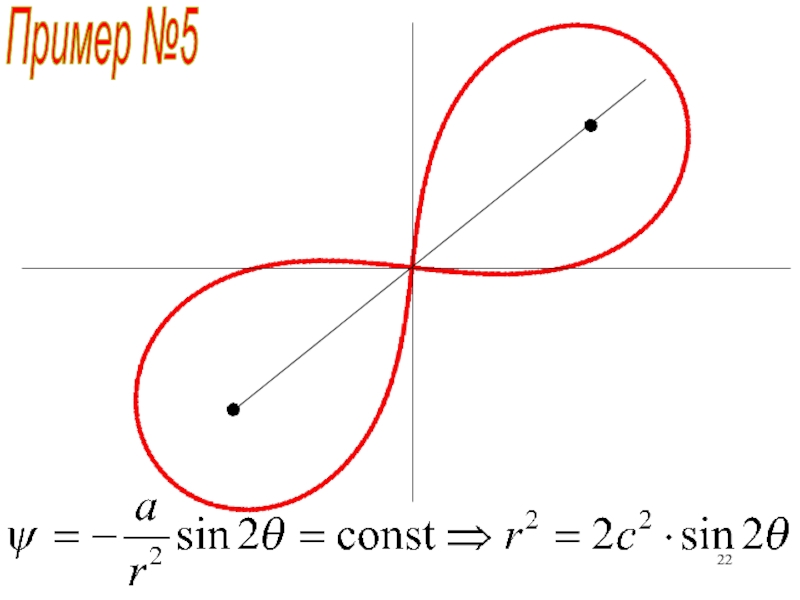
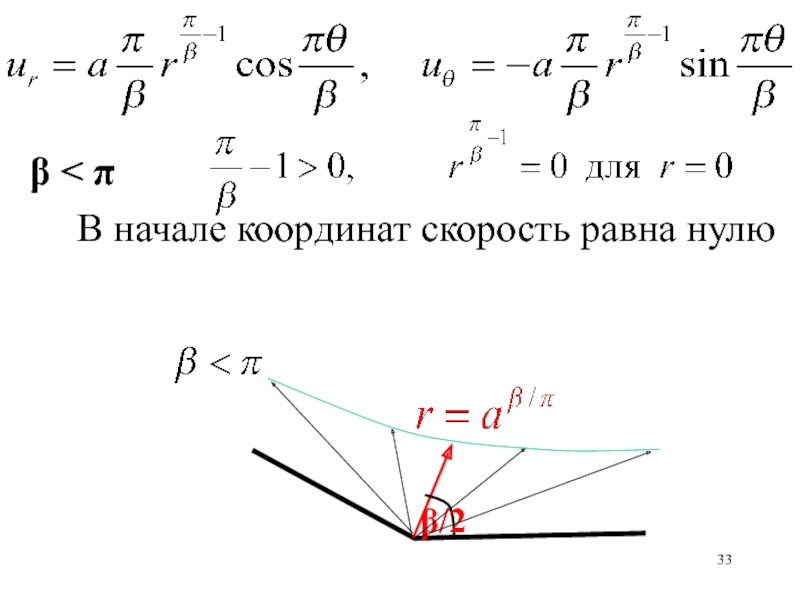
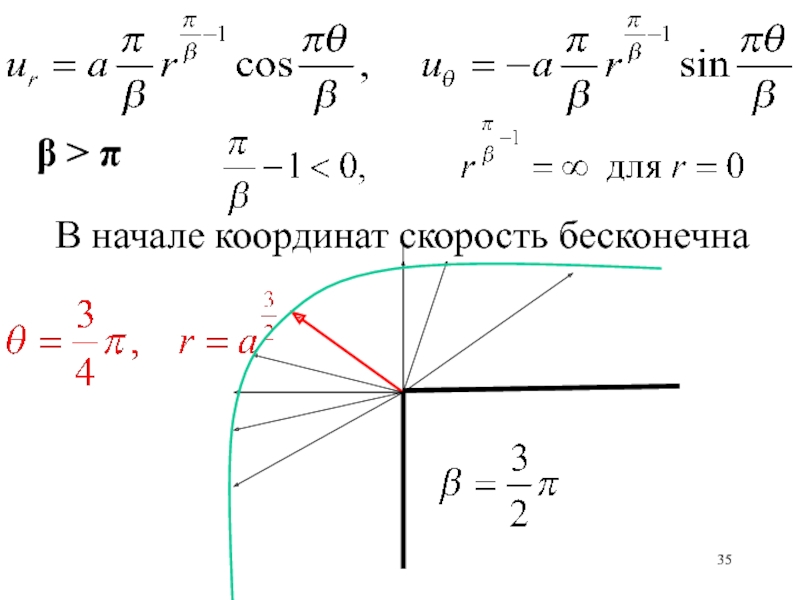
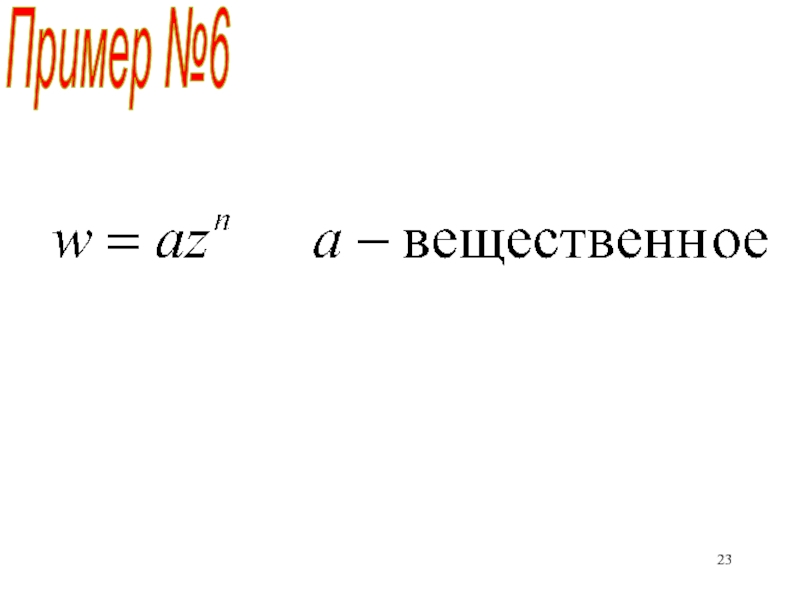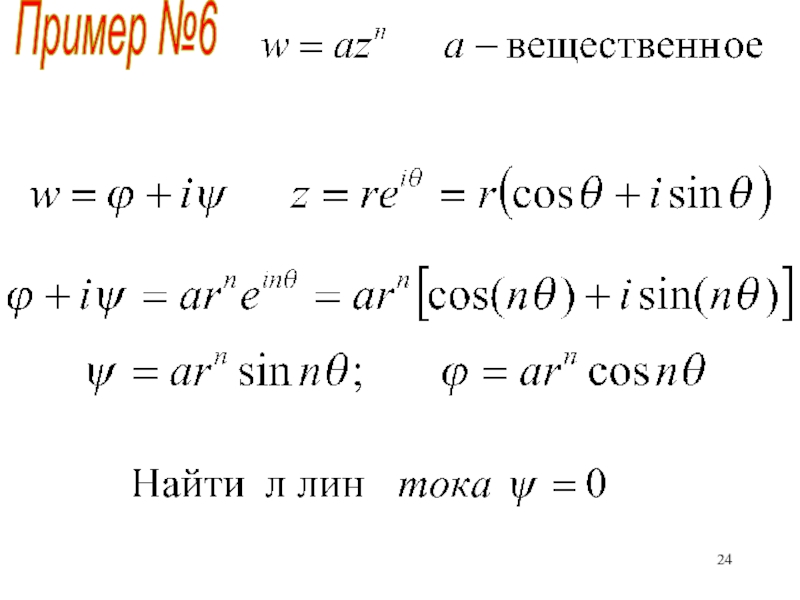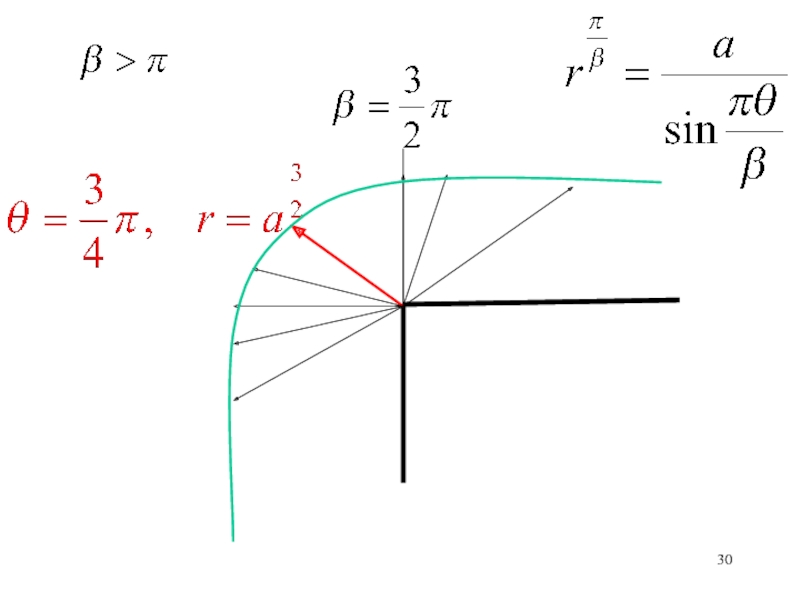неравномерного прогрева Солнцем поверхности Земли)
Записать уравнение Гельмгольца, раскрыв полную производную
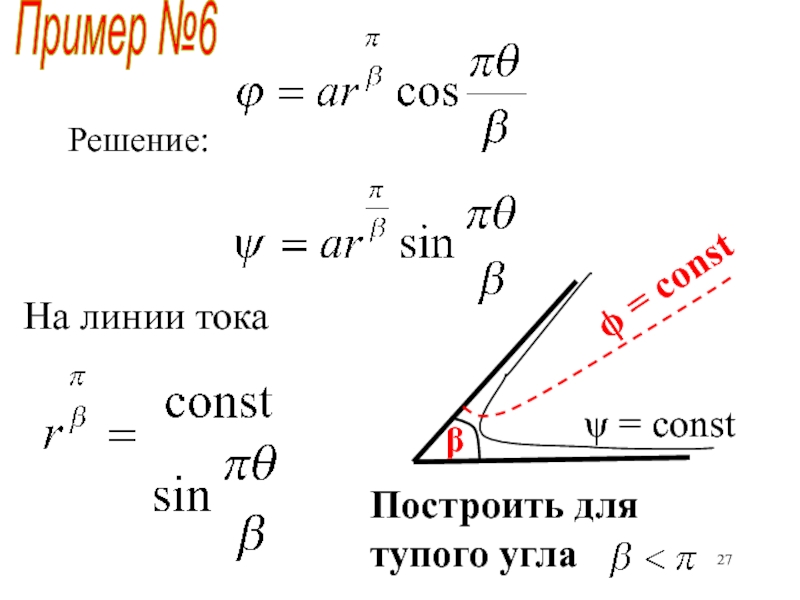
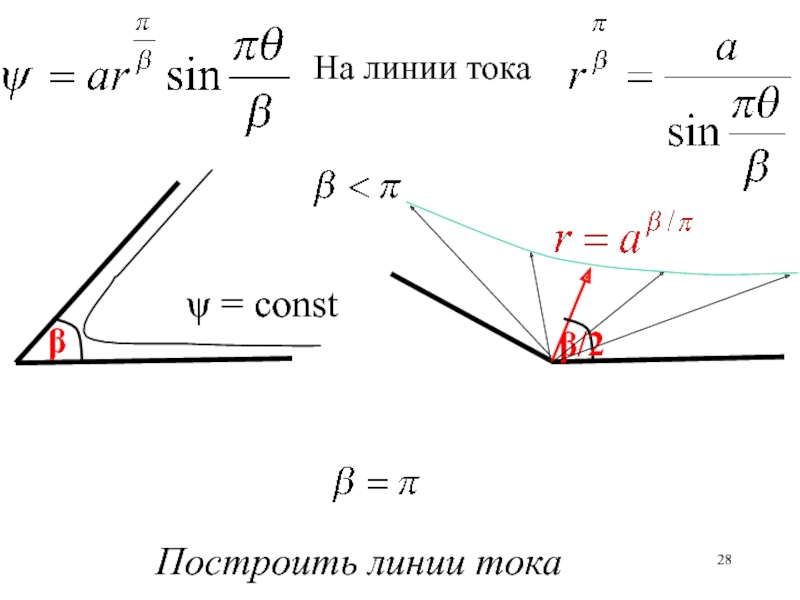
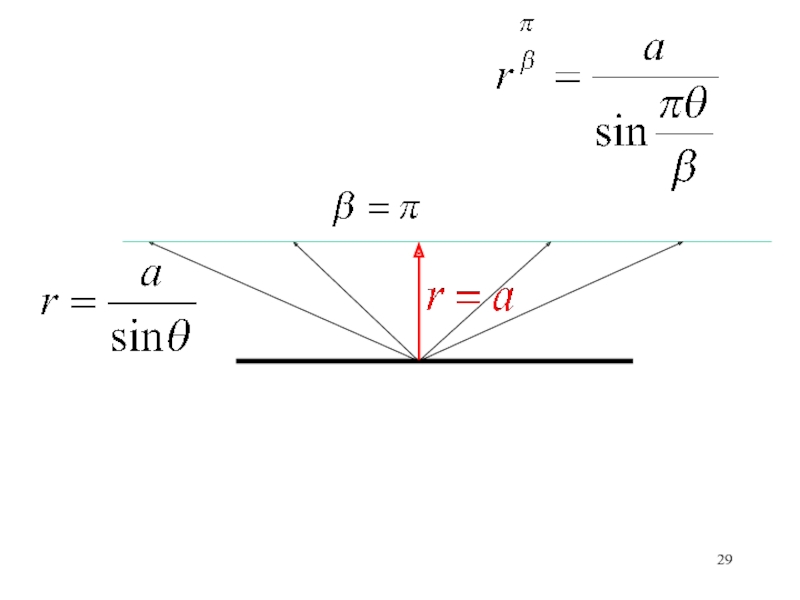
по времени. При каких условиях оно существует.Уравнения Эйлера, неразрывности, линии тока, Бернулли-Эйлера, Фридмана










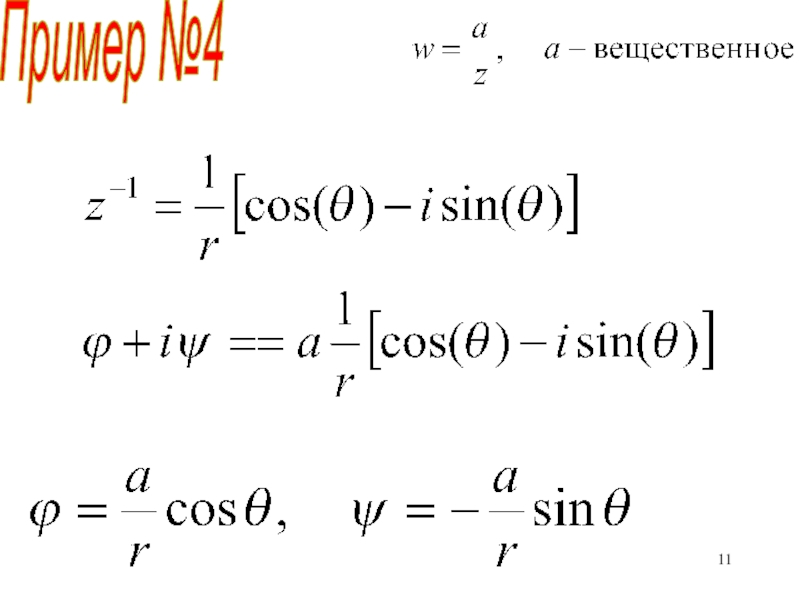

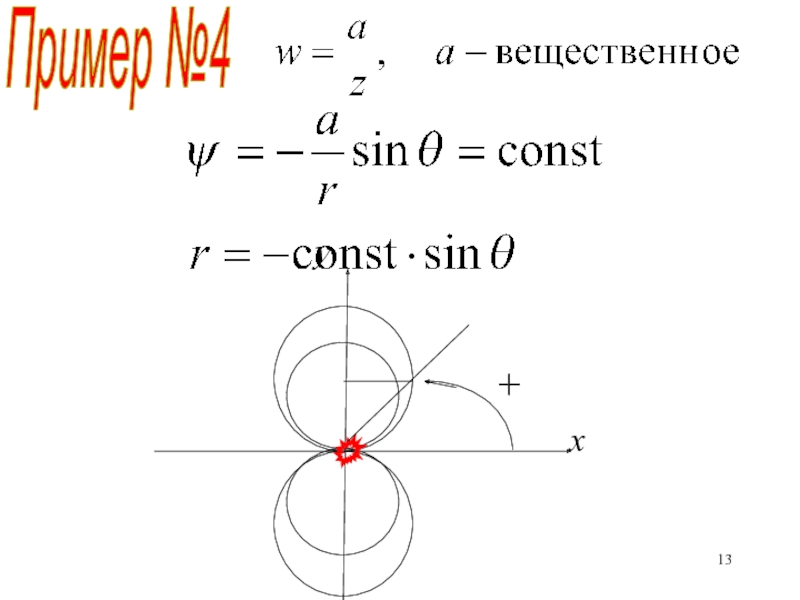


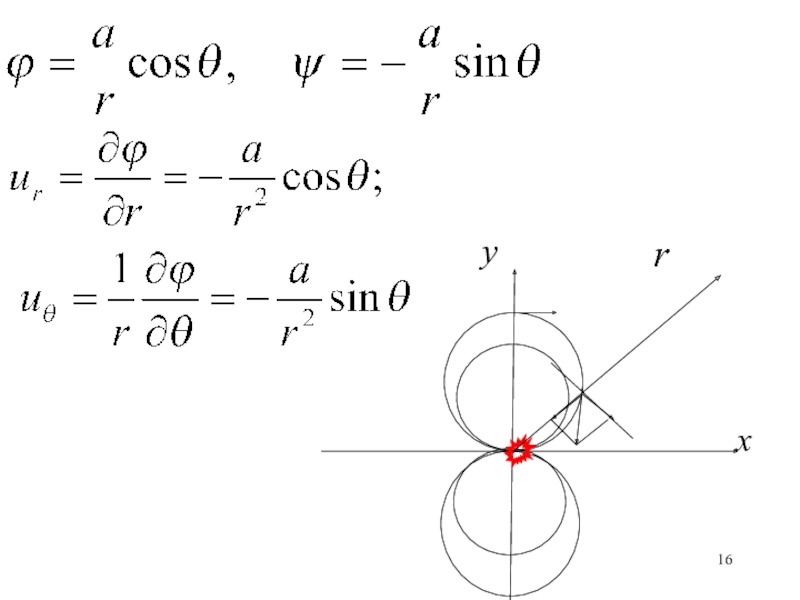
![1
Эйлер, Ляпунов, Навье и Стокс Пример №4Определить поток через отрезок [(0, i), (0, -i)] Пример №4Определить поток через отрезок [(0, i), (0, -i)]](/img/thumbs/0a61210eca2136b95e630f3ee31a8351-800x.jpg)