Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Лекция № 15 (сем. 1) Неинерциальные системы отсчёта План лекции: 1. Понятие о
Содержание
- 1. 1 Лекция № 15 (сем. 1) Неинерциальные системы отсчёта План лекции: 1. Понятие о
- 2. 1. Понятие о неинерциальных системах отсчёта В
- 3. 1. Понятие о неинерциальных системах отсчёта Если
- 4. Из рисунка видно, что радиусы-векторы частицы т
- 5. Основное свойство неинерциальных систем состоит в том,
- 6. 2. Силы инерции Силы инерции – это силы,
- 7. 2. Силы инерции Виды сил инерции и их
- 8. 3. Кориолисово ускорение
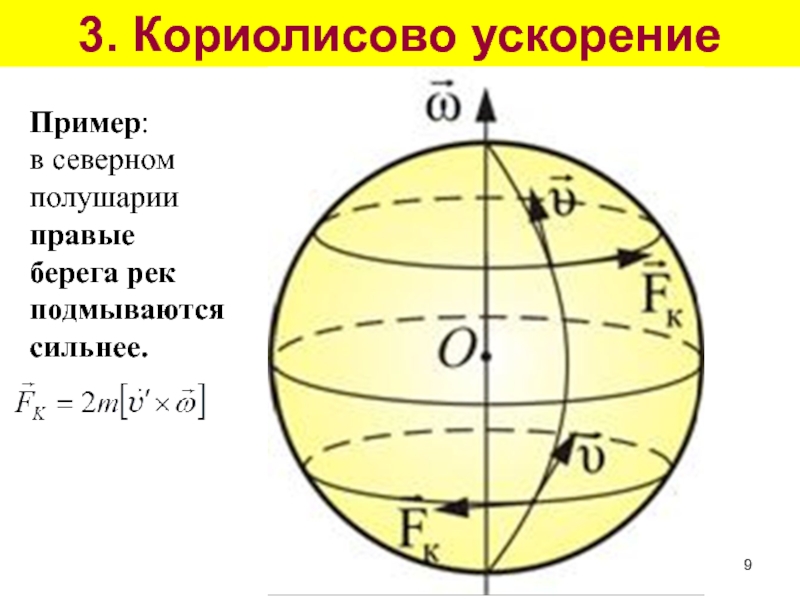
- 9. 3. Кориолисово ускорение Пример: в северном полушарии правые берега рек подмываются сильнее.
- 10. 2.3. Кориолисово ускорение
- 11. Основной закон динамики для неинерциальных систем отсчёта (НИСО) _ _ _ _ _Далее – интернет-тесты
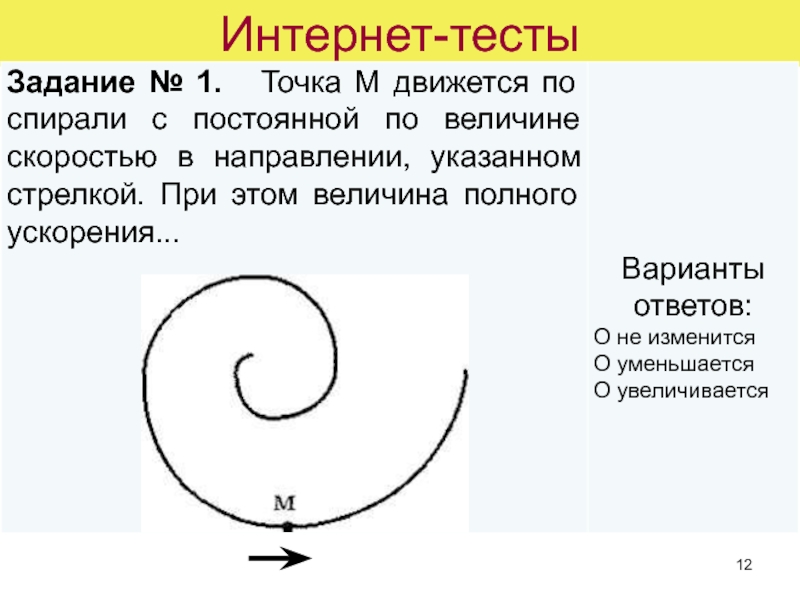
- 12. Интернет-тесты
- 13. Интернет-тестыЗадание № 2. Материальная точка М
- 14. Интернет-тестыЗадание № 3. Частица движется вдоль
- 15. Интернет-тестыЗадание № 4. Обруч массой m=0,3
- 16. Интернет-тестыЗадание № 5. Планета массой m
- 17. Интернет-тестыЗадание № 6. На рисунке представлен
- 18. Интернет-тесты
- 19. Интернет-тесты_ _ _ _ _
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция № 15 (сем. 1)
Неинерциальные системы отсчёта
План лекции:
1. Понятие о неинерциальных
системах отсчёта.
Интернет-тесты.Слайд 21. Понятие о неинерциальных системах отсчёта
В предыдущих разделах рассматривался
и использовался лишь класс инерциальных систем отсчета.
Выделяется этот класс,
прежде всего тем, что в таких системах можно описывать движение с помощью законов классической динамики. Кроме того, пространство в таких системах обладает свойствами однородности и изотропности.
Опишем движение в неинерциальных системах отсчета (НИСО) и посмотрим, что изменяется при этом по сравнению со случаем инерциальных систем.
Слайд 31. Понятие о неинерциальных системах отсчёта
Если радиус-вектор частицы в
системе К обозначить , то в силу инерциальности
системы мы можем записать второй закон Ньютона:.
Пусть теперь у нас есть неинерциальная система отсчета К', начало координат которой движется по отношению к системе К по некоторому нелинейному закону , где — радиус-вектор начала 0' в системе К (см. рисунок).
Пусть имеется частица массой m, на которую действует некоторая сила F. Выберем условно неподвижную инерциальную систему отсчета К.
Слайд 4 Из рисунка видно, что радиусы-векторы частицы т в инерциальной (
) и неинерциальной ( ) системах связаны
равенством: .Продифференцируем дважды это равенство по времени, считая время одним и тем же в системах К и К'. Тогда
Сила F, действующая на частицу, не может измениться от того, что мы перейдем в другую систему отсчета, а ускорение, как это видно из последнего уравнения, меняется, так как система К' неинерциальна, и .
Следовательно, , т. е. второй закон Ньютона, используемый для инерциальных систем, не действует и требует корректировки. Это несоответствие обусловлено тем, что в неинерциальной системе К' существует поле ускорений, не связанное с действующей силой F.
1. Понятие о неинерциальных системах отсчёта
Слайд 5 Основное свойство неинерциальных систем состоит в том, что в этих
системах существуют поля ускорений.
Закон Ньютона для неинерциальных
систем отсчета:
где
– силы инерции.Силы при этом должны быть такими, чтобы вместе с силами , обусловленными воздействием тел друг на друга, они сообщали телу ускорение , каким оно обладает в неинерциальных системах отсчета.
( ( — ускорение тела в инерциальной системе отсчета)).
1. Понятие о неинерциальных системах отсчёта
Слайд 62. Силы инерции
Силы инерции – это силы, обусловленные ускоренным движением
системы отсчета, относительно измеряемой системы отсчета.
Силы инерции вызываются не взаимодействием
тел, а ускоренным движением системы отсчета.Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу.
Слайд 72. Силы инерции
Виды сил инерции и их проявления
1. Силы инерции
при ускоренном поступательном движении системы отсчёта:
Пример: они проявляются в
перегрузках при запуске и спуске космических кораблей.2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета:
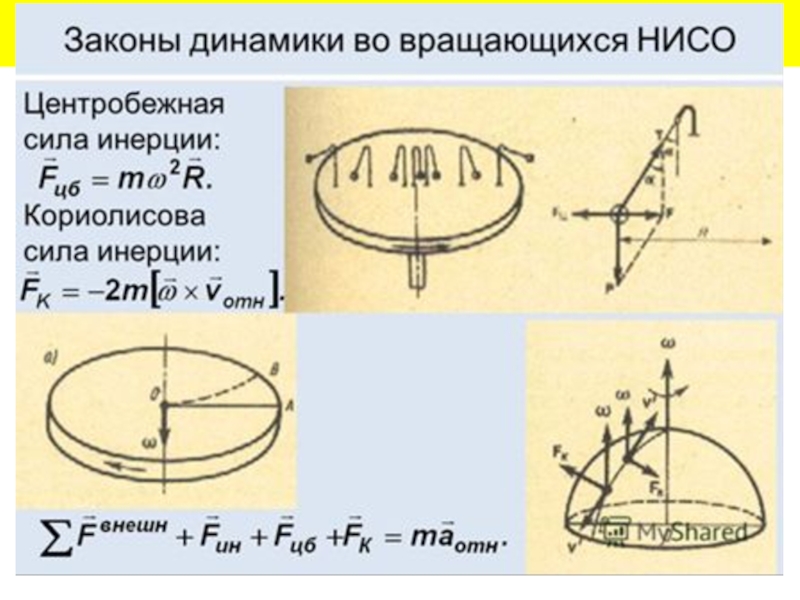
Сила — центробежная сила инерции, направленная от оси вращения системы вдоль радиуса вращение,
— угловая скорость.
Пример: их действию подвергаются пассажиры в движущемся транспорте на поворотах.
Слайд 11Основной закон динамики для неинерциальных систем отсчёта (НИСО)
_ _
_ _ _
Далее – интернет-тесты
Слайд 13Интернет-тесты
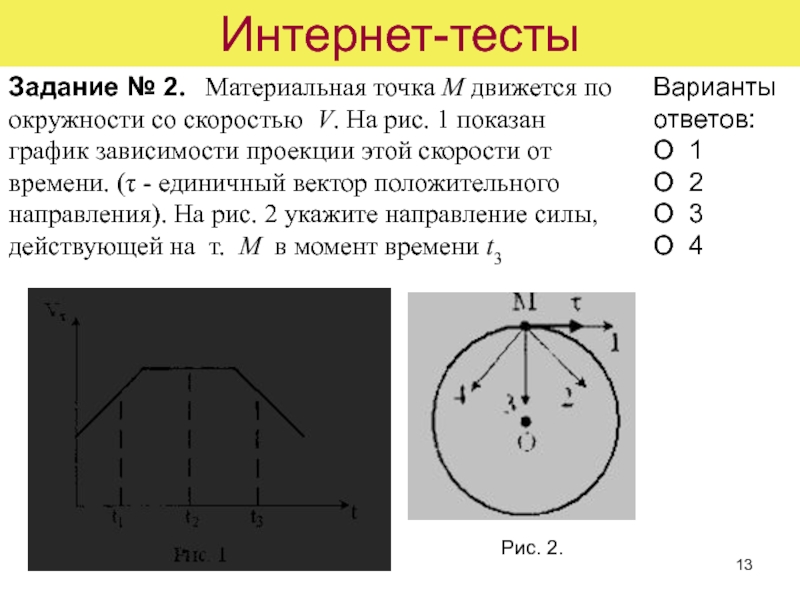
Задание № 2. Материальная точка М движется по окружности
со скоростью V. На рис. 1 показан график зависимости проекции
этой скорости от времени. (τ - единичный вектор положительного направления). На рис. 2 укажите направление силы, действующей на т. М в момент времени t3Рис. 2.
Варианты ответов:
O 1
O 2
O 3
O 4
Слайд 14Интернет-тесты
Задание № 3. Частица движется вдоль окружности радиусом 1
м в соответствии с уравнением
, где φ в радианах, t в секундах. Частица остановится в момент времени (в секундах), равный...Варианты ответов:
O 1
O 2
O 3
O 4
Слайд 15Интернет-тесты
Задание № 4. Обруч массой m=0,3 кг и радиусом
R=0,5 м привели во вращение, сообщив ему энергию вращательного движения
1200 Дж, и опустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Если обруч начал двигаться без проскальзывания, имея кинетическую энергию поступательного движения 300 Дж, то сила трения совершила работу, равную...Варианты ответов:
O 600 Дж
O 800 Дж
O 1000 Дж
O 1400 Дж
Слайд 16Интернет-тесты
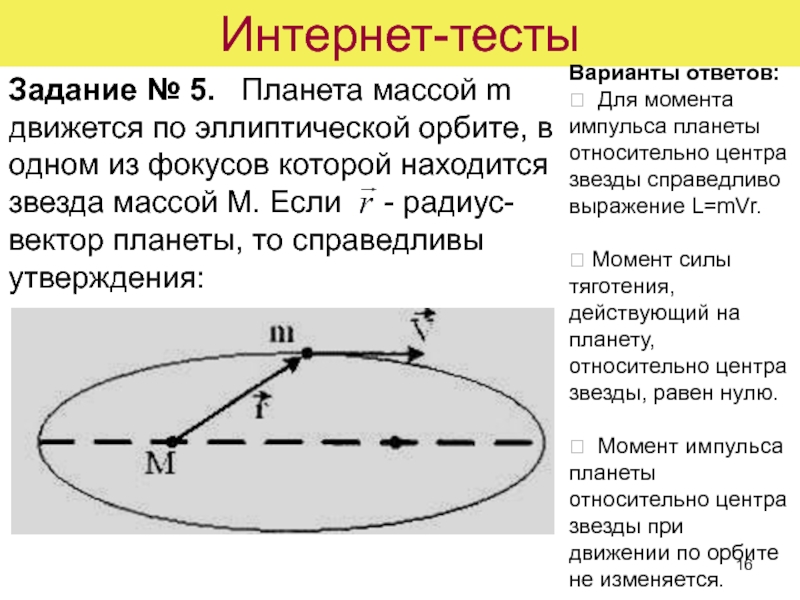
Задание № 5. Планета массой m движется по эллиптической
орбите, в одном из фокусов которой находится звезда массой М.
Если - радиус-вектор планеты, то справедливы утверждения:Варианты ответов:
Для момента импульса планеты относительно центра звезды справедливо выражение L=mVr.
Момент силы тяготения, действующий на планету, относительно центра звезды, равен нулю.
Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
Слайд 17Интернет-тесты
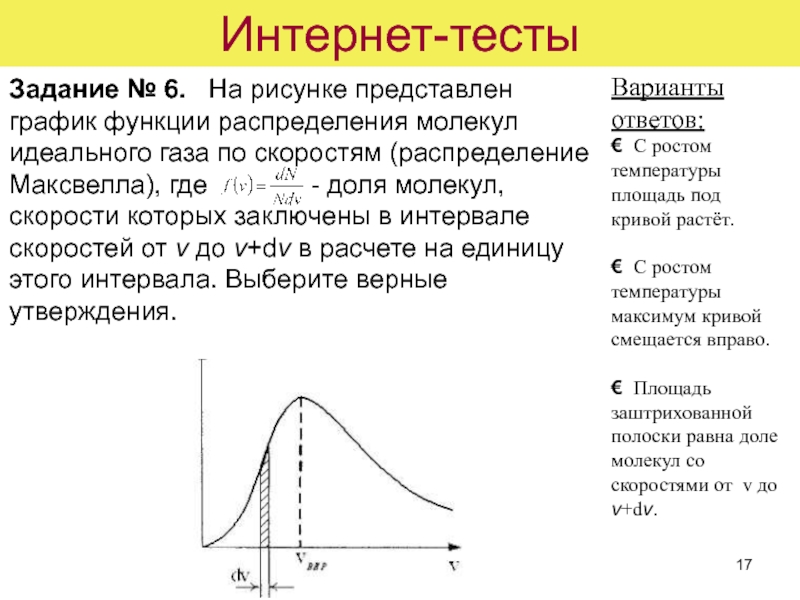
Задание № 6. На рисунке представлен график функции распределения
молекул идеального газа по скоростям (распределение Максвелла), где
- доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала. Выберите верные утверждения.Варианты ответов:
С ростом температуры площадь под кривой растёт.
С ростом температуры максимум кривой смещается вправо.
Площадь заштрихованной полоски равна доле молекул со скоростями от v до v+dv.