Слайд 12.12. Корреляция.
Понятие корреляционной связи
Слайд 21
В статистике различают функциональную и стохастическую связи.
Функциональной называют такую связь, при которой имеется однозначное соответствие между
факторными и результативными признаками.
При стохастической связи причинная зависимость между факторными и результативными признаками проявляется не в каждом отдельном случае, а лишь при большом числе наблюдений. В каждом конкретном случае при изменении одной переменной вторая может принимать в определенных пределах любые значения с некоторой вероятностью.
Слайд 32
Корреляционной связью называют такой частный случай стохастической связи,
при которой различным значениям факторного признака соответствуют различные средние значения
результативного признака.
Слайд 43
По направлению выделяют связь прямую и обратную.
При прямой связи увеличение или уменьшение факторного признака
приводит к увеличению или уменьшению результативного признака (или его среднего значения).
При обратной связи увеличение факторного признака приводит к уменьшению результативного.
Слайд 54
По аналитическому выражению связи могут быть линейными и
нелинейными.
Если статистическая связь между явлениями может
быть приближенно выражена прямой линией, то связь называется линейной, если же она выражается уравнением какой-либо другой линии (параболы, гиперболы и т. д.), то связь называют нелинейной.
Слайд 65
Принято различать:
а) парную корреляцию - связь между результативным
и факторным признаками;
б) частную корреляцию - связь между результативным признаком
и одним факторным признаком при фиксированном значении всех других факторных признаков;
в) множественную корреляцию - связь между результативным признаком и двумя и более факторными признаками.
Слайд 76
Задачей эконометрического анализа является определение аналитического
выражения уравнения связи, которое может зависеть от одного факторного признака
(однофакторная регрессия) или от двух и более факторных признаков (множественная регрессия).
Слайд 87
В некоторых случаях можно ограничиться лишь качественными результатами
о наличии корреляции между признаками и ее направлении.
Для получения такой информации используются метод построения поля корреляции т.е. точечной диаграммы. Причем по оси Х откладывается значение факторного признака а по оси Y результативного.
Слайд 98
Вернемся к примеру
рассмотренному во введении. На основании данных о годовом располагаемом доходе
и годовых расходах на личное потребление в 1999 г. для 20 семей (в условных единицах), требуется выяснить существует ли взаимосвязь между располагаемым доходом и расходами на личное потребление.
Слайд 109
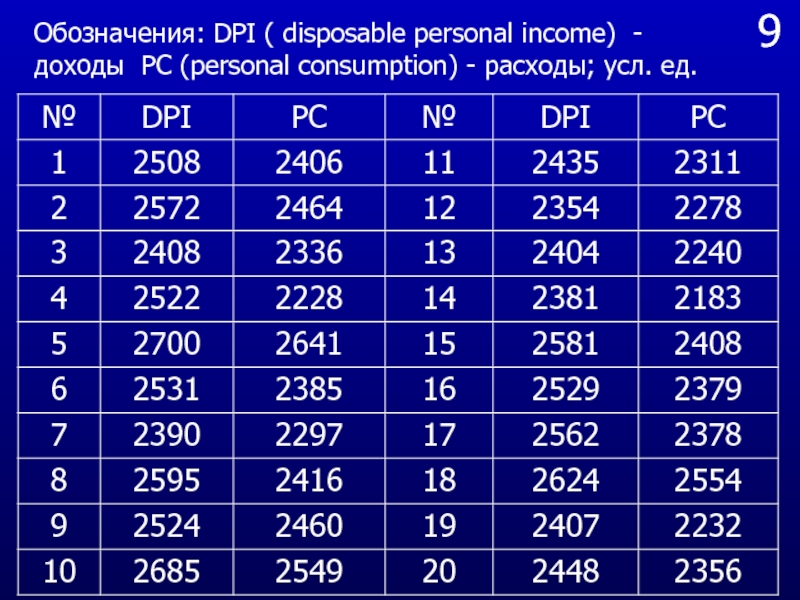
Обозначения: DPI ( disposable personal income) - доходы PC (personal
consumption) - расходы; усл. ед.
Слайд 1110
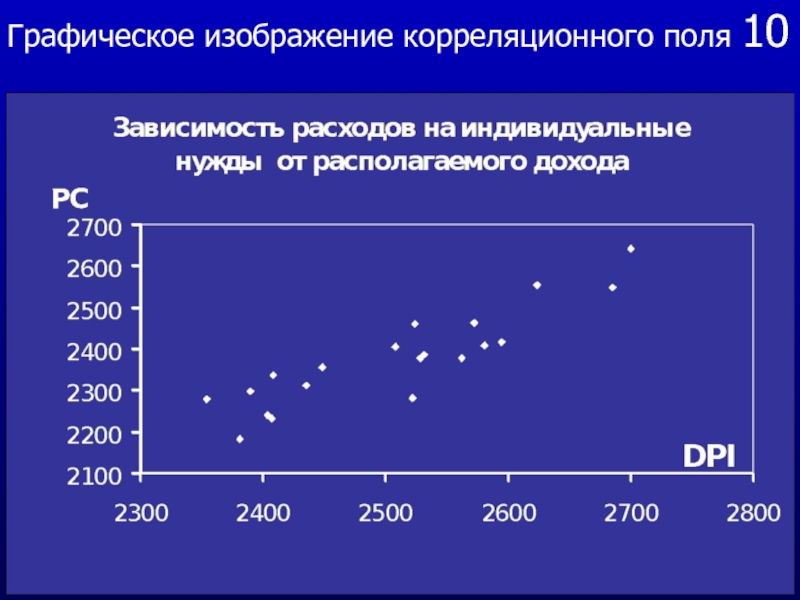
Графическое изображение корреляционного поля
Слайд 1211
Расположение точек на графике отражает общую
тенденцию вариации факторного и результативного признаков.
Теперь хорошо
видно, что корреляция (взаимосвязь) признаков существует, но хотелось бы получить количественную оценку тесноты этой связи.
Для количественной оценки тесноты корреляции в случае, когда связь линейна вычисляют коэффициент корреляции r.
Слайд 1312
Определим линейный коэффициент корреляции как среднее значение произведения нормированных отклонений
результативного и факторного признаков от их средних значений:
Слайд 1413
Линейный коэффициент корреляции может принимать значения
в пределах от -1 до +1 .
При наличии функциональной связи коэффициент корреляции равен по модулю единице, а при отсутствии связи - нулю.
Слайд 1514
Эмпирическая схема определения тесноты связи
Слайд 1615
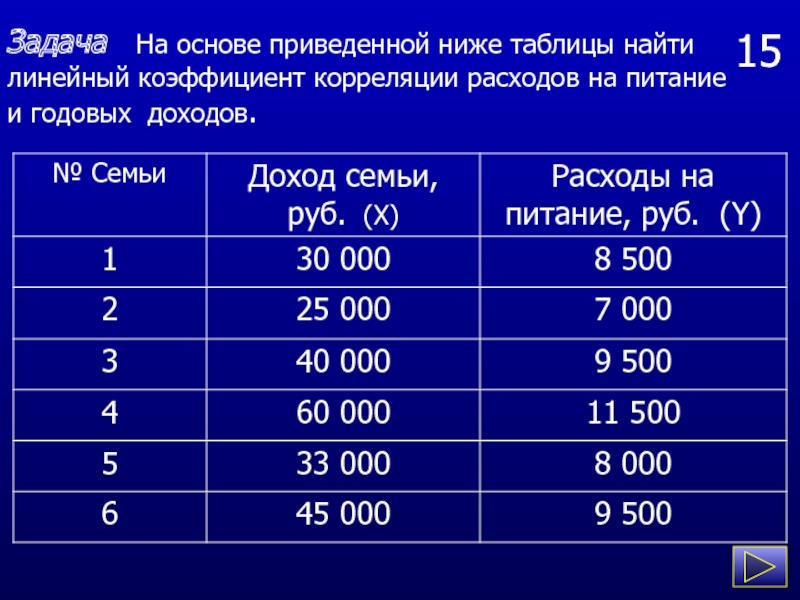
Задача На основе приведенной ниже таблицы найти линейный коэффициент
корреляции расходов на питание и годовых доходов.
Слайд 1716
Найдем среднее значение и дисперсию признаков X и
Y, используя стандартные функции Excel Срзнач () и Диспр ().
В результате получаем следующие значения
Коэффициент корреляции можно найти и с помощью стандартной функции Коррел(). Как и следовало ожидать, корреляция между доходами и расходами на питание является сильной.
Слайд 182.13. Статистическая
проверка гипотез
Слайд 191
Под статистической гипотезой понимают различного рода предположения о характере
или параметрах распределения случайной величины , которые можно проверить, опираясь
на результаты выборочного наблюдения.
Статистическая проверка гипотез носит вероятностный характер и поэтому всегда существует риск совершить ошибку. Однако с помощью статистической теории можно оценить вероятность принятия ложного решения. Если эта вероятность мала, то решение можно считать статистически обоснованным.
Слайд 202
При проверке гипотез ошибки могут быть
двоякого рода:
а) ошибка первого рода – проверяемая гипотеза
(ее обычно называют нулевой гипотезой) является в действительности верной, но в результате статистической проверки принимается решение об отказе от нее (нулевая гипотеза отвергается).
б) Ошибка второго рода — нулевая гипотеза в действительности является ошибочной, но в результате статистической проверки она принимается.
Слайд 213
Статистическая проверка гипотез осуществляется на основании
некоторых критериев.
Для построения такого критерия необходимо:
а) сформулировать нулевую гипотезу (ее обычно обозначают символом Н0);
б) сформулировать альтернативную гипотезу (ее обычно обозначают символом Н1);
в) выбрать уровень значимости , контролирующей допустимую ошибку первого рода;
г) определить область допустимых значений и критическую область для изучаемого показателя;
д) принять то или иное решение на основании сравнения наблюдаемого и критического значения показателя.
Слайд 224
Уровнем значимости будем называть такое
малое значение вероятности попадания критерия в критическую область при условии
справедливости гипотезы, что появление этого события можно расценивать как существенное расхождение выдвинутой гипотезы с результатом выборочного наблюдения. Обычно уровень значимости принимают равным 0,05 или 0,01.
К критической области относят те значения изучаемого показателя, которые при условии верности гипотезы являются весьма мало вероятными
Слайд 235
Вероятность совершить ошибку первого
рода т. е. отвергнуть гипотезу Н0 когда она верна, называется
уровнем значимости критерия.
Мощностью критерия называется вероятность 1 – не допустить ошибку 2-го рода т.е.отвергнуть гипотезу Н0 , когда она неверна.
Если принять юридическую терминологию, то - это вероятность осудить невиновного, а - вероятность оправдать виновного.
Слайд 246
Величина ошибки первого и второго рода однозначно
определяется выбором критической области. Совершенно естественно их хочется сделать
одновременно по возможности малыми. Однако это требование является противоречивым. Уменьшение одной величины приводит к росту другой. Лишь увеличение объема выборки позволяет уменьшать обе величины одновременно.
Важно отметить, что проверка статистической гипотезы не дает логического доказательства ее верности или неверности.
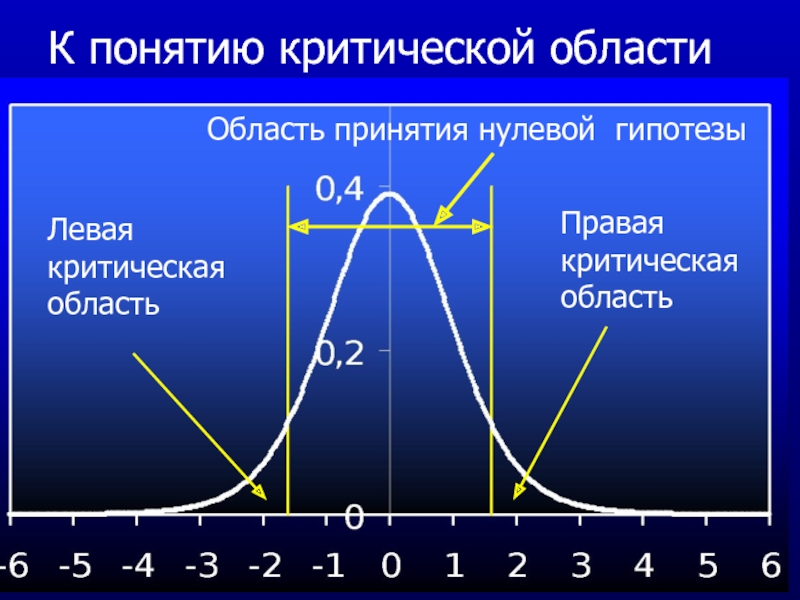
Слайд 25К понятию критической области
Правая критическая область
Левая критическая область
Область принятия нулевой
гипотезы
Слайд 262.14. Статистическая оценка значимости линейного коэффициента корреляции
Слайд 271
Для ответа на вопрос о значимости коэффициента корреляции
необходимо при заданном уровне значимости проверить нулевую гипотезу H0
(о равенстве нулю генерального коэффициента корреляции) при конкурирующей гипотезе H1 (об отличии от нуля генерального коэффициента корреляции).
Если нулевая гипотеза будет отвергнута, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля.
Слайд 282
Для проверки нулевой гипотезы рассмотрим величину
При справедливости нулевой гипотезы случайная величина t подчиняется
распределению Стьюдента с k = n-2 степенями свободы, где n – объем выборки; (предполагается, что в генеральной совокупности распределение является нормальным).
Слайд 293
Отсюда следует простое правило: для того, чтобы
при заданном уровне значимости проверить нулевую гипотезу о равенстве
нулю генерального коэффициента корреляции при конкурирующей гипотезе , следует вычислить эмпирическое значение критерия
Слайд 304
Затем по таблице критических точек распределения Стьюдента
при данном числе степеней свободы и уровне значимости найти значение
критической точки t кр . Если
то нулевую гипотезу следует отвергнуть и это значит, что выборочный коэффициент корреляции значим. В противном случае отличие от нуля выборочного коэффициента корреляции можно объяснить действием случайных причин.
Слайд 315
Применим изложенный выше подход к рассматриваемой задаче . Подставляя
численные значения
, получаем t эмп = 7,988. Зададимся уровнем значимости 0,01. По таблице критических точек распределения Стьюдента находим, что при числе степеней свободы K=4, уровне значимости равном 0,01 значение tкр =4,404 . Поэтому нулевая гипотеза должна быть отвергнута, и можно говорить, что в генеральной совокупности существует прямая связь между доходами семьи и затратами на питание.
Слайд 331
Рассмотрим теперь задачу об определении уравнения линии
регрессии. Теоретической линией регрессии называется такая линия, вокруг которой группируются
точки корреляционного поля и которая указывает основное направление связи. Чаще всего уравнение регрессионной линии определяется по методу наименьших квадратов.
Слайд 342
Обсудим применения этого метода для случая, когда предполагается линейная
связь между факторным и результативным признаками. Пусть имеется два набора
данных хi и yi, i=1,2…n Требуется найти уравнение прямой
для которой сумма квадратов отклонений (ошибок)
была бы минимальной.
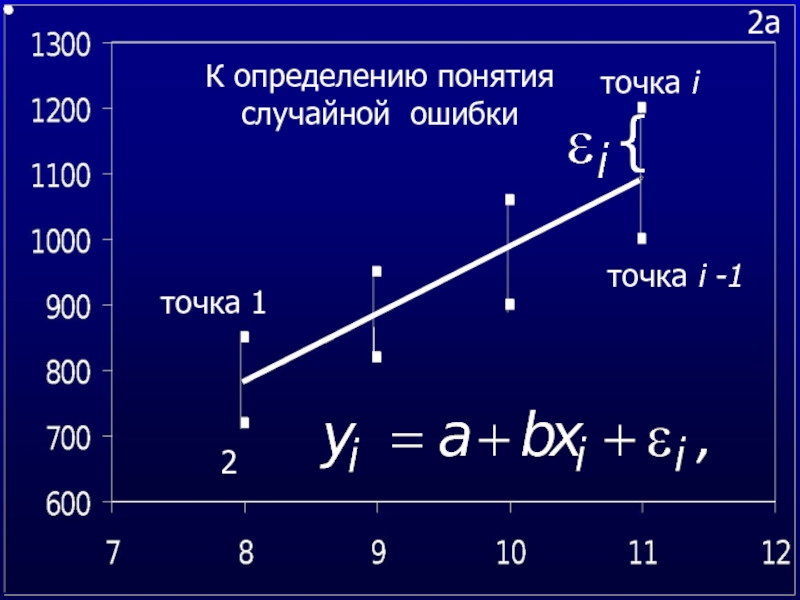
Слайд 352a
2a
К определению понятия случайной ошибки
точка 1
2
точка i
точка i -1
Слайд 363
Очевидно, что S является функцией двух переменных, и поэтому
условие минимума дает два уравнения:
После несложных преобразований получаем
систему нормальных уравнений способа наименьших квадратов для определения двух неизвестных параметров прямой a и b:
Слайд 374
Действительно. Подставим
в выражение для S и продифференцируем это выражение
по а:
Отсюда получаем первое уравнение:
Аналогично выводится и второе уравнение.
Слайд 384а
Таким образом, получаем следующую систему нормальных уравнений для определения коэффициентов
регрессии
Слайд 395
Решая систему двух уравнений относительно неизвестных коэффициентов a
и b, получаем расчетные формулы
Слайд 406
Параметр b называют коэффициентом регрессии. Коэффициент регрессии используют
для определения параметра эластичности
Между коэффициентом регрессии и линейным
параметром корреляции существует простое соотношение:
где
коэффициенты среднего квадратического отклонения факторного и результативного признаков.
Слайд 417
Воспользуемся данными табл. на слайде 16 и найдем параметры
линейной регрессионной модели для этой задачи. Коэффициент корреляции и другие
необходимые параметры мы вычисляли ранее см. слайд 17 : Напомним результат
В результате получаем параметры уравнения регрессии
Слайд 428
Следовательно уравнение регрессии будет иметь вид
Слайд 439
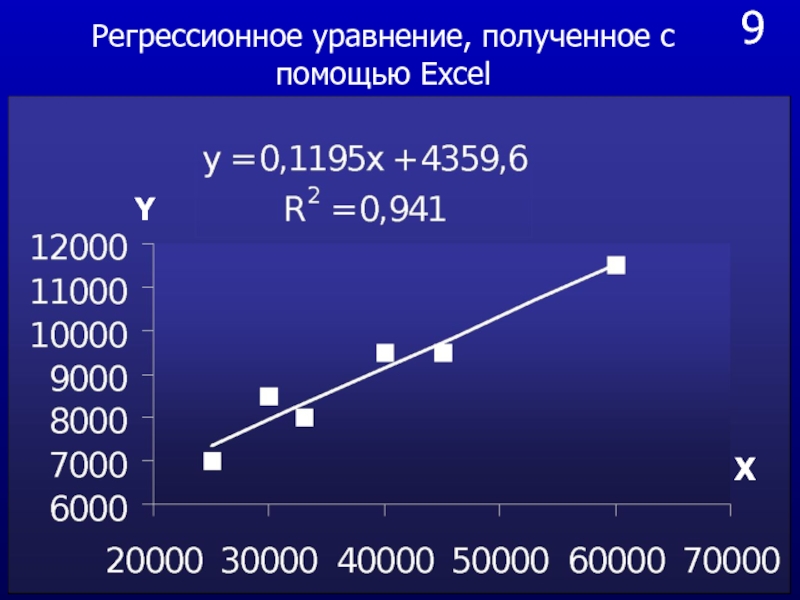
X
Y
Регрессионное уравнение, полученное с помощью Excel
Слайд 449
Хотя выше был рассмотрен лишь с случай линейной функции,
во многих случаях можно использовать эти же формулы для коэффициентов
регрессии, выполнив простую замену переменных. Пусть, например, изучаемая модель описывается степенной функцией
где С – некоторая константа. Чтобы привести задачу построения кривой регрессии к линейному случаю для этой модели, достаточно по осям координат откладывать не значения результативного и факторного признаков, а их логарифмы (процедура линеаризации).
Слайд 4510
Действительно, прологарифмировав уравнение степенной зависимости, имеем линейную зависимость для логарифмов
Аналогично
можно подобрать подходящую замену переменных и во многих других случаях.
Некоторые
примеры линеаризации будут рассмотрены в качестве примера на лекциях и практических занятиях.
Слайд 463. 1. Оценка значимости регрессионной модели.
Коэффициент детерминации
Слайд 471
В рассматриваемой линейной модели регрессии вариация зависимой
переменной y не может быть объяснена только действием фактора
х, поскольку действуют и другие неучтенные моделью причины вариации величины y.
Поэтому в общем случае уравнение регрессии будет иметь вид
где
случайный член, (необъясненный остаток) характеризующий отклонение эмпирических точек от функции регрессии.
Слайд 482
Отметим основные постулаты, которые должны выполняться для того, чтобы можно
было считать применение регрессионного анализа обоснованным.
1. В рассматриваемой регрессионной модели
случайными величинами являются а xi случайной величиной не является.
2. Математическое ожидание
3. Дисперсия возмущения или зависимой переменной yi постоянна и не зависит от номера точки i (условие гомоскедастичности или равноизменчивости возмущения)
Слайд 493
4. Возмущения являются
независимыми. Отсюда следует, что
5. Возмущение или
зависимая переменная уi распределены по нормальному закону. Последнее условие позволяет произвести оценку статистической значимости модели и коэффициентов регрессии.
Регрессионная модель удовлетворяющая этим пяти требованиям называется классической нормальной линейной регрессионной (КНЛР) моделью.
Слайд 504
Для КНЛР - модели доказано несколько важных математических теорем, которые
мы примем без доказательства.
Теорема Гаусса-Маркова
Если
регрессионная модель удовлетворяет условиям 1 - 4, то полученные оценки для коэффициентов a и b имеют наименьшую дисперсию среди всех линейных несмещенных оценок. Иначе говоря, эти оценки являются эффективными (наилучшими среди других возможных).
Слайд 515
Одной из задач регрессионного анализа является оценка
адекватности модели. Для проверки того, насколько хорошо кривая регрессии представляет
набор эмпирических данных, определяется коэффициент детерминации (пользователи электронных таблиц EXCEL знают ее как фактор детерминации R2).
Слайд 526
Оценка адекватности линейной модели регрессии на
основе вычисления фактора детерминации и оценка значимости уравнения регрессии с
помощью критерия Фишера основаны на использовании идей дисперсионного анализа. В своей сущности эти идеи достаточно просты и мы их изложим в применении к линейной модели регрессии
Слайд 537
Основная идея метода состоит
в том, чтобы разделить общую вариацию факторного признака на часть,
которая объясняется регрессионной моделью (действием изучаемого фактора), и часть не находящую объяснения в данной модели (объясняется действием неучтенных факторов):
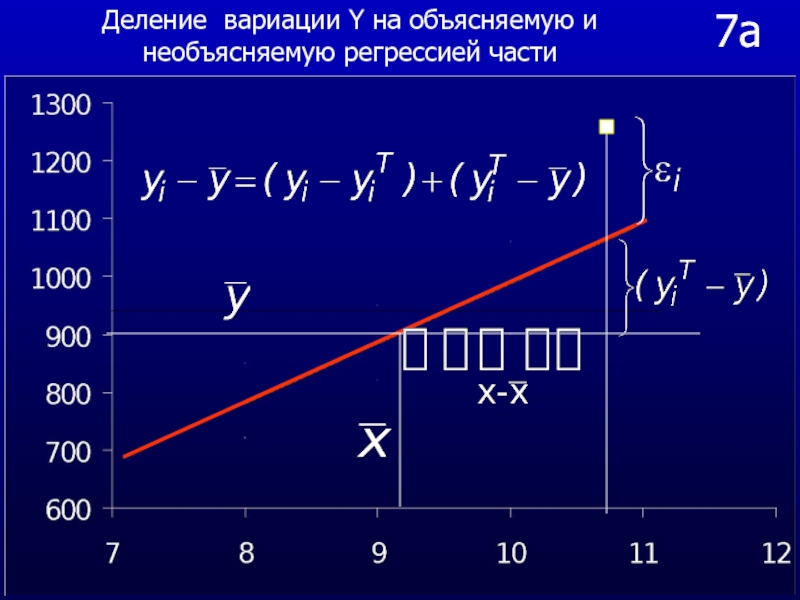
Слайд 547а
Деление вариации Y на объясняемую и необъясняемую регрессией части
Слайд 557б
При возведении в квадрат и последующем суммировании получаем
Преобразуем последнее слагаемое.
Первое произведение представим в виде
Этот результат прямо следует из рисунка
на предыдущем слайде.
Слайд 567в
Для преобразования второго сомножителя преобразуем сначала последнее выражение
И подставим этот
результат в рассматриваемый член. В результате получаем
Теперь подставим оба преобразованных
сомножителя в изучаемую сумму. В итоге получаем
Слайд 577г
Поскольку, как было показано ранее, коэффициент b может быть представлен
в виде
Слайд 588
Величина QR дает сумму квадратов отклонений, объясненной моделью
(Regression sum of squares). Будем использовать для ее обозначения аббревиатуру
RSS.
QE – характеризует влияние неучтенных факторов. Ее называется чаще всего суммой квадратов ошибок (Error sum of squares). Для ее обозначения будем использовать абривеатуру ESS
Величину QT в левой части формулы будем называть полной суммой квадратов (Total sum of squares) и использовать для ее обозначения аббревиатуру TSS.
Слайд 598а
Очевидно, что если QR >> QE , то
уравнение регрессии статистически значимо и фактор х оказывает существенное влияние
на результат y.
Для получения количественной оценки, выдвинем нулевую гипотезу H0 утверждающую, что влияние фактора х является несущественным.
В условиях справедливости выдвинутой гипотезы оценка дисперсии в генеральной совокупности не должна зависеть от способа получения этой оценки.
Слайд 608б
Напомним, что для получения несмещенной оценки дисперсии, сумму квадратов отклонений
от средней следует делить не на число наблюдений, а на
число степеней свободы, т. е. число наблюдений за вычетом числа наложенных на эти наблюдения связей.
Составим схему дисперсионного анализа, позволяющие получить несмещенные оценки дисперсии зависимой переменной.
Слайд 629
Рассмотрим две оценки дисперсии
где m число параметров в уравнении
регрессии, n – число наблюдений. Обе эти величины являются случайными
и распределены по закону хи-квадрат с m-1 и n-m числом степеней свободы. Отношение этих величин подчиняется статистике Фишера-Снедекора и обычно используется для оценки значимости регрессионной модели. Критерий Фишера)
Слайд 6310
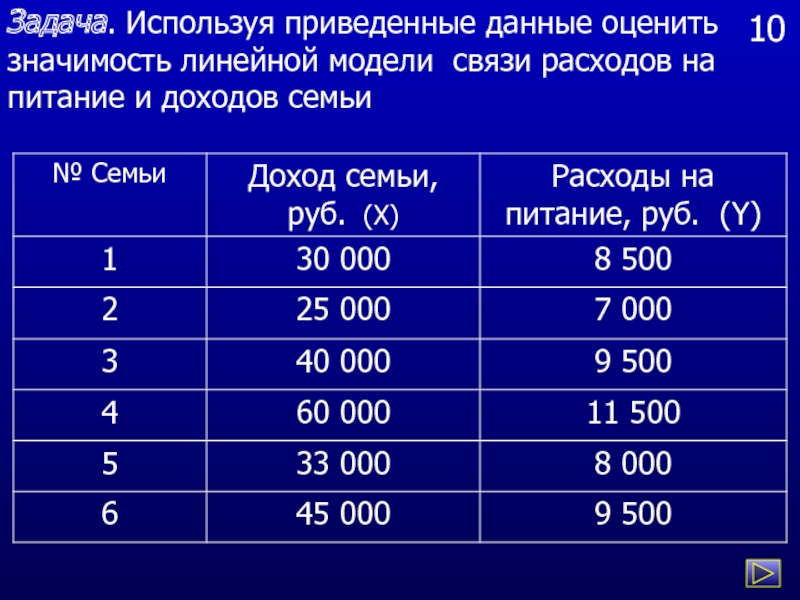
Задача. Используя приведенные данные оценить значимость линейной модели связи расходов
на питание и доходов семьи
Слайд 6411
Линейное регрессионное уравнение было получено ранее и имеет
вид
Используя электронные таблицы Excel, находим суммы квадратов отклонений
. Найдем расчетное значение критерия Фишера F, учитывая, что в нашем случае m = 2, n = 6
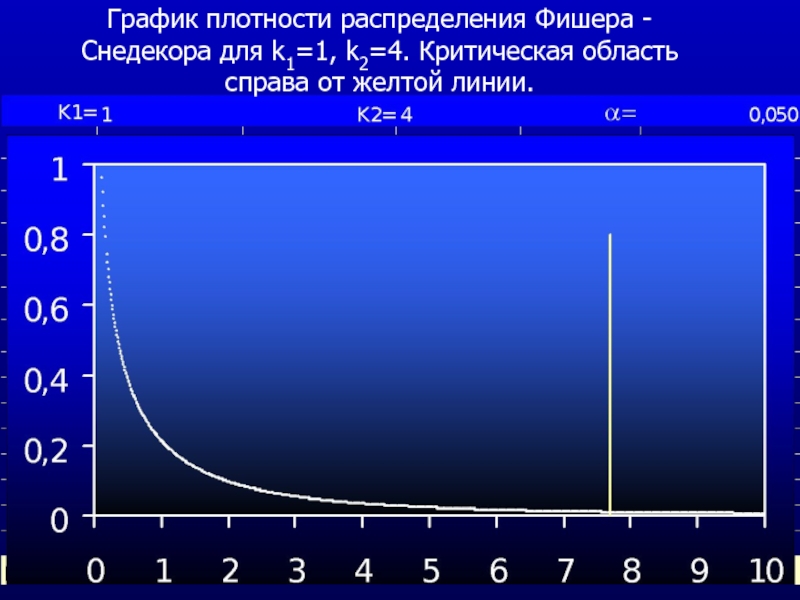
Слайд 6512
Величина F подчиняется распределению Фишера –Снедекора для
K1=1, K2=4.
Используя функцию Excel FРАСПОБР(0,05;1;4) Получаем критическое
значение статистики Фишера - Снедекора для уровня значимости 0,05 Fкрит = 7,72. Поскольку эмпирическое значение значительно превышает критическое, то гипотезу об отсутствии связи между признаками Y и Х следует отбросить и признать, что регрессионное уравнение является значимым.
Слайд 66График плотности распределения Фишера -Снедекора для k1=1, k2=4. Критическая область
справа от желтой линии.
Слайд 6713а
Для проверки значимости линейного уравнения регрессии можно
использовать и функцию ЛИНЕЙН ( ) электронных таблиц Excel.
Кроме значения критерия Фишера, эта функция возвращает и ряд других параметров регрессионной модели, важных для ее правильной статистической оценки. Применение функции ЛИНЕЙН ( ) для оценки значимости линейной модели рассмотрим на примере.
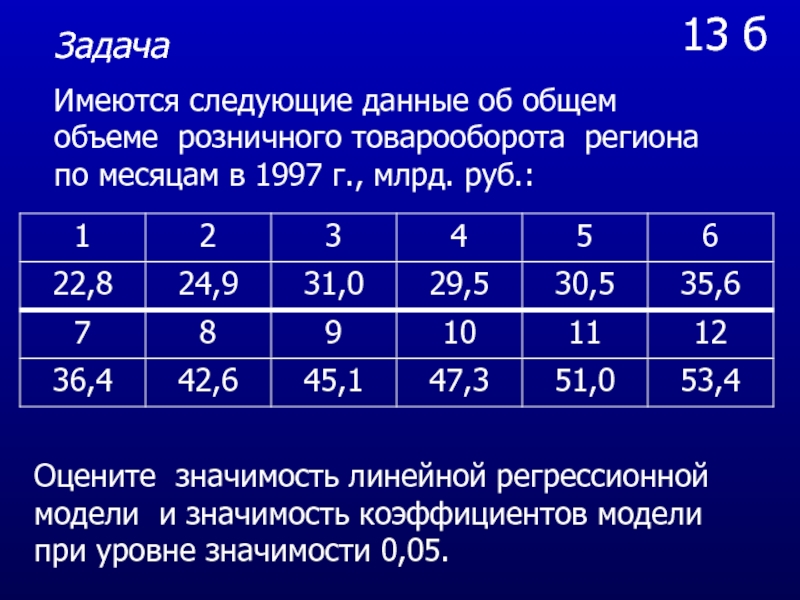
Слайд 6813 б
Задача
Имеются следующие данные об общем объеме розничного товарооборота
региона по месяцам в 1997 г., млрд. руб.:
Оцените значимость линейной
регрессионной модели и значимость коэффициентов модели при уровне значимости 0,05.
Слайд 6914
Sy
F
n-2
QR
Q E
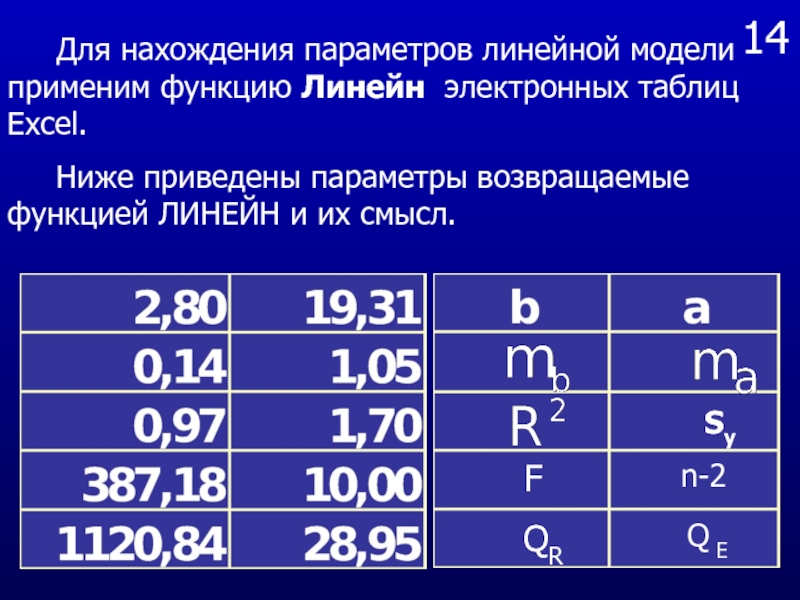
Для нахождения параметров линейной модели применим
функцию Линейн электронных таблиц Excel.
Ниже приведены параметры
возвращаемые функцией ЛИНЕЙН и их смысл.
Слайд 7015
Для оценки значимости регрессионной модели найдем критическую точку распределения
Фишера при уровне значимости 0,05 и числе степеней свободы k1=1
и k2=10, используя функцию Excel FРАСПОБР(0,05;1;10), которая возвращает значение 4,96. Поскольку эмпирическое значение коэффициента Фишера в рассматриваемой задаче равно 387,18, и превышает во много раз критическое значение, то необходимо признать, что рассматриваемая связь значима.
Уравнение регрессии имеет вид
Слайд 7116
Как уже указывалось, одной из наиболее эффективных оценок
адекватности регрессионных моделей, мерой качества уравнения регрессии является фактор детерминации
R2 . Для расчета этого коэффициента используются величины QR QE и QT :
Коэффициент детерминации изменяется в пределах от 0 до 1. Чем ближе коэффициент к единице, тем выше качество регрессионной модели.
В случае парной регрессии легко показать, что коэффициент детерминации равен квадрату коэффициента корреляции.
Слайд 7217
Действительно, вспоминая уравнение для определения коэффициента а и регрессионное уравнение
Подставляя
последний результат в определение коэффициента детерминации, получаем:
Слайд 7419
Следует заметить, что оценка качества регрессионного уравнения с помощью
критерия Фишера или коэффициента детерминации возможно только в том случае,
когда коэффициент а уравнения регрессии не равен нулю, поскольку только в этом случае возможно представление
Которое использовалось для доказательства возможности разбиения
Слайд 753. 2. Проверка значимости коэффициентов регрессии
Интервальная оценка для коэффициентов регрессии
и индивидуальных значений зависимой переменной.
Слайд 761
В линейной регрессии обычно оценивается значимость не только уравнения в
целом, но и отдельных его параметров Для оценки статистической значимости
коэффициентов регрессии используются случайные величины
mb и ma - стандартные ошибки коэффициентов регрессии. В качестве нулевой гипотезы выдвинем предположение, что
Слайд 772
В условиях справедливости выдвинутой гипотезы случайные величины
tb и ta подчиняются распределению Стьюдента. Поэтому для проверки
гипотезы нужно вычислить эмпирические значения tb и ta
и затем сравнить их с критическим значением статистики Стьюдента tкрит при заданном уровне значимости и числе степеней свободы n-2.
Слайд 783
Для нахождения mb найдем дисперсию коэффициента b. Для этого используем
запись коэффициента b в виде
Поскольку переменные Х не являются
случайными, то
Слайд 794
Оценим дисперсию используя формулу остаточной дисперсии. В условиях справедливости
выдвигаемой гипотезы (равенства нулю коэффициента b) такая оценка является справедливой.
Слайд 805
В итоге получаем среднеквадратическое отклонение (ошибку) для коэффициента b
в виде
Поэтому, если
то коэффициент b значим.
Слайд 816
интервальная оценка коэффициента при заданном уровне значимости (tкрит) определяется
стандартными формулами
Статистическая оценка значимости коэффициента а производится аналогично и мы
приведем формулы без дополнительных комментариев.
Слайд 826а
После такого преобразования коэффициента а, можно вычислить его дисперсию. Введем
обозначение
Найдем дисперсию коэффициента a.
Слайд 836б
Учитывая, что дисперсия суммы равна сумме
дисперсий, а также то, что величины xi не являются
случайными. получаем
поскольку сумма
после элементарных преобразований получаем
Слайд 847
Оценка значимости и расчет доверительного интервала
при заданном уровне значимости, определяется точно также как и для
коэффициента b.
Вспоминая выражение для дисперсии находим следующую оценку для средеквадратического отклонения коэффициента а
Слайд 858
Используя электронные таблицы Excel можно избежать утомительных вычислений, поскольку
функция ЛИНЕЙН ( ) возвращает и стандартные ошибки отклонений mb
ma.
Еще более полную информацию о параметрах регрессионной модели можно получить используя функцию РЕГРЕССИЯ из Пакета анализа.
Использование этого пакета будет продемонстрировано на практических занятиях.
Слайд 869
Построим доверительный интервал для функции регрессии
т. е. интервал значений переменной yТ, который при заданной доверительной
вероятности g = 1-a накроет неизвестное значение M(yT) при заданном значении аргумента х. Для этой цели точно также как и ранее, рассмотрим случайную величину
которая имеет распределение Стьюдента с k=n-2 степенями свободы.
Слайд 8710
Найдем среднеквадратическое отклонение для предсказываемых моделью значений yT
Дисперсия среднего значения
факторной переменной оценивается по известной формуле
где
генеральная дисперсия.
Слайд 8811
Дисперсия коэффициента b вычислялась ранее и равна
учитывая два последних
результата, получаем
Слайд 8912
В качестве оценки для дисперсии результативного признака снова возьмем
величину необъясненной дисперсии
В результате получаем выражение для ошибки
Слайд 9013
Поскольку случайная величина
подчиняется распределению Стьюдента с числом степеней свободы k=n-2,
то доверительный интервал для математического ожидания результативной переменной может быть
записан в виде
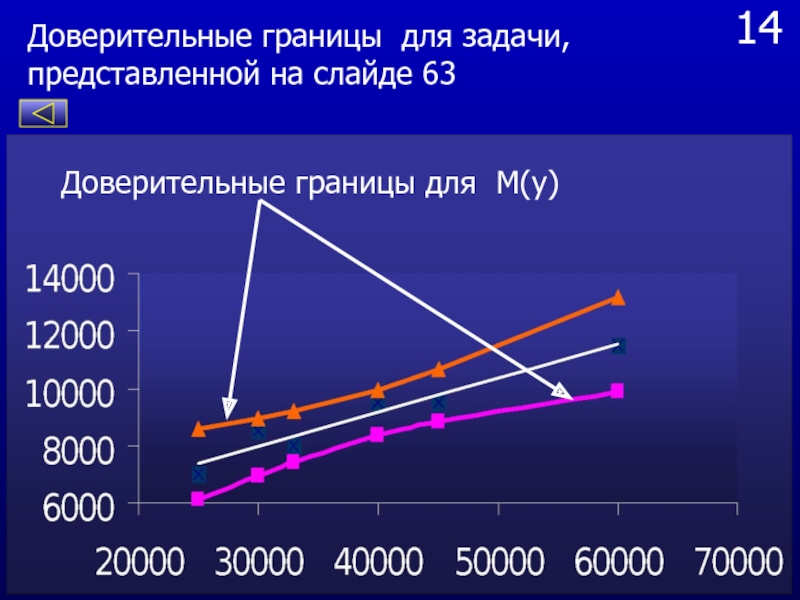
Слайд 9114
Доверительные границы для M(y)
Доверительные границы для задачи, представленной на слайде