2. КВАНТОВАЯ ПРИРОДА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 2.1. Элементарное введение До сих

имели дела с классическим ЭМ полем, которое описывается непрерывными функциями

времени и координат и подчиняется уравнениям Максвелла. Вместе с тем ясно, что любое поле имеет квантовую природу, в том числе и электромагнитное. В этом смысле фундаментальное ЭМ поле должно по своей природе быть квантовым.
Для перехода к квантовому описанию воспользуемся представлением вектора-потенциала поля. При этом предположим, что

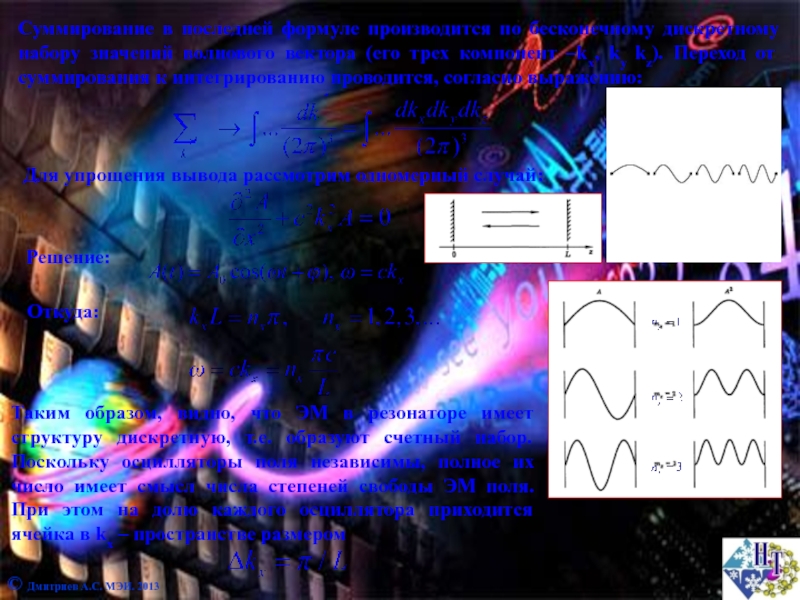
Пусть имеется объем, для которого формально V. Тогда поле в конечном объем можно разложить в ряды Фурье (по бегущим плоским волнам) в виде

© Дмитриев А.С. МЭИ. 2013

волнового вектора (его трех компонент –kx, ky kz). Переход от

суммирования к интегрированию проводится, согласно выражению:

Для упрощения вывода рассмотрим одномерный случай:

Решение:

Откуда:

Таким образом, видно, что ЭМ в резонаторе имеет структуру дискретную, т.е. образуют счетный набор. Поскольку осцилляторы поля независимы, полное их число имеет смысл числа степеней свободы ЭМ поля. При этом на долю каждого осциллятора приходится ячейка в kx – пространстве размером

© Дмитриев А.С. МЭИ. 2013

характеризуется тройкой натуральных чисел nj. Таким образом, все k-пространство разбивается

на кубики объемом

Вычислим теперь полное число степеней свободы ЭМ поля. Учитывая, что физически различным конфигурациям (осцилляторам) поля отвечают лишь положительные значения kj, а полный объем в k-пространстве есть

Тогда число степеней свободы поля есть отношение последнего объема к объему, занимаемому в k-пространстве одним осциллятором поля, т.е.

Учитывая, что на самом деле в одной волне есть два поля (компонента электрического и компонента магнитного, имеем окончательно число степеней свободы поля

© Дмитриев А.С. МЭИ. 2013

что удобно произвести замену вида (эти переменные вещественны)
Тогда
Полная энергия поля

тогда есть

В квантовой теории ей отвечает оператор энергии, выраженный через выписанные выше величины

Таким образом, общая энергия ЭМ поля представлена через переменные и операторы отдельных (независимых!) осцилляторов, для которых имеет место соотношений для уровней энергии

где - нумерует поляризацию

© Дмитриев А.С. МЭИ. 2013

, тогда энергия и импульс электромагнитного поля есть

Отсюда можно ввести понятие о квантах электромагнитного поля или фотонах. Это впервые сделано А. Эйнщтейном в 1905г. Согласно этой концепции, ЭМ поля можно рассматривать как совокупность частиц (квазичастиц), каждая из которых имеет энергию и импульс

Тогда величины представляют собой так называемые числа заполнения – число фотонов с данными импульсами и поляризацией . Представление в квантовой теории ЭМ поля через фотоны и числа заполнения полностью заменяет классическое его описание через напряженности поля или потенциалы. Заметим также, что ЭМ поле становится чисто классическим, когда велики числа заполнения . Отсюда также понятно, что фотоны должны подчиняться статистике Бозе-Эйнштейна, которая допускает любое число частиц в данном состоянии (в отличие от статистики Ферми-Дирака).

- рост чисел заполнения при переходе к классическому ЭМ полю

© Дмитриев А.С. МЭИ. 2013