Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
20.2. ТЕОРЕМА ГАУССА-ОСТРОГРАДСКОГО Эта формула связывает интеграл по объему V
Содержание
- 1. 20.2. ТЕОРЕМА ГАУССА-ОСТРОГРАДСКОГО Эта формула связывает интеграл по объему V
- 2. Пусть V – некоторая область в пространстве,
- 3. формулаГаусса-ОстроградскогоГде α, β, γ – углы, образованные внешней нормалью и осями x,y,z.
- 4. ДОКАЗАТЕЛЬСТВО:Рассмотрим область V, ограниченную поверхностью S. Пусть
- 5. Слайд 5
- 6. D – проекция областей S1 и S2
- 7. Верхняя и нижняя стороны являются внешними сторонами поверхности S, поэтому1
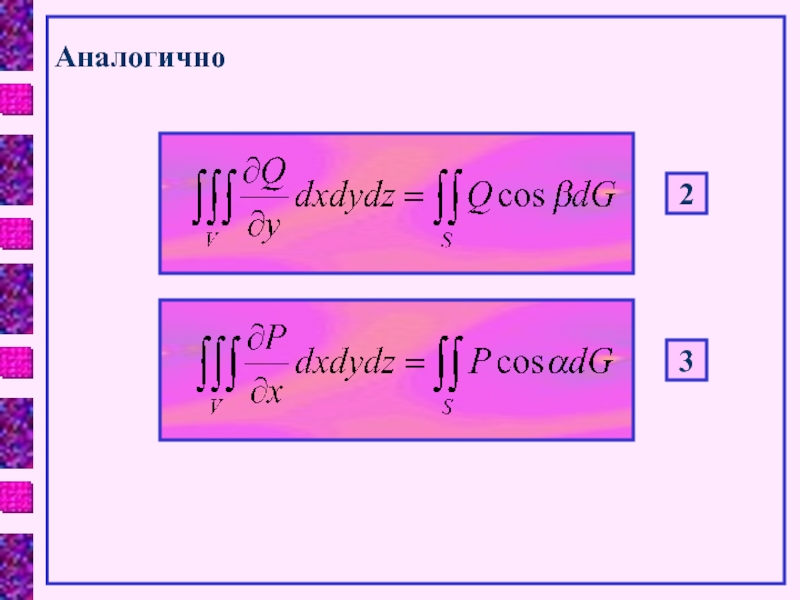
- 8. Аналогично23
- 9. Складываем почленно (1), (2), (3):
- 10. Скачать презентанцию
Пусть V – некоторая область в пространстве, S – граница этой области.Если функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными во всех точках области V, то справедлива формула:ТЕОРЕМА.
Слайды и текст этой презентации
Слайд 120.2. ТЕОРЕМА
ГАУССА-ОСТРОГРАДСКОГО
Эта формула связывает интеграл по
объему V с
интегралом по
Слайд 2Пусть V – некоторая область в
пространстве, S – граница
этой области.
Если функции P(x,y,z), Q(x,y,z), R(x,y,z)
непрерывны вместе со своими
частными производными во всех точках
области V, то справедлива формула:
ТЕОРЕМА.