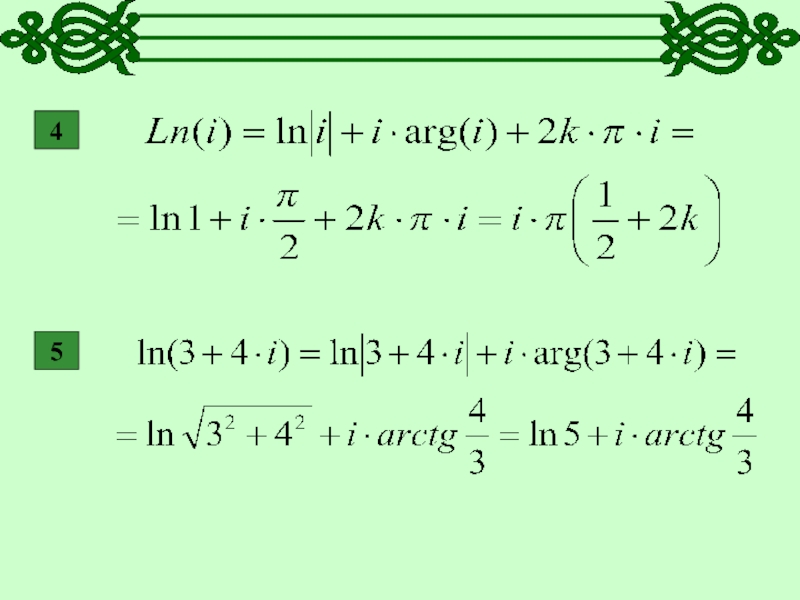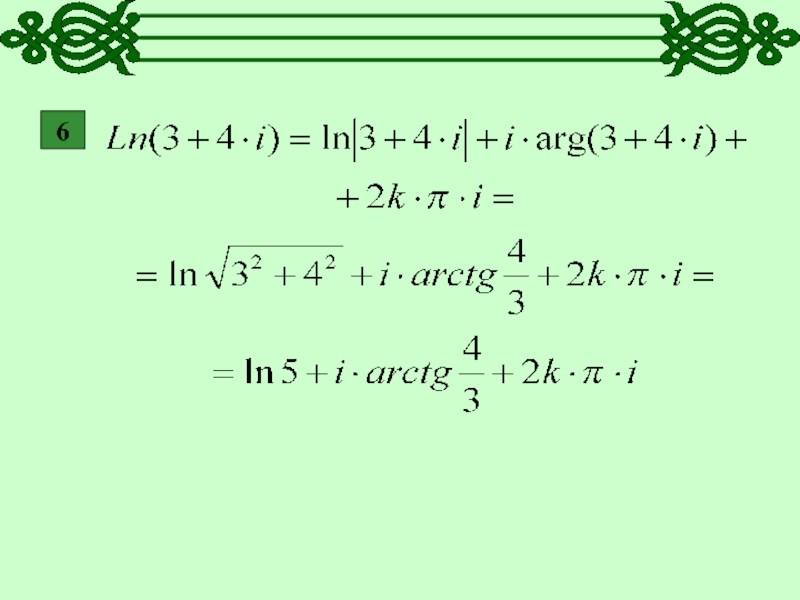Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
22.5. ЛОГАРИФМИЧЕСКАЯ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО
Содержание
- 1. 22.5. ЛОГАРИФМИЧЕСКАЯ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО
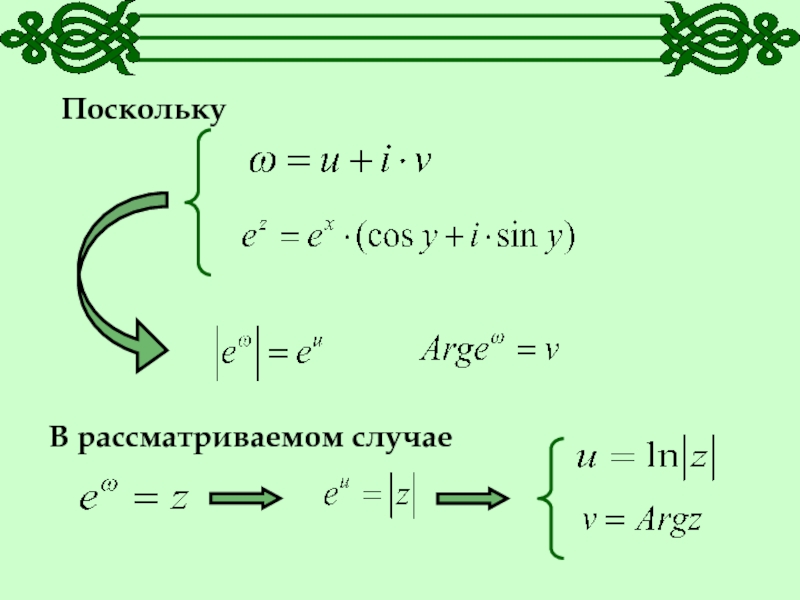
- 2. Поскольку В рассматриваемом случае
- 3. Где -число действительное и положительное.-известный из курса математики логарифм действительной величины.
- 4. Ввиду многозначности аргумента логарифм является многозначной функцией,
- 5. В полученной формуле главное значение логарифма будет
- 6. Будем обозначатьглавное значение логарифма
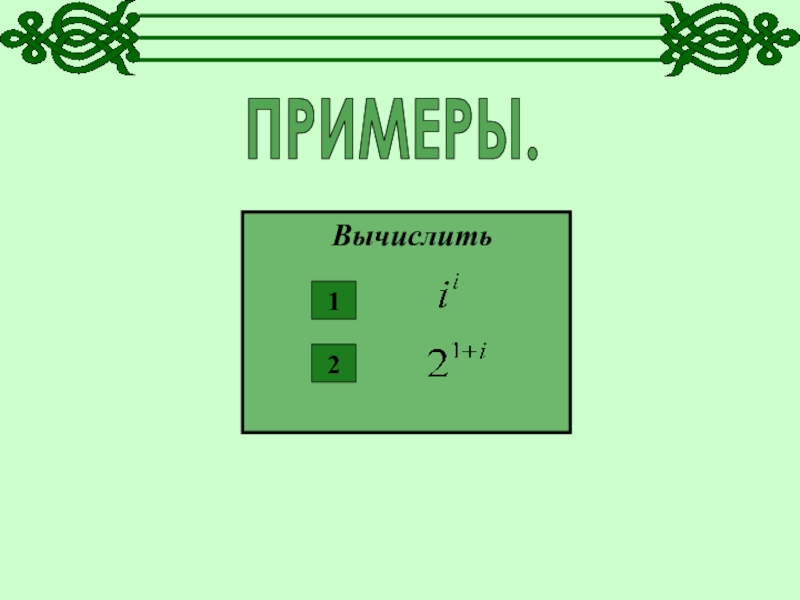
- 7. ПРИМЕРЫ.Вычислить 123456
- 8. РЕШЕНИЕ.123
- 9. 45
- 10. 6
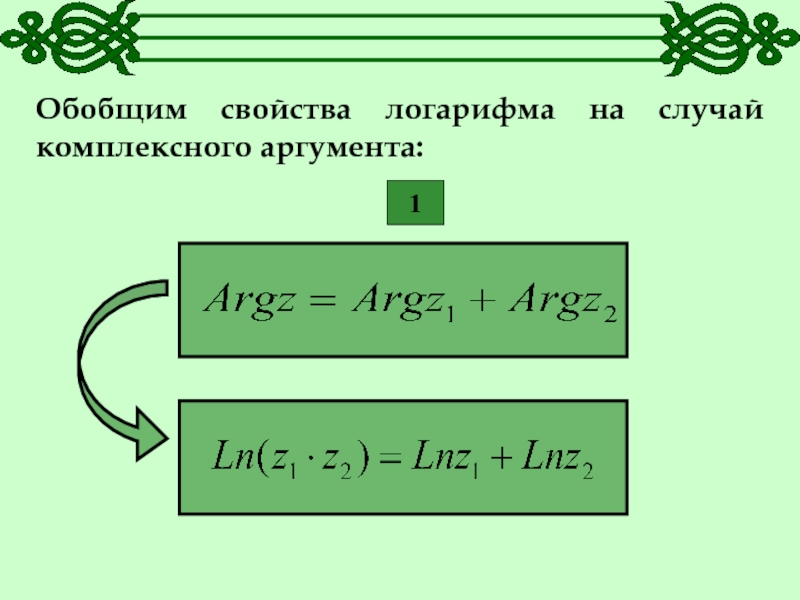
- 11. Обобщим свойства логарифма на случай комплексного аргумента:1
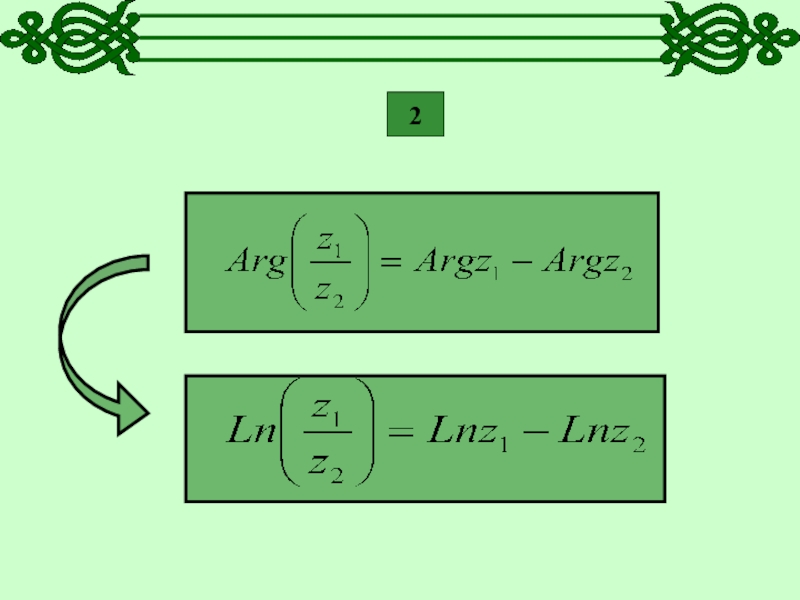
- 12. 2
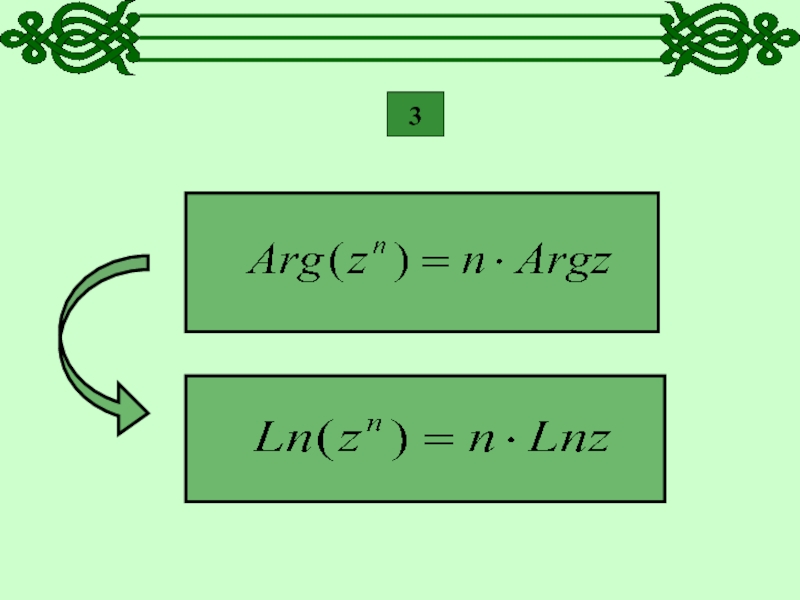
- 13. 3
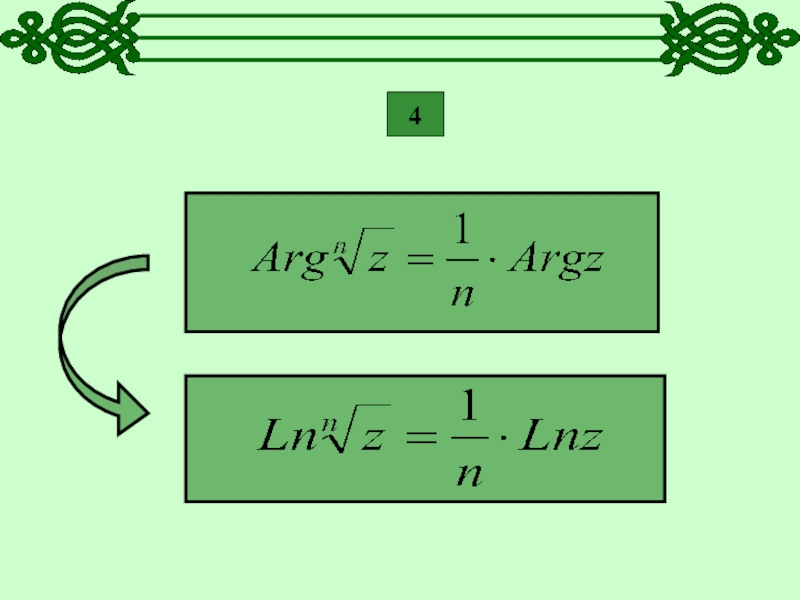
- 14. 4
- 15. По определению логарифмической функциидля любого комплексного числа
- 16. ПРИМЕРЫ.Вычислить 12
- 17. РЕШЕНИЕ.1Главное значение2
- 18. Определим обратные тригонометрические функции. Если то число w называется арксинусом числа z и обозначается Аналогично:
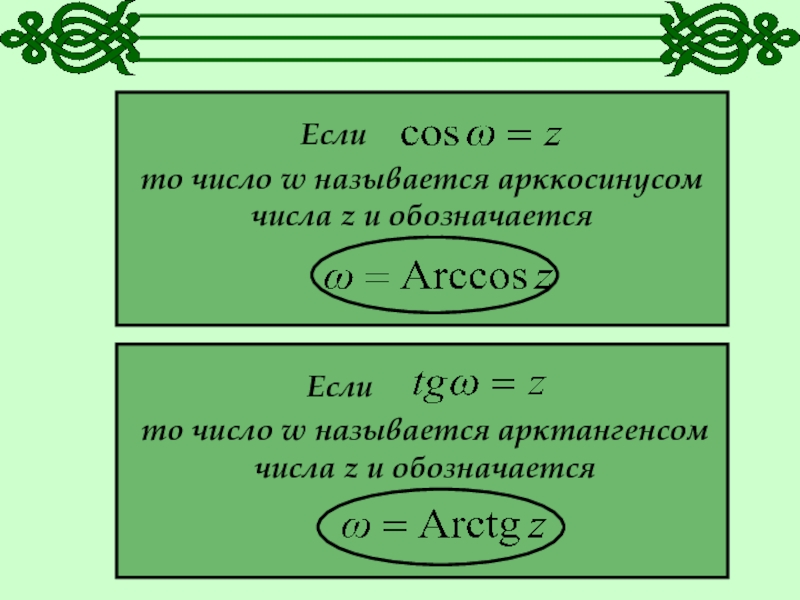
- 19. Если то число w называется арккосинусом числа
- 20. Если то число w называется арккотангенсом числа z и обозначается
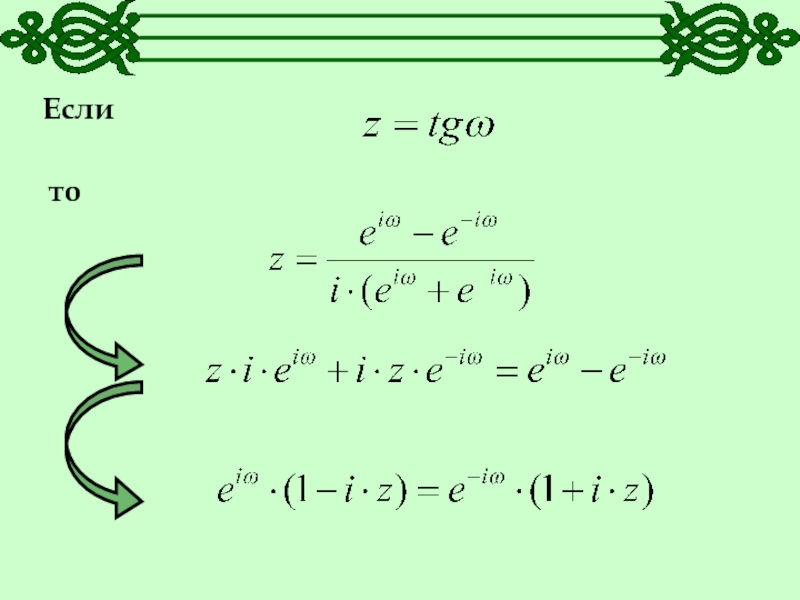
- 21. Если то Обозначим
- 22. Решаем это квадратное уравнение:
- 23. Т.к. логарифм многозначен, а корень – двухзначен,
- 24. Но поскольку то все значения логарифма числа,
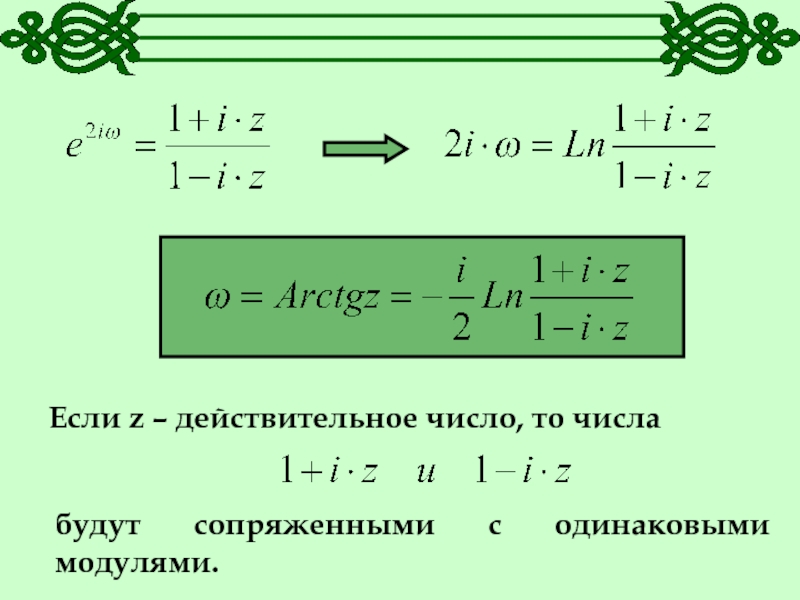
- 25. Если то
- 26. Если z – действительное число, то числабудут сопряженными с одинаковыми модулями.
- 27. Тогда все значения логарифма будут чисто мнимыми.
- 28. ПРИМЕРЫ.Вычислить 12
- 29. РЕШЕНИЕ.1
- 30. 2
- 31. Скачать презентанцию
Поскольку В рассматриваемом случае
Слайды и текст этой презентации
Слайд 122.5. ЛОГАРИФМИЧЕСКАЯ И
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Если
где
то число
w называется логарифмом числа z и обозначается
Слайд 3Где
-число действительное и положительное.
-известный из курса математики логарифм действительной
величины.
Слайд 4Ввиду многозначности аргумента логарифм является многозначной функцией, действительная часть которого
определяется
однозначно, а мнимая содержит неопределенное слагаемой, кратное 2П.
Главным значением логарифма
называется
то значение, котороесоответствует главному значению
аргумента числа z.
Слайд 5В полученной формуле главное значение логарифма будет при к=0.
Если z=x
– действительное число, то
Поэтому главное значение логарифма действительного положительного числа
является числом действительным и совпадает со значениемкоторое приводится в таблице логарифмов.
Слайд 15По определению логарифмической функции
для любого комплексного числа
Тогда
Поскольку логарифм
– многозначная функция, то функция
тоже будет многозначной.
Слайд 18Определим обратные тригонометрические функции.
Если
то число w называется арксинусом
числа z и обозначается
Аналогично:
Слайд 19Если
то число w называется арккосинусом числа z и обозначается
Если
то число w называется арктангенсом числа z и обозначается
Слайд 23Т.к. логарифм многозначен, а корень – двухзначен, то арксинус тоже
будет многозначной функцией.
Если z – действительное число,
то
-тоже действительная величина
и
Слайд 24Но поскольку
то все значения логарифма числа, модуль которого равен
1, являются чисто мнимыми, а так как в выражении для
арксинуса в правой части стоит –i, то в этом случае арксинус будет действительной величиной.В остальных случаях он будет мнимым.
Аналогично можно получить:
Слайд 27Тогда все значения логарифма будут чисто мнимыми. Поскольку стоит множитель
То
значения арктангенса будут действительными. В остальных случаях они будут мнимыми.
Аналогично
можно получить:
