Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
3.1.3 Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. 3.1.4
Содержание
- 1. 3.1.3 Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. 3.1.4
- 2. Слайд 2
- 3. Связь между параллельностью прямых и их перпендикулярностью
- 4. Признак перпендикулярности прямой и плоскости.Теорема. Если прямая
- 5. Замечания.Через любую точку пространства проходит плоскость, перпендикулярная
- 6. Наклонной, проведённой из данной точки к данной
- 7. Перпендикуляром, проведённым из данной точки к данной
- 8. Расстоянием от точки до плоскости называется длина перпендикуляра,
- 9. Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
- 10. Если AD>АВ, то DC>ВС.Если из данной точки
- 11. Теорема о трёх перпендикулярах: Если прямая, проведённая
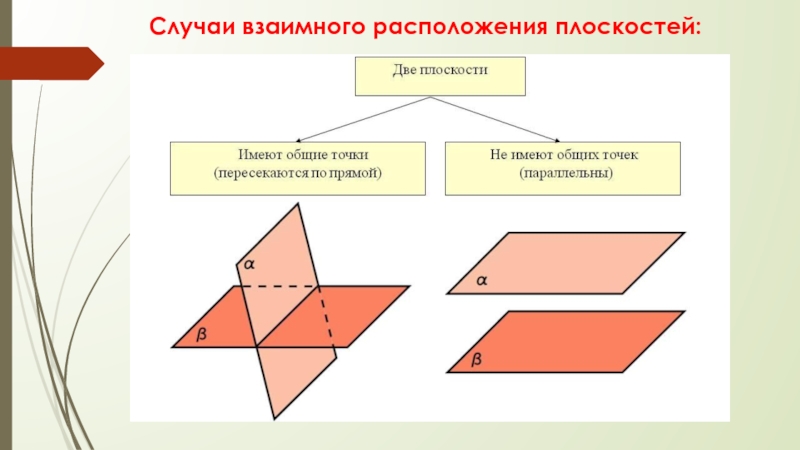
- 12. Случаи взаимного расположения плоскостей:
- 13. Свойства параллельных плоскостей:Если две параллельные плоскости пересечены
- 14. Теорема 1:Две плоскости параллельны, если одна из
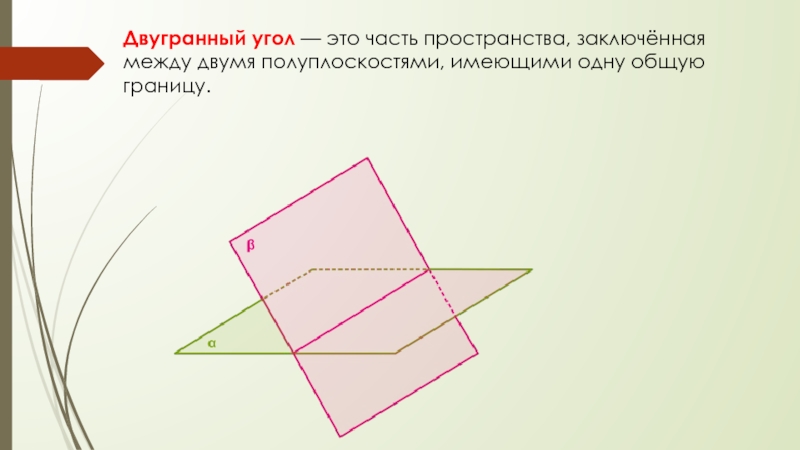
- 15. Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.
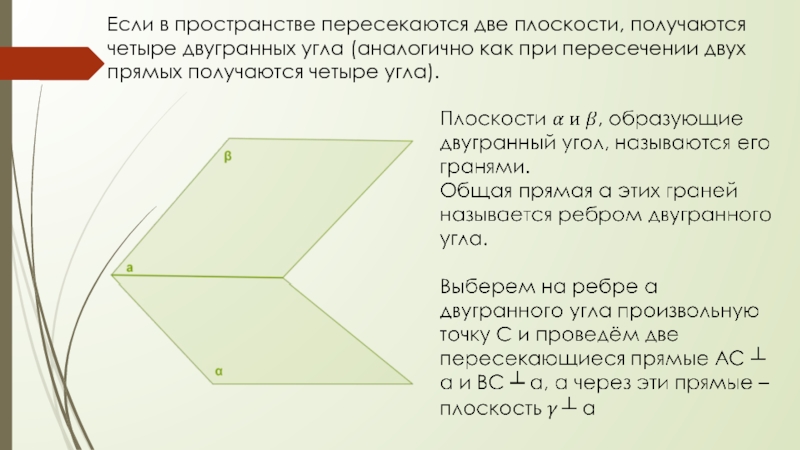
- 16. Если в пространстве пересекаются две плоскости, получаются
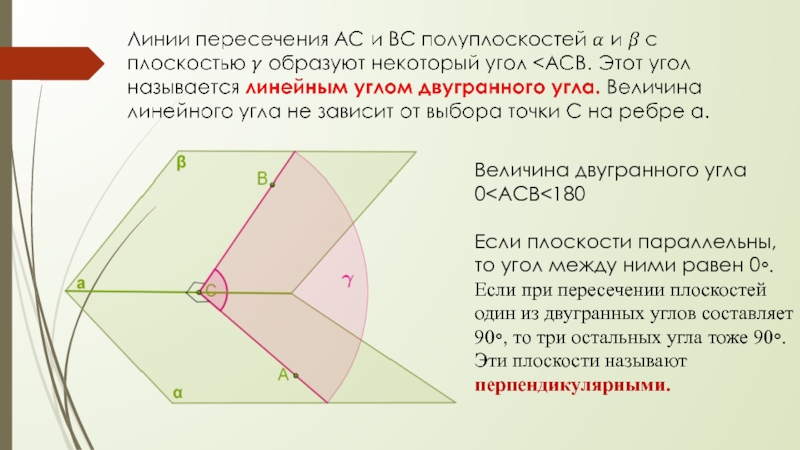
- 17. Величина двугранного угла 0
- 18. Теорема 4. Если одна из двух плоскостей
- 19. Слайд 19
- 20. Слайд 20
- 21. Скачать презентанцию
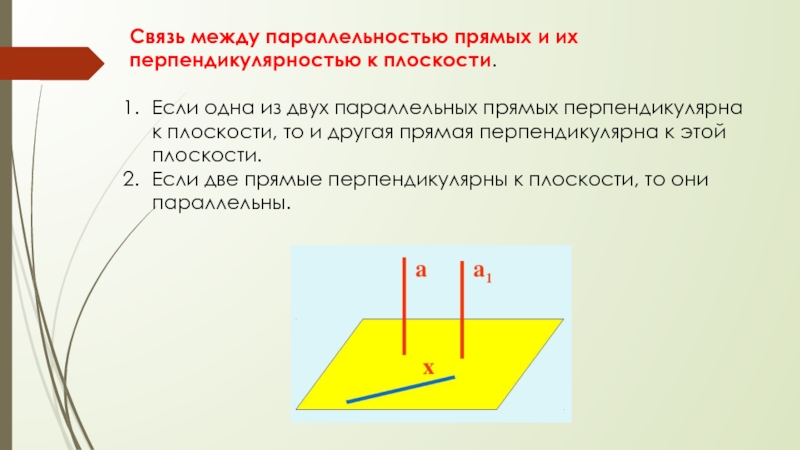
Связь между параллельностью прямых и их перпендикулярностью к плоскости.Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. Если две прямые перпендикулярны к плоскости,
Слайды и текст этой презентации
Слайд 13.1.3 Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная.
3.1.4 Угол между
прямой и плоскостью.
Перпендикулярность двух плоскостей.Слайд 3Связь между параллельностью прямых и их перпендикулярностью к плоскости.
Если одна
из двух параллельных прямых перпендикулярна к плоскости, то и другая
прямая перпендикулярна к этой плоскости.Если две прямые перпендикулярны к плоскости, то они параллельны.
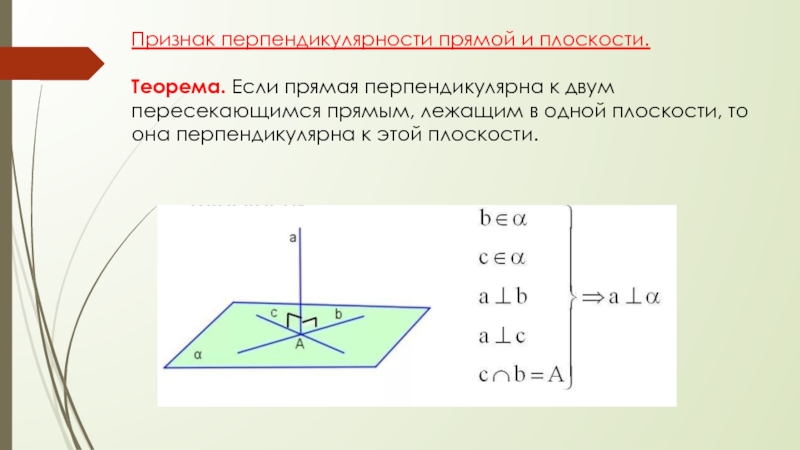
Слайд 4Признак перпендикулярности прямой и плоскости.
Теорема. Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к
этой плоскости.Слайд 5Замечания.
Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой,
и притом единственная.
Через любую точку пространства проходит прямая, перпендикулярная
к данной плоскости, и притом только одна. Если две плоскости перпендикулярны к прямой, то они параллельны.
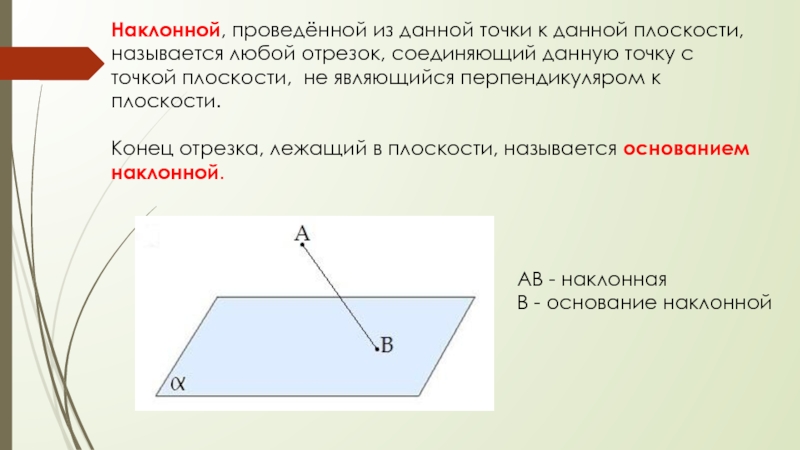
Слайд 6Наклонной, проведённой из данной точки к данной плоскости, называется любой
отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к
плоскости.Конец отрезка, лежащий в плоскости, называется основанием наклонной.
АВ - наклонная
В - основание наклонной
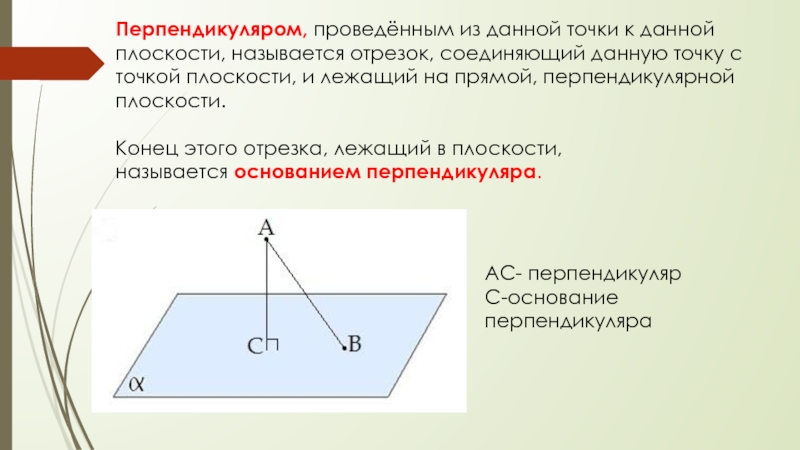
Слайд 7Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок,
соединяющий данную точку с точкой плоскости, и лежащий на прямой,
перпендикулярной плоскости.Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
АС- перпендикуляр
С-основание перпендикуляра
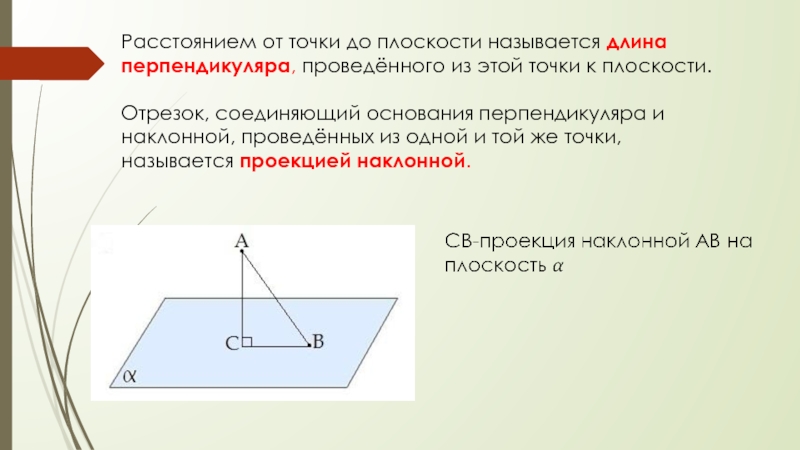
Слайд 8Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой
точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из
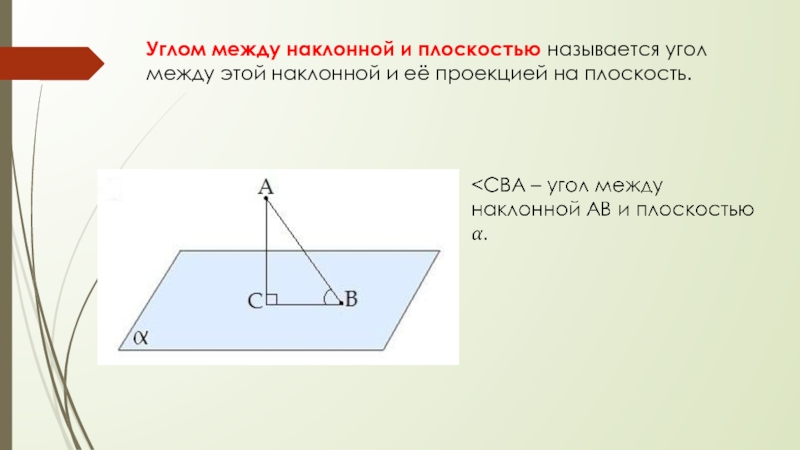
одной и той же точки, называется проекцией наклонной.Слайд 9Углом между наклонной и плоскостью называется угол между этой наклонной и её
проекцией на плоскость.
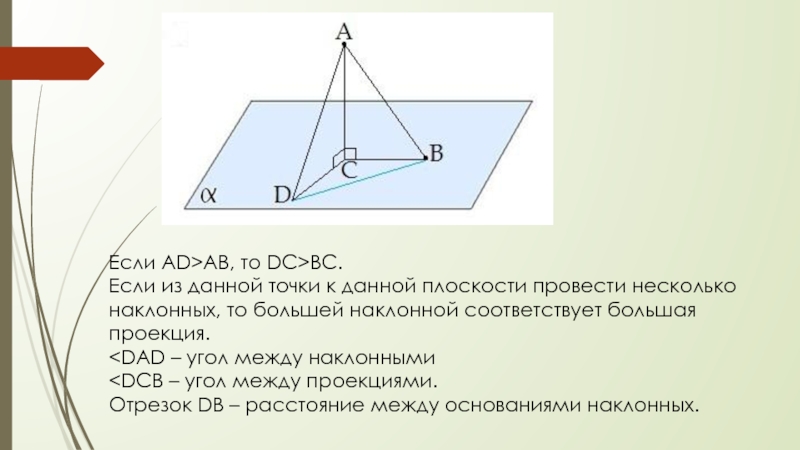
Слайд 10Если AD>АВ, то DC>ВС.
Если из данной точки к данной плоскости
провести несколько наклонных, то большей наклонной соответствует большая проекция.
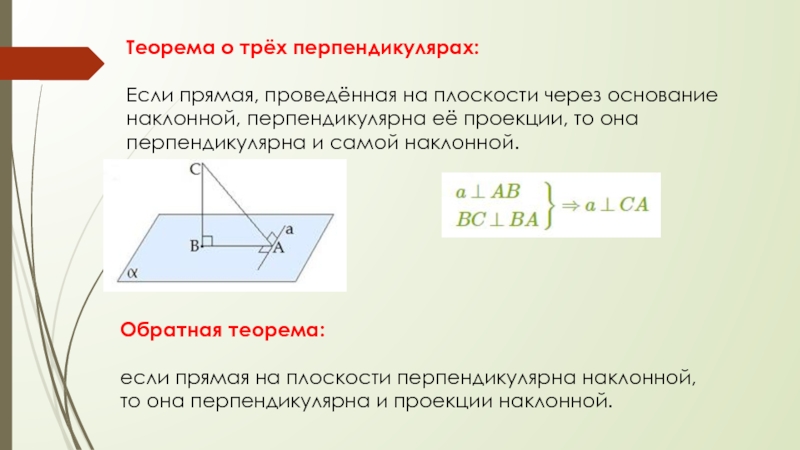
угол между наклоннымиСлайд 11Теорема о трёх перпендикулярах:
Если прямая, проведённая на плоскости через
основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой
наклонной.Обратная теорема:
если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Слайд 13Свойства параллельных плоскостей:
Если две параллельные плоскости пересечены третьей, то линии
их пересечения параллельны.
Отрезки параллельных прямых, заключённые между параллельными плоскостями,
равны.Слайд 14Теорема 1:
Две плоскости параллельны, если одна из них параллельна двум
пересекающимся прямым, лежащим в другой плоскости.
Теорема 2:
Через точку вне данной
плоскости можно провести плоскость параллельную данной, и притом только одну.Теорема 3:
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны
Слайд 15Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими
одну общую границу.
Слайд 16Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла
(аналогично как при пересечении двух прямых получаются четыре угла).
Слайд 17Величина двугранного угла 0
равен 0⸰.
Если при пересечении плоскостей один из двугранных углов составляет
90⸰, то три остальных угла тоже 90⸰.Эти плоскости называют перпендикулярными.
Слайд 18
Теорема 4. Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Теорема 5. Плоскость,
перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.Теорема 6. Если две плоскости перпендикулярны, и в одной из них прямая проведена перпендикулярно линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.