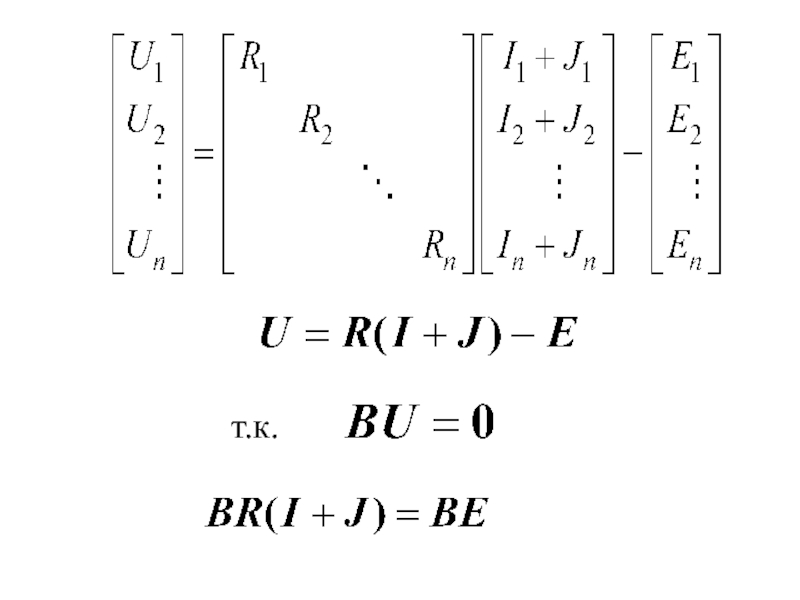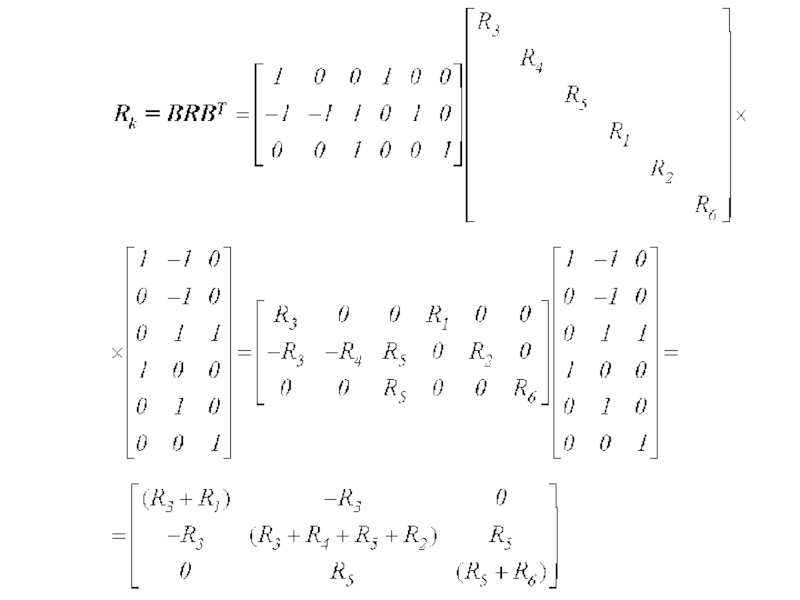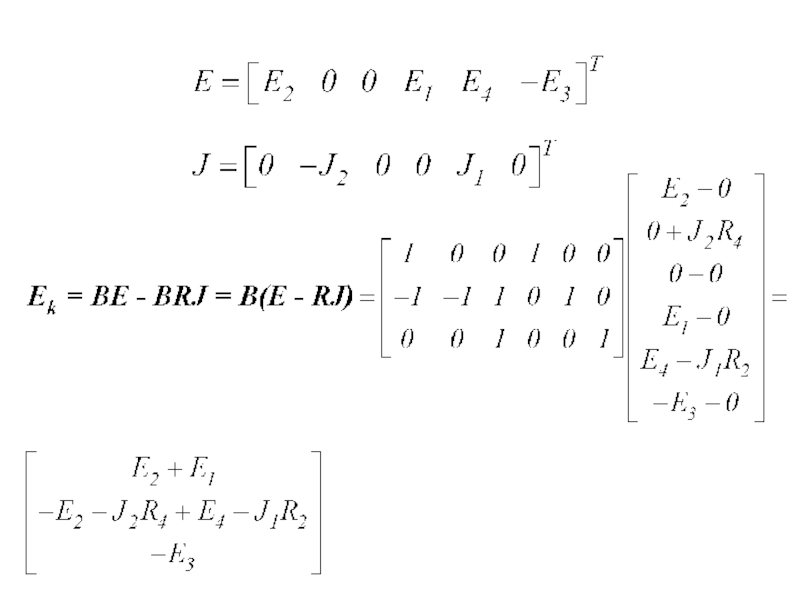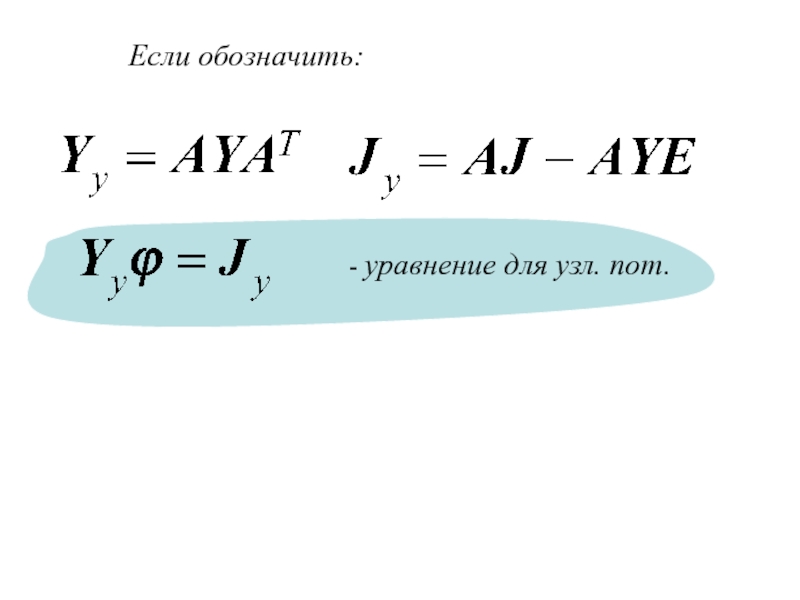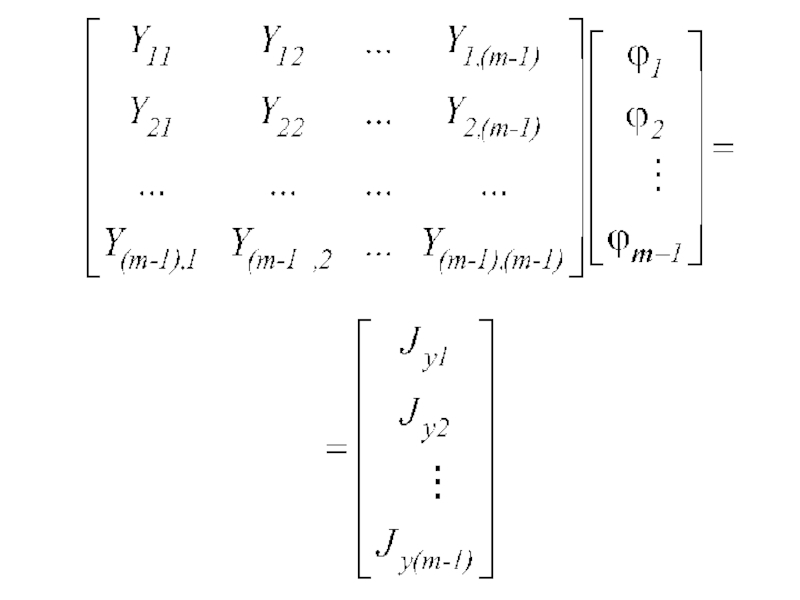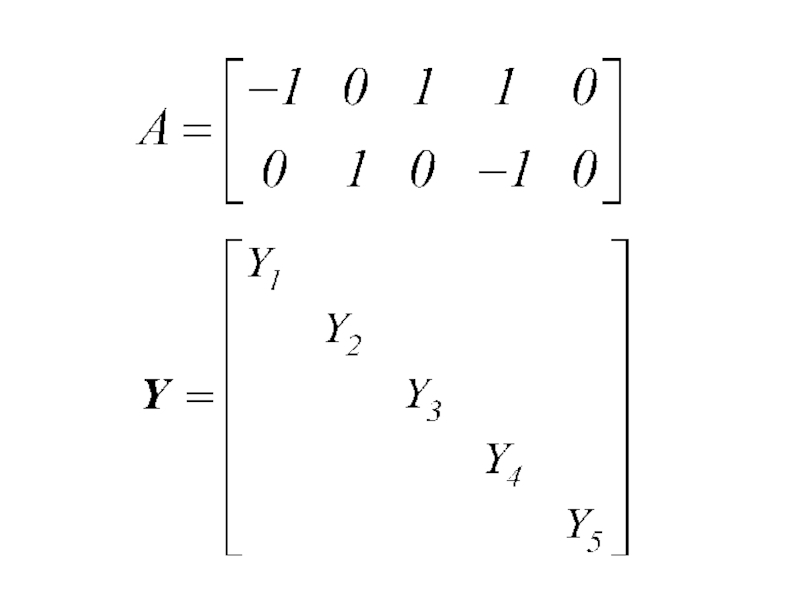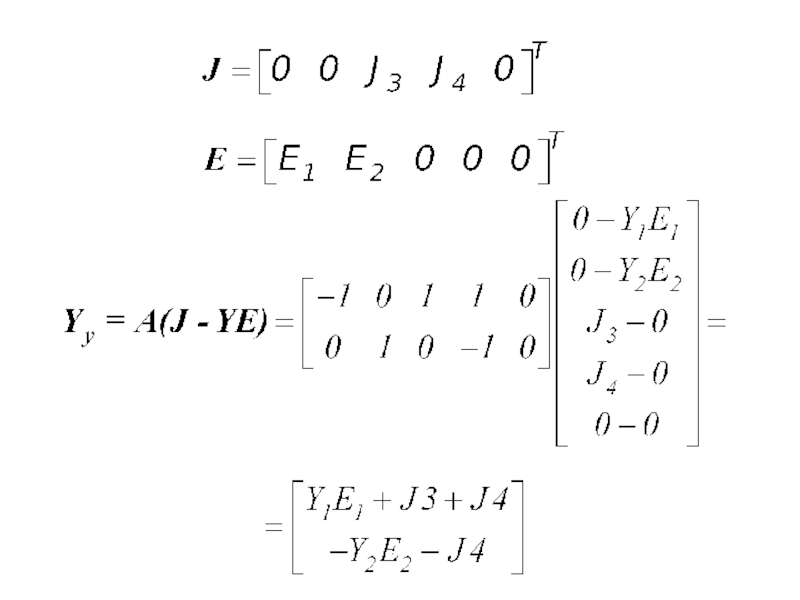Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
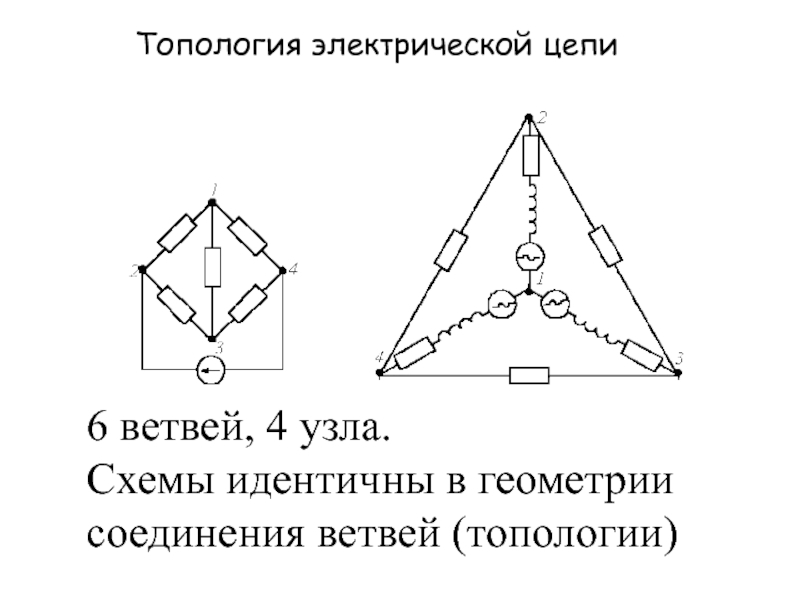
6 ветвей, 4 узла. Схемы идентичны в геометрии соединения ветвей
Содержание
- 1. 6 ветвей, 4 узла. Схемы идентичны в геометрии соединения ветвей
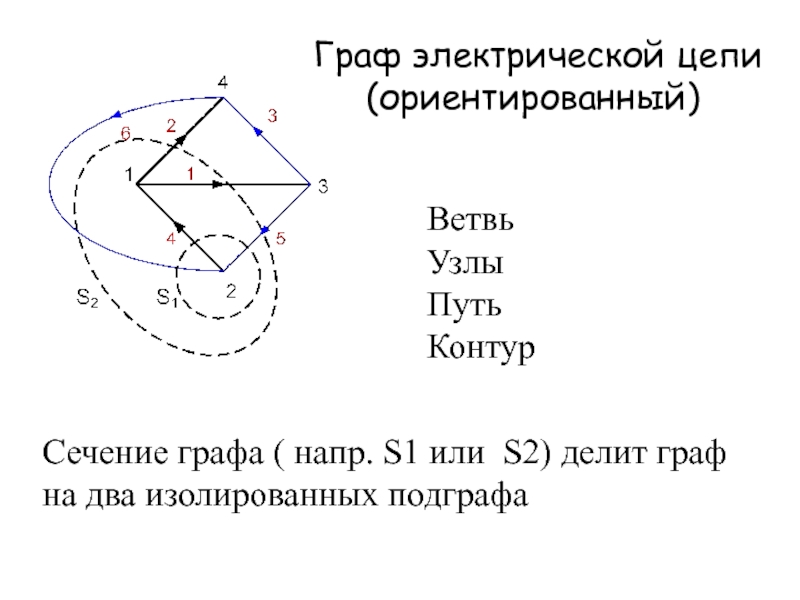
- 2. Граф электрической цепи (ориентированный)ВетвьУзлыПутьКонтурСечение графа
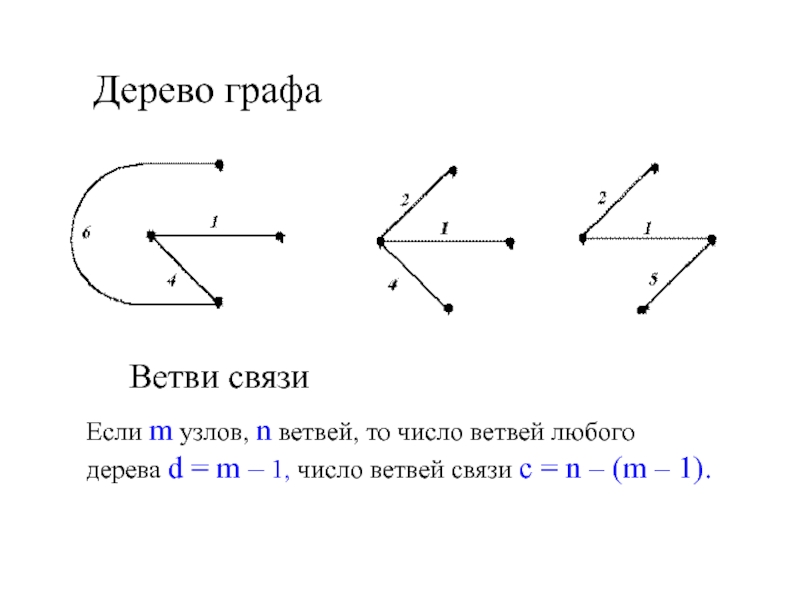
- 3. Дерево графаВетви связиЕсли m узлов, n ветвей,
- 4. Главный контур – ветви дерева и одна
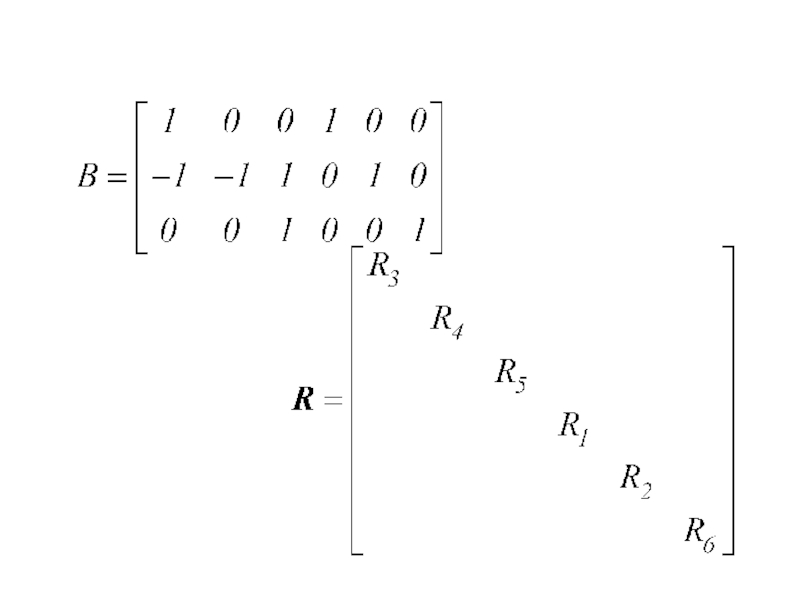
- 5. Узловаяматрица
- 6. Первый закон КирхгофаДля данного графа:
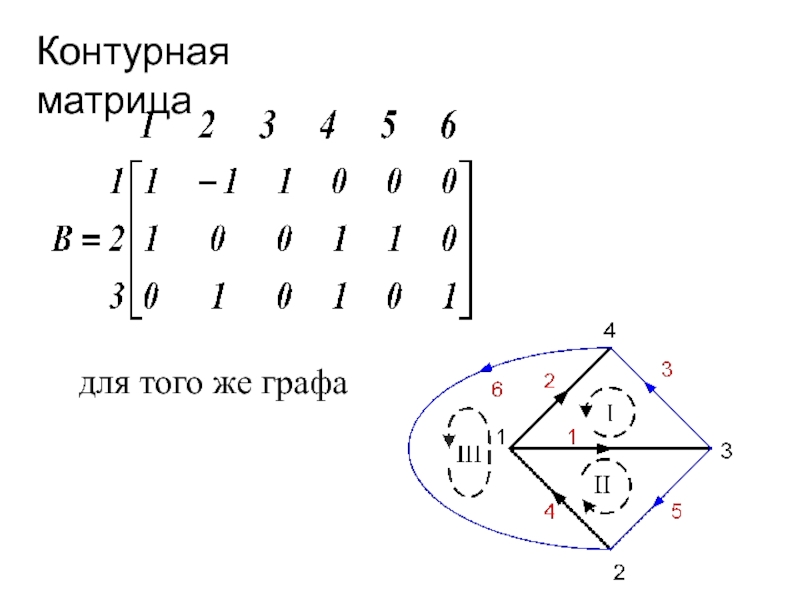
- 7. Контурная матрицадля того же графа
- 8. Для какого-либо контура- (2-й закон Кирхгофа).Введем столбцовую матрицу напряжений ветвей:Тогда в матричной форме:
- 9. Записывается c = (n – m +1)
- 10. Основы матричных методов расчетаЗакон Ома для обобщенной ветви:
- 11. т.к.
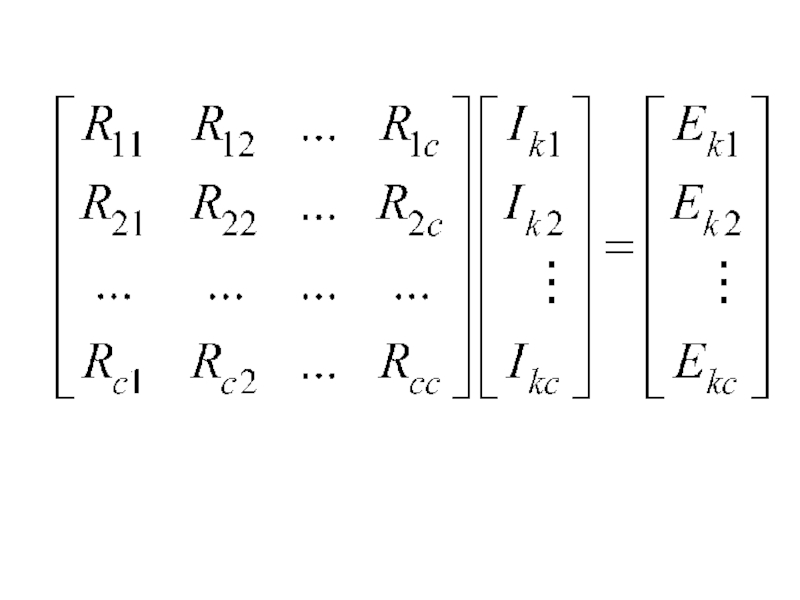
- 12. Метод контурных токов в матричной форме: В
- 13. - матрица конт. сопротивлений- матрица конт. ЭДС-
- 14. Слайд 14
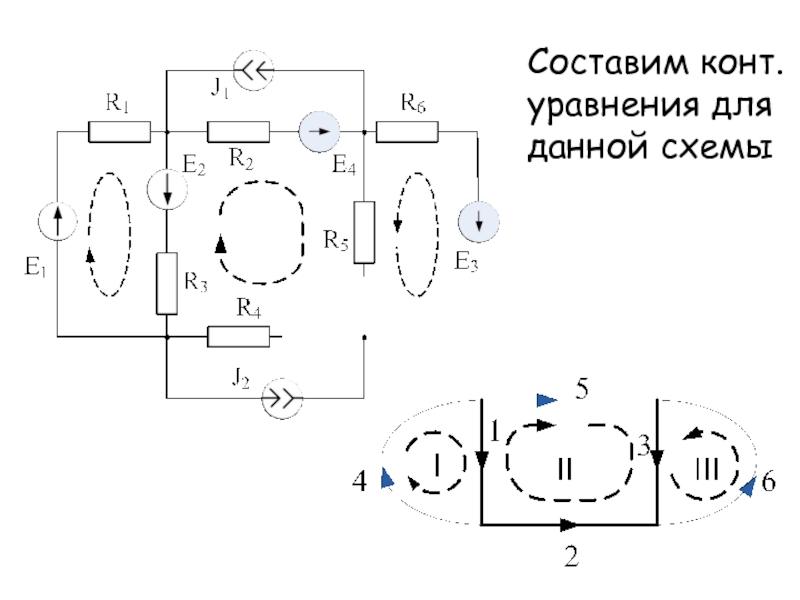
- 15. Составим конт. уравнения для данной схемы
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Окончательно получим:
- 20. Метод узловых потенциалов в матричной формеЗапишем закон Ома в матричной форме относительнотоков в ветвях где
- 21. 1-й закон КирхгофаПодставим м. ст. токов: Для потенциалов узлов (m-1)
- 22. Если обозначить:
- 23. Слайд 23
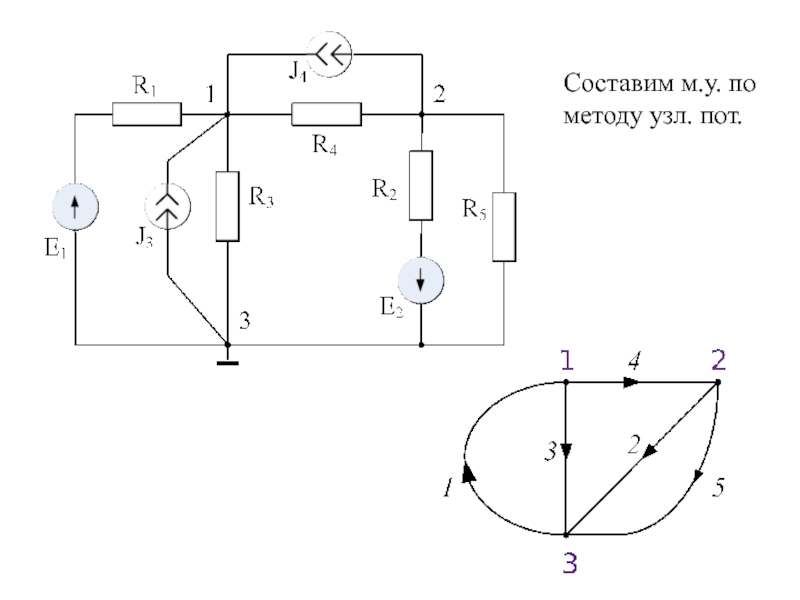
- 24. Составим м.у. пометоду узл. пот.
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Окончательно:
- 29. Скачать презентанцию
Граф электрической цепи (ориентированный)ВетвьУзлыПутьКонтурСечение графа ( напр. S1 или S2) делит граф на два изолированных подграфа
Слайды и текст этой презентации
Слайд 16 ветвей, 4 узла.
Схемы идентичны в геометрии соединения ветвей (топологии)
Топология
электрической цепи
Слайд 2Граф электрической цепи
(ориентированный)
Ветвь
Узлы
Путь
Контур
Сечение графа ( напр. S1
или S2) делит граф
на два изолированных подграфа
Слайд 3Дерево графа
Ветви связи
Если m узлов, n ветвей, то число ветвей
любого
дерева d = m – 1, число ветвей связи
с = n – (m – 1).
Слайд 4Главный контур – ветви дерева и одна ветвь связи.
Топологические матрицы
Узловая
матрица – по 1-му закону Кирхгофа
Контурная матрица – по 2-му
закону.
Слайд 8Для какого-либо контура
- (2-й закон Кирхгофа).
Введем столбцовую матрицу напряжений ветвей:
Тогда
в матричной форме:
Слайд 9Записывается c = (n – m +1) независимых уравнений по
2-му закону Кирхгофа для контуров, отл. хотя бы одной
ветвью
(каждый контур со своей ветвью связи). По 1-му закону – (m – 1) уравнений, тогда имеем
m – 1 + c = n уравнений;
т.к. n – число ветвей схемы, то токи в них
определяются однозначно.
Для рассматриваемого
графа:
Слайд 12Метод контурных токов в матричной форме:
В каждом контуре свой
ток, в ветвях эти токи
складываются. Если В матрица главных
контуров, то контурные токи равны токам в ветвях связи.
Последнее преобразуем:
это матр. столбец (вектор) токов
в ветвях
IK - матр. столбец контурных токов
Слайд 13
- матрица конт. сопротивлений
- матрица конт. ЭДС
- уравнение для конт.
токов
Выражаем I через IK
Слайд 20Метод узловых потенциалов в матричной форме
Запишем закон Ома в матричной
форме относительно
токов в ветвях
где
