Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аберрации
Содержание
- 1. Аберрации
- 2. Определение Разность координат (угловых или линейных) даваемых реальной
- 3. Виды аберраций:Монохроматические (аберрации не зависящие от длины волны света)Хроматические (аберрации зависящие от длины волны света)
- 4. Монохроматические АберрацииСферическая АберрацияКомаАстигматизмКривизна поляДисторсия
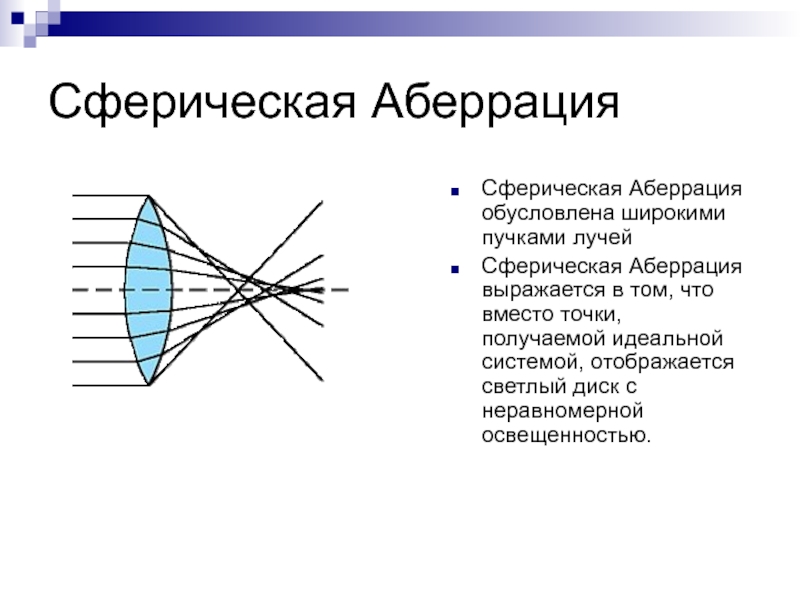
- 5. Сферическая АберрацияСферическая Аберрация обусловлена широкими пучками лучей
- 6. Сферическая аберрацияМерами сферической аберрации являются поперечная и
- 7. Сферическая аберрацияДля частичного исправления сферической аберрации используют комбинацию положительной и отрицательной линз.
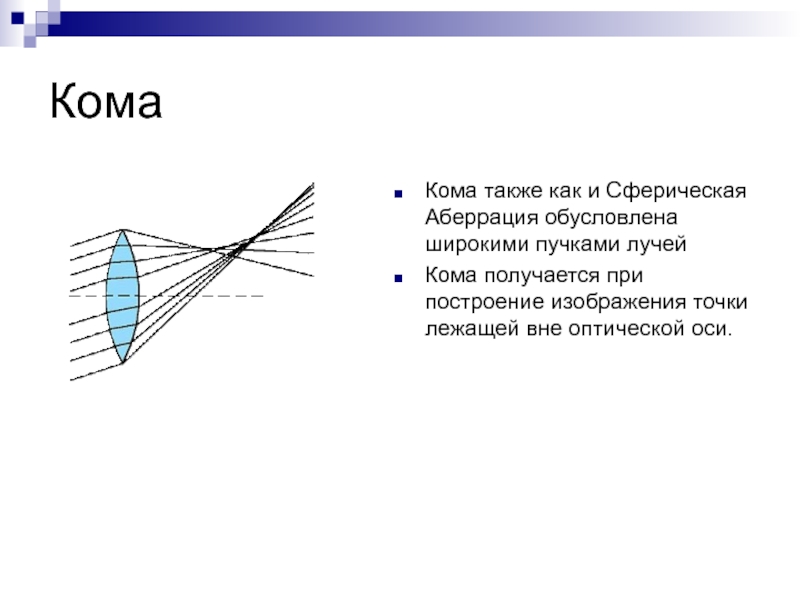
- 8. КомаКома также как и Сферическая Аберрация обусловлена
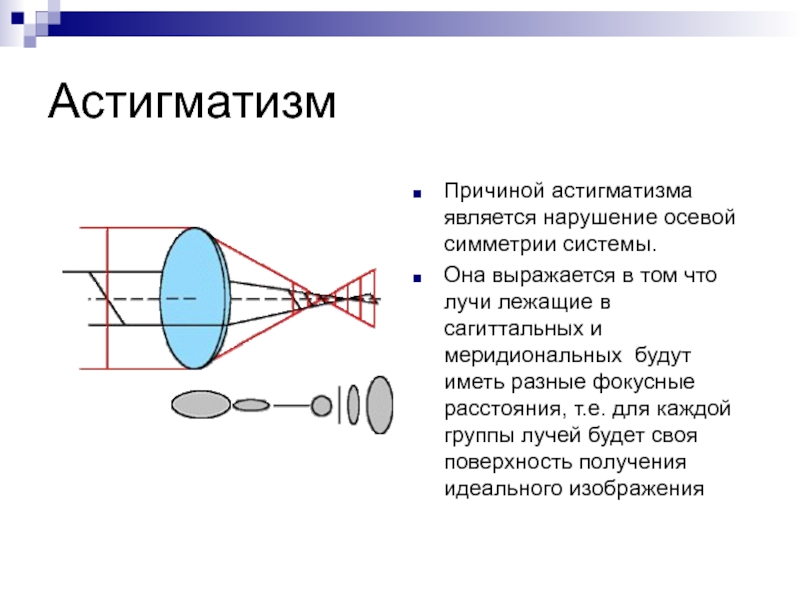
- 9. АстигматизмПричиной астигматизма является нарушение осевой симметрии системы.Она
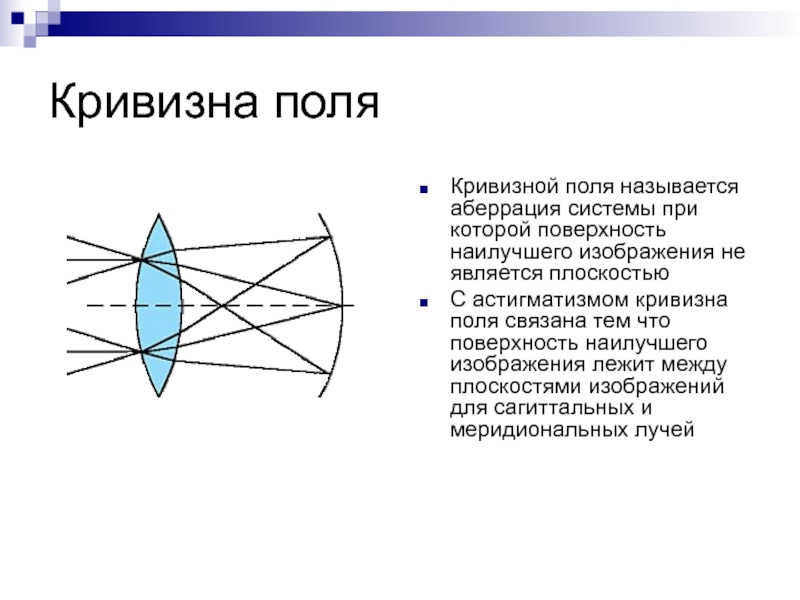
- 10. Кривизна поляКривизной поля называется аберрация системы при
- 11. ДисторсияДисторсия связана с непостоянством линейного увеличения для
- 12. Хроматические аберрацииХроматическая аберрация увеличенияХроматическая аберрация положения
- 13. Хроматические аберрацииХроматическая аберрация связана с дисперсией(зависимостью показателя
- 14. Хроматическая Аберрация положения∆S´хр = S´f + S´s
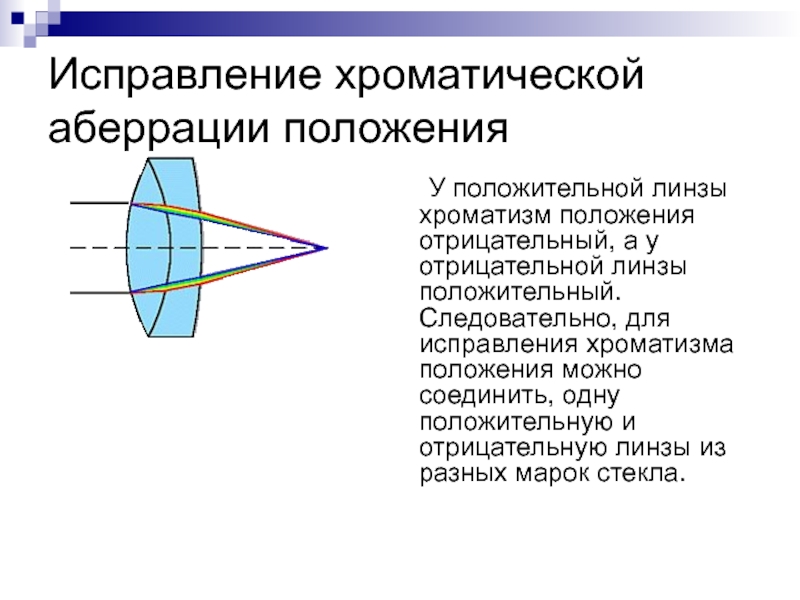
- 15. Исправление хроматической аберрации положения У положительной линзы хроматизм
- 16. Вторичный спектрОптические системы, у которых в одну
- 17. Хроматическая Аберрация увеличенияХроматическая аберрация увеличения состоит в
- 18. Скачать презентанцию
Определение Разность координат (угловых или линейных) даваемых реальной и идеальной оптической системой называют погрешностями или аберрациями оптической системы. Количественно аберрации можно получить сравнив координаты вычисленные по точным тригонометрическим формулам и формулам параксиальной оптики.
Слайды и текст этой презентации
Слайд 2Определение
Разность координат (угловых или линейных) даваемых реальной и идеальной оптической
системой называют погрешностями или аберрациями оптической системы.
сравнив координаты вычисленные по точным тригонометрическим формулам и формулам параксиальной оптики.Слайд 3Виды аберраций:
Монохроматические (аберрации не зависящие от длины волны света)
Хроматические (аберрации
зависящие от длины волны света)
Слайд 5Сферическая Аберрация
Сферическая Аберрация обусловлена широкими пучками лучей
Сферическая Аберрация выражается
в том, что вместо точки, получаемой идеальной системой, отображается светлый
диск с неравномерной освещенностью.Слайд 6Сферическая аберрация
Мерами сферической аберрации являются поперечная и продольная сферические аберрации
Продольной сферическая аберрация по величине равна разности между положением F
(точка получаемая лучами параксиальной области) и F` (точка получаемая крайними лучами линзы)—∆x. Продольная аберрация называется положительной если точка F` лежит правее точки F и отрицательной в обратном случае.Поперечная сферическая аберрация по величине равна разности между положением F (точка получаемая лучами параксиальной области) и положением точки пересечения крайних лучей и плоскости получения параксиального изображения—∆y.
Слайд 7Сферическая аберрация
Для частичного исправления сферической аберрации используют комбинацию положительной и
отрицательной линз.
Слайд 8Кома
Кома также как и Сферическая Аберрация обусловлена широкими пучками лучей
Кома
получается при построение изображения точки лежащей вне оптической оси.
Слайд 9Астигматизм
Причиной астигматизма является нарушение осевой симметрии системы.
Она выражается в том
что лучи лежащие в сагиттальных и меридиональных будут иметь разные
фокусные расстояния, т.е. для каждой группы лучей будет своя поверхность получения идеального изображенияСлайд 10Кривизна поля
Кривизной поля называется аберрация системы при которой поверхность наилучшего
изображения не является плоскостью
С астигматизмом кривизна поля связана тем что
поверхность наилучшего изображения лежит между плоскостями изображений для сагиттальных и меридиональных лучейСлайд 11Дисторсия
Дисторсия связана с непостоянством линейного увеличения для различных углов поля
зрения
Если линейное увеличение возрастает от центра то это подушкообразная дисторсия
Если линейное увеличение уменьшается от центра то это бочкообразная дисторсия
Слайд 13Хроматические аберрации
Хроматическая аберрация связана с дисперсией(зависимостью показателя преломления от длины
волны света). Т.к. фокусное расстояние зависит от показателя преломления, то
для каждой длины волны будет построено свое изображение не совпадающие с остальными.Хроматическая аберрация выражается в появление у изображения цветной каймы у изображения
Слайд 15Исправление хроматической аберрации положения
У положительной линзы хроматизм положения отрицательный, а
у отрицательной линзы положительный. Следовательно, для исправления хроматизма положения можно
соединить, одну положительную и отрицательную линзы из разных марок стекла.Слайд 16Вторичный спектр
Оптические системы, у которых в одну точку соединены точки
изображения для красного и синего цветов, называются ахроматами. Такие систем
еще не дают вполне бесцветного изображения точки на оси, т.е. изображение точек для других волн будут располагаться на различных расстояниях от системы вдоль оптической оси. Такой остаточный хроматизм называется вторичным спектром.Слайд 17Хроматическая Аберрация увеличения
Хроматическая аберрация увеличения состоит в том что линейное
увеличение V меняет свою величину при изменении длины волны света
Хроматическая
аберрация увеличения определяется разностью линейных увеличений для красного C и синего F цветов∆Vхр=Vc – Vf
или разностью величин изображений для тех же цветов
∆y´хр=y´c – y´f