Аксиомы стереометрии Часть 1 Стереометрия Цель: 10.2.1 знать аксиомы

Содержание

1. Аксиомы стереометрии Часть 1 Стереометрия Цель: 10.2.1 знать аксиомы
2. Аксиомы планиметрии Аксиома 1. Какова бы ни
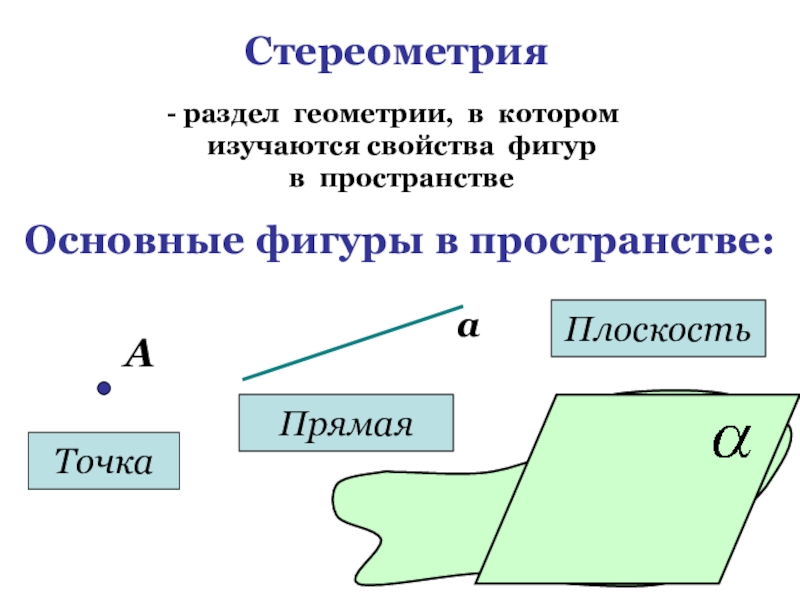
3. Стереометрия раздел геометрии, в котором изучаются свойства фигур в пространствеОсновные фигуры в пространстве:АТочкааПрямаяПлоскость
4. A, B, C, …a, b, c, …илиAВ, BС, CD, …
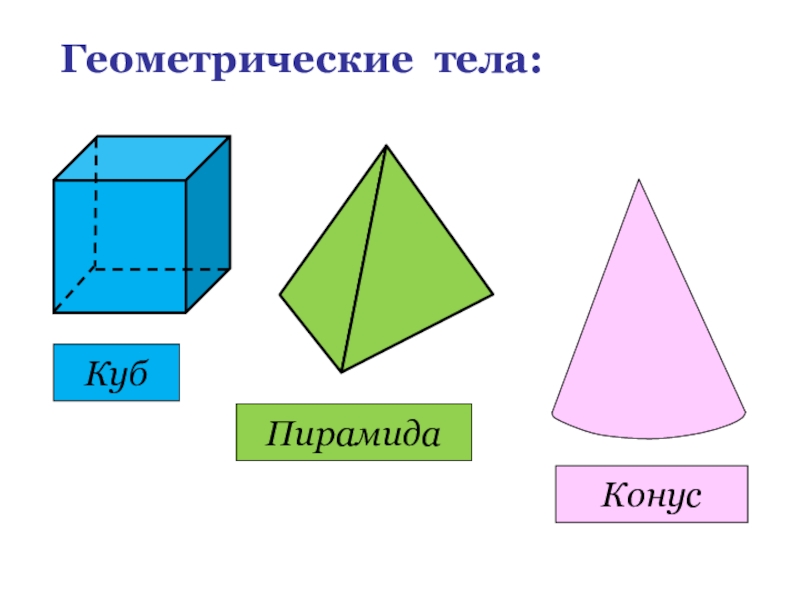
5. Геометрические тела:КубПирамидаКонус
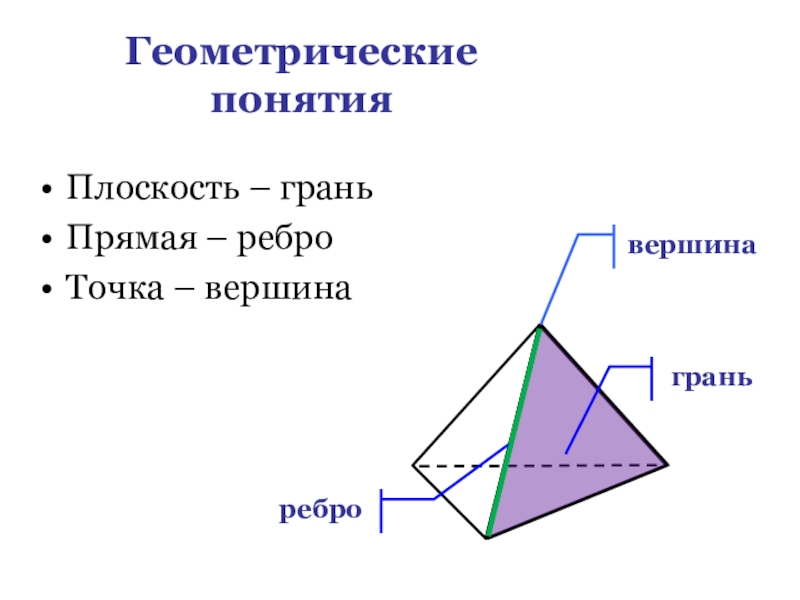
6. Геометрические понятияПлоскость – граньПрямая – реброТочка – вершинавершинаграньребро
7. Стереометрия широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники
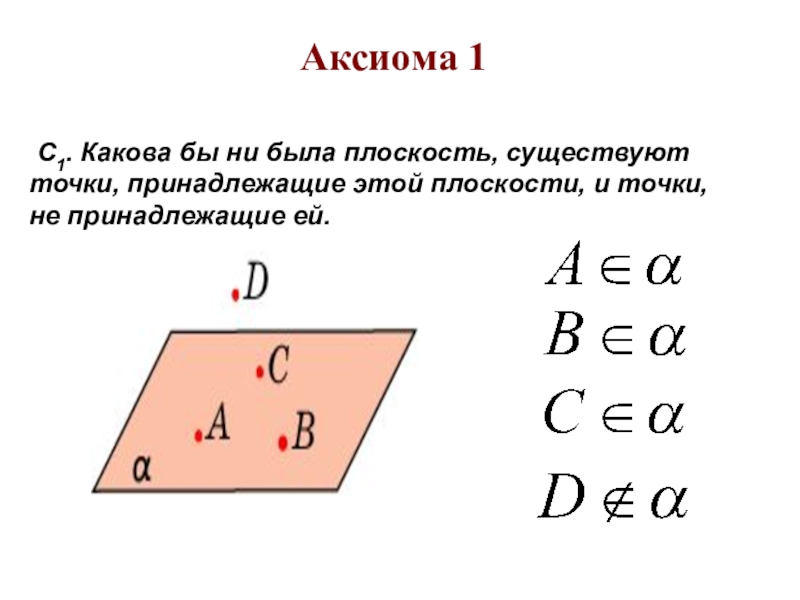
8. Аксиома 1 С1. Какова бы ни была
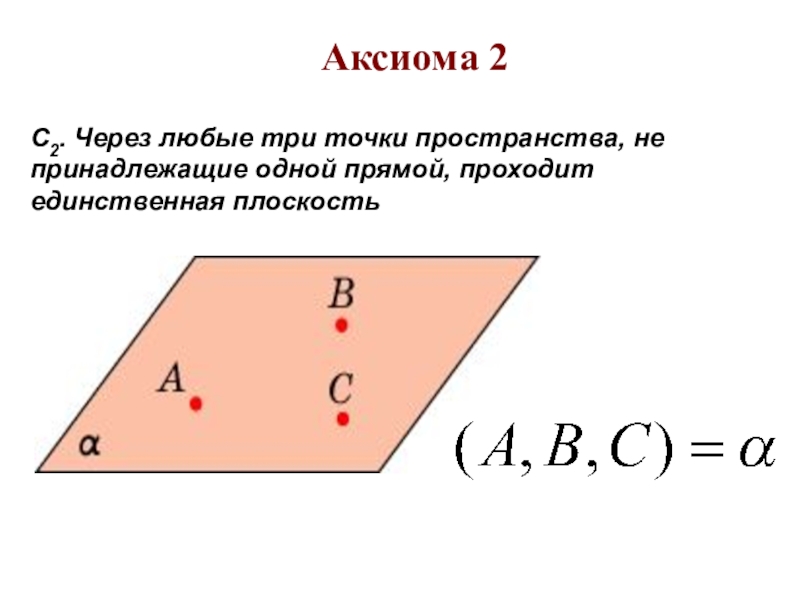
9. С2. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная плоскость Аксиома 2
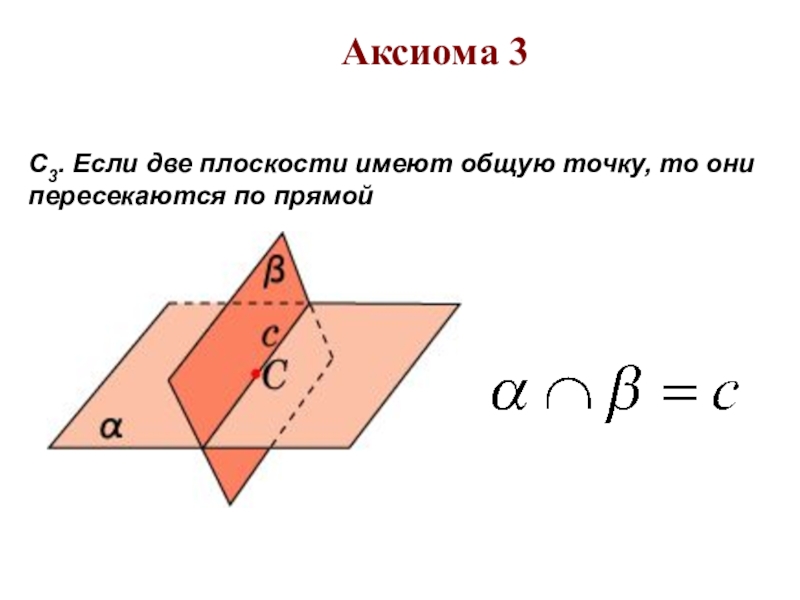
10. С3. Если две плоскости имеют общую точку, то они пересекаются по прямойАксиома 3
11. Слайд 11
12. Слайд 12
13. Скачать презентанцию

Аксиомы планиметрии Аксиома 1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и точки, не принадлежащие ей. Через любые две точки можно провести прямую и только одну.Аксиома 2. Из

Главная
Разное
Аксиомы стереометрии Часть 1 Стереометрия Цель: 10.2.1 знать аксиомы

Слайды и текст этой презентации

Слайд 1
Аксиомы
стереометрии
Часть 1
Стереометрия
Цель: 10.2.1 знать аксиомы стереометрии, их следствия;

иллюстрировать и записывать их с помощью математических символов

АксиомыстереометрииЧасть 1 Стереометрия Цель: 10.2.1 знать аксиомы стереометрии, их следствия; иллюстрировать и записывать их с помощью математических

Слайд 2Аксиомы планиметрии
Аксиома 1. Какова бы ни была прямая, существуют

точки, принадлежащие этой прямой и точки, не принадлежащие ей. Через

любые две точки можно провести прямую и только одну.

Аксиома 2. Из трех точек на прямой одна о только одна лежит между двумя другими.

Аксиома 3. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Аксиома 4. Прямая разбивает плоскость на две полуплоскости.

Аксиома 5. Каждый угол имеет определенную градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиома 6. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

Аксиома 7. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180, и только один.

Аксиома 8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Аксиома 9. Через точку, не лежащую на данной прямой можно провести на плоскости не более одной прямой, параллельной данной.

Аксиома – утверждение, принимаемое без доказательства.
Теорема – утверждение, требующее доказательство.