Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритм RSA
Содержание
- 1. Алгоритм RSA
- 2. Краткий экскурсОпубликованная в ноябре 1976 года статья
- 3. СоздателиИзучив эту статью, трое учёных Рональд Ривест,
- 4. ОпределениеRSA (аббревиатура от фамилий Rivest, Shamir и
- 5. Вычислительная сложность — понятие в информатике и
- 6. ВведениеКриптографические системы с открытым ключом используют так
- 7. ХарактеристикаВ основу криптографической системы с открытым ключом
- 8. Принцип действияВ криптографической системе с открытым ключом
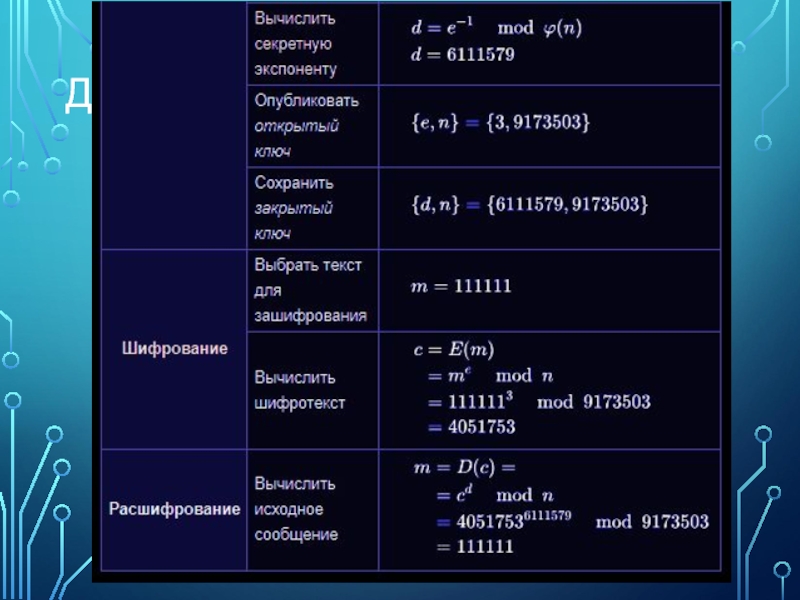
- 9. Пример работы алгоритма
- 10. Дальнейшие шаги
- 11. Применение RSAСистема RSA используется для защиты программного
- 12. Спасибо за внимание
- 13. Скачать презентанцию
Краткий экскурсОпубликованная в ноябре 1976 года статья Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» (англ. New Directions in Cryptography)[5] перевернула представление о криптографических системах, заложив основы криптографии с открытым
Слайды и текст этой презентации
Слайд 3Создатели
Изучив эту статью, трое учёных Рональд Ривест, Ади Шамир и
Леонард Адлеман из Массачусетского технологического института (MIT) приступили к поискам
математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.Слайд 4Определение
RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический
алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации
больших целых чисел.т.е., криптографическая система с открытым ключом — система шифрования и/или электронной подписи (ЭП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для проверки ЭП и для шифрования сообщения. Для генерации ЭП и для расшифровки сообщения используется закрытый ключ.
Слайд 5Вычислительная сложность — понятие в информатике и теории алгоритмов, обозначающее
функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера
входных данных.Факторизацией натурального числа называется его разложение в произведение простых множителей. Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA. Более того, если известен хотя бы один из параметров ключей RSA, то система взламывается однозначно, кроме того, существует множество алгоритмов восстановления всех ключей в системе, обладая какими-то данными.
Слайд 6Введение
Криптографические системы с открытым ключом используют так называемые односторонние функции,
которые обладают следующим свойством:
Если известно x, то f(x) вычислить относительно
просто. Если известно y=f(x), то для вычисления x нет простого (эффективного) пути.Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
Слайд 7Характеристика
В основу криптографической системы с открытым ключом RSA положена сложность
задачи факторизации произведения двух больших простых чисел. Для шифрования используется
операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.Слайд 8Принцип действия
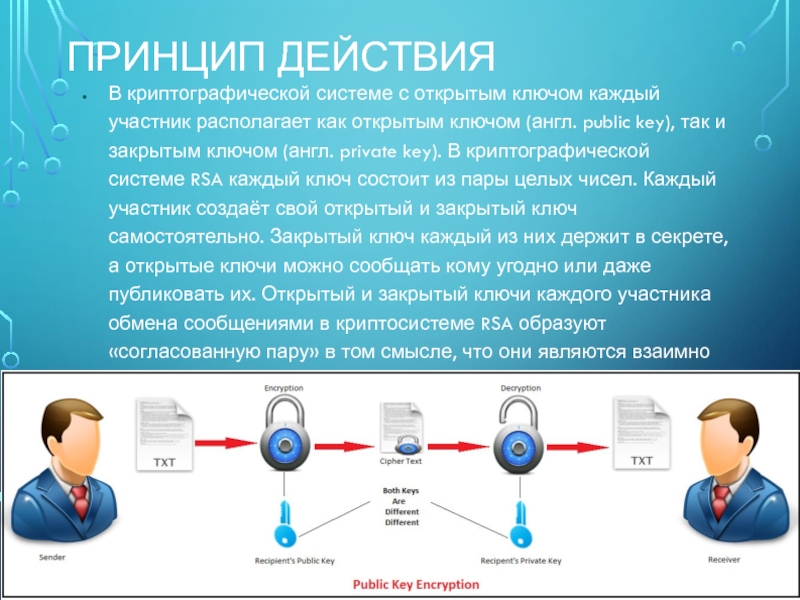
В криптографической системе с открытым ключом каждый участник располагает
как открытым ключом (англ. public key), так и закрытым ключом
(англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными.Слайд 11Применение RSA
Система RSA используется для защиты программного обеспечения и в
схемах цифровой подписи.
Также она используется в открытой системе шифрования PGP
и иных системах шифрования (к примеру, DarkCryptTC и формат xdc) в сочетании с симметричными алгоритмами.Из-за низкой скорости шифрования (около 30 кбит/с при 512-битном ключе на процессоре 2 ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным сеансовым ключом (например, AES, IDEA, Serpent, Twofish), а с помощью RSA шифруют лишь этот ключ, таким образом реализуется гибридная криптосистема. Такой механизм имеет потенциальные уязвимости ввиду необходимости использовать криптографически стойкий генератор псевдослучайных чисел для формирования случайного сеансового ключа симметричного шифрования.